This article may be confusing or unclear to readers. (September 2008) |
| 2D | 3D |
|---|---|
 Truncated triangle or uniform hexagon, with Coxeter diagram |
 Truncated octahedron, |
| 4D | 5D |
 Truncated 16-cell, |
 Truncated 5-orthoplex, |
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons (the definition is different in 2 dimensions to exclude vertex-transitive even-sided polygons that alternate two different lengths of edges).
This is a generalization of the older category of semiregular polytopes, but also includes the regular polytopes. Further, star regular faces and vertex figures (star polygons) are allowed, which greatly expand the possible solutions. A strict definition requires uniform polytopes to be finite, while a more expansive definition allows uniform honeycombs (2-dimensional tilings and higher dimensional honeycombs) of Euclidean and hyperbolic space to be considered polytopes as well.
Operations edit
Nearly every uniform polytope can be generated by a Wythoff construction, and represented by a Coxeter diagram. Notable exceptions include the great dirhombicosidodecahedron in three dimensions and the grand antiprism in four dimensions. The terminology for the convex uniform polytopes used in uniform polyhedron, uniform 4-polytope, uniform 5-polytope, uniform 6-polytope, uniform tiling, and convex uniform honeycomb articles were coined by Norman Johnson.[citation needed]
Equivalently, the Wythoffian polytopes can be generated by applying basic operations to the regular polytopes in that dimension. This approach was first used by Johannes Kepler, and is the basis of the Conway polyhedron notation.
Rectification operators edit
Regular n-polytopes have n orders of rectification. The zeroth rectification is the original form. The (n−1)-th rectification is the dual. A rectification reduces edges to vertices, a birectification reduces faces to vertices, a trirectification reduces cells to vertices, a quadirectification reduces 4-faces to vertices, a quintirectification reduced 5-faces to vertices, and so on.
An extended Schläfli symbol can be used for representing rectified forms, with a single subscript:
- k-th rectification = tk{p1, p2, ..., pn-1} = kr.
Truncation operators edit
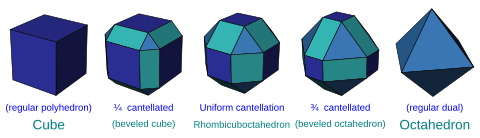
Truncation operations that can be applied to regular n-polytopes in any combination. The resulting Coxeter diagram has two ringed nodes, and the operation is named for the distance between them. Truncation cuts vertices, cantellation cuts edges, runcination cuts faces, sterication cut cells. Each higher operation also cuts lower ones too, so a cantellation also truncates vertices.
- t0,1 or t: Truncation - applied to polygons and higher. A truncation removes vertices, and inserts a new facet in place of each former vertex. Faces are truncated, doubling their edges. (The term, coined by Kepler, comes from Latin truncare 'to cut off'.)
- There are higher truncations also: bitruncation t1,2 or 2t, tritruncation t2,3 or 3t, quadritruncation t3,4 or 4t, quintitruncation t4,5 or 5t, etc.
- t0,2 or rr: Cantellation - applied to polyhedra and higher. It can be seen as rectifying its rectification. A cantellation truncates both vertices and edges and replaces them with new facets. Cells are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from the verb cant, like bevel, meaning to cut with a slanted face.)
- There are higher cantellations also: bicantellation t1,3 or r2r, tricantellation t2,4 or r3r, quadricantellation t3,5 or r4r, etc.
- t0,1,2 or tr: Cantitruncation - applied to polyhedra and higher. It can be seen as truncating its rectification. A cantitruncation truncates both vertices and edges and replaces them with new facets. Cells are replaced by topologically expanded copies of themselves. (The composite term combines cantellation and truncation)
- There are higher cantellations also: bicantitruncation t1,2,3 or t2r, tricantitruncation t2,3,4 or t3r, quadricantitruncation t3,4,5 or t4r, etc.
- t0,3: Runcination - applied to Uniform 4-polytope and higher. Runcination truncates vertices, edges, and faces, replacing them each with new facets. 4-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Latin runcina 'carpenter's plane'.)
- There are higher runcinations also: biruncination t1,4, triruncination t2,5, etc.
- t0,4 or 2r2r: Sterication - applied to Uniform 5-polytopes and higher. It can be seen as birectifying its birectification. Sterication truncates vertices, edges, faces, and cells, replacing each with new facets. 5-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Greek stereos 'solid'.)
- There are higher sterications also: bisterication t1,5 or 2r3r, tristerication t2,6 or 2r4r, etc.
- t0,2,4 or 2t2r: Stericantellation - applied to Uniform 5-polytopes and higher. It can be seen as bitruncating its birectification.
- There are higher sterications also: bistericantellation t1,3,5 or 2t3r, tristericantellation t2,4,6 or 2t4r, etc.
- t0,5: Pentellation - applied to Uniform 6-polytopes and higher. Pentellation truncates vertices, edges, faces, cells, and 4-faces, replacing each with new facets. 6-faces are replaced by topologically expanded copies of themselves. (Pentellation is derived from Greek pente 'five'.)
- There are also higher pentellations: bipentellation t1,6, tripentellation t2,7, etc.
- t0,6 or 3r3r: Hexication - applied to Uniform 7-polytopes and higher. It can be seen as trirectifying its trirectification. Hexication truncates vertices, edges, faces, cells, 4-faces, and 5-faces, replacing each with new facets. 7-faces are replaced by topologically expanded copies of themselves. (Hexication is derived from Greek hex 'six'.)
- There are higher hexications also: bihexication: t1,7 or 3r4r, trihexication: t2,8 or 3r5r, etc.
- t0,3,6 or 3t3r: Hexiruncinated - applied to Uniform 7-polytopes and higher. It can be seen as tritruncating its trirectification.
- There are also higher hexiruncinations: bihexiruncinated: t1,4,7 or 3t4r, trihexiruncinated: t2,5,8 or 3t5r, etc.
- t0,7: Heptellation - applied to Uniform 8-polytopes and higher. Heptellation truncates vertices, edges, faces, cells, 4-faces, 5-faces, and 6-faces, replacing each with new facets. 8-faces are replaced by topologically expanded copies of themselves. (Heptellation is derived from Greek hepta 'seven'.)
- There are higher heptellations also: biheptellation t1,8, triheptellation t2,9, etc.
- t0,8 or 4r4r: Octellation - applied to Uniform 9-polytopes and higher.
- t0,9: Ennecation - applied to Uniform 10-polytopes and higher.
In addition combinations of truncations can be performed which also generate new uniform polytopes. For example, a runcitruncation is a runcination and truncation applied together.
If all truncations are applied at once, the operation can be more generally called an omnitruncation.
Alternation edit

One special operation, called alternation, removes alternate vertices from a polytope with only even-sided faces. An alternated omnitruncated polytope is called a snub.
The resulting polytopes always can be constructed, and are not generally reflective, and also do not in general have uniform polytope solutions.
The set of polytopes formed by alternating the hypercubes are known as demicubes. In three dimensions, this produces a tetrahedron; in four dimensions, this produces a 16-cell, or demitesseract.
Vertex figure edit
Uniform polytopes can be constructed from their vertex figure, the arrangement of edges, faces, cells, etc. around each vertex. Uniform polytopes represented by a Coxeter diagram, marking active mirrors by rings, have reflectional symmetry, and can be simply constructed by recursive reflections of the vertex figure.
A smaller number of nonreflectional uniform polytopes have a single vertex figure but are not repeated by simple reflections. Most of these can be represented with operations like alternation of other uniform polytopes.
Vertex figures for single-ringed Coxeter diagrams can be constructed from the diagram by removing the ringed node, and ringing neighboring nodes. Such vertex figures are themselves vertex-transitive.
Multiringed polytopes can be constructed by a slightly more complicated construction process, and their topology is not a uniform polytope. For example, the vertex figure of a truncated regular polytope (with 2 rings) is a pyramid. An omnitruncated polytope (all nodes ringed) will always have an irregular simplex as its vertex figure.
Circumradius edit
Uniform polytopes have equal edge-lengths, and all vertices are an equal distance from the center, called the circumradius.
Uniform polytopes whose circumradius is equal to the edge length can be used as vertex figures for uniform honeycombs. For example, the regular hexagon divides into 6 equilateral triangles and is the vertex figure for the regular triangular tiling. Also the cuboctahedron divides into 8 regular tetrahedra and 6 square pyramids (half octahedron), and it is the vertex figure for the alternated cubic honeycomb.
Uniform polytopes by dimension edit
It is useful to classify the uniform polytopes by dimension. This is equivalent to the number of nodes on the Coxeter diagram, or the number of hyperplanes in the Wythoffian construction. Because (n+1)-dimensional polytopes are tilings of n-dimensional spherical space, tilings of n-dimensional Euclidean and hyperbolic space are also considered to be (n+1)-dimensional. Hence, the tilings of two-dimensional space are grouped with the three-dimensional solids.
One dimension edit
The only one-dimensional polytope is the line segment. It corresponds to the Coxeter family A1.
Two dimensions edit
In two dimensions, there is an infinite family of convex uniform polytopes, the regular polygons, the simplest being the equilateral triangle. Truncated regular polygons become bicolored geometrically quasiregular polygons of twice as many sides, t{p}={2p}. The first few regular polygons (and quasiregular forms) are displayed below:
| Name | Triangle (2-simplex) |
Square (2-orthoplex) (2-cube) |
Pentagon | Hexagon | Heptagon | Octagon | Enneagon | Decagon | Hendecagon |
|---|---|---|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} t{2} |
{5} | {6} t{3} |
{7} | {8} t{4} |
{9} | {10} t{5} |
{11} |
| Coxeter diagram |
|||||||||
| Image | 
|
 
|
|
 
|

|
|

|
|
|
| Name | Dodecagon | Tridecagon | Tetradecagon | Pentadecagon | Hexadecagon | Heptadecagon | Octadecagon | Enneadecagon | Icosagon |
| Schläfli | {12} t{6} |
{13} | {14} t{7} |
{15} | {16} t{8} |
{17} | {18} t{9} |
{19} | {20} t{10} |
| Coxeter diagram |
|||||||||
| Image |  
|
|
 
|

|
|
|
|
|
 
|
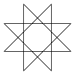
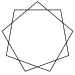
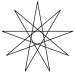
There is also an infinite set of star polygons (one for each rational number greater than 2), but these are non-convex. The simplest example is the pentagram, which corresponds to the rational number 5/2. Regular star polygons, {p/q}, can be truncated into semiregular star polygons, t{p/q}=t{2p/q}, but become double-coverings if q is even. A truncation can also be made with a reverse orientation polygon t{p/(p-q)}={2p/(p-q)}, for example t{5/3}={10/3}.
| Name | Pentagram | Heptagrams | Octagram | Enneagrams | Decagram | ...n-agrams | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} t{4/3} |
{9/2} | {9/4} | {10/3} t{5/3} |
{p/q} |
| Coxeter diagram |
||||||||
| Image | 
|

|

|
|
|
|
 
|
|
Regular polygons, represented by Schläfli symbol {p} for a p-gon. Regular polygons are self-dual, so the rectification produces the same polygon. The uniform truncation operation doubles the sides to {2p}. The snub operation, alternating the truncation, restores the original polygon {p}. Thus all uniform polygons are also regular. The following operations can be performed on regular polygons to derive the uniform polygons, which are also regular polygons:
| Operation | Extended Schläfli Symbols |
Regular result |
Coxeter diagram |
Position | Symmetry | ||
|---|---|---|---|---|---|---|---|
| (1) | (0) | ||||||
| Parent | {p} | t0{p} | {p} | {} | -- | [p] (order 2p) | |
| Rectified (Dual) |
r{p} | t1{p} | {p} | -- | {} | [p] (order 2p) | |
| Truncated | t{p} | t0,1{p} | {2p} | {} | {} | [[p]]=[2p] (order 4p) | |
| Half | h{2p} | {p} | -- | -- | [1+,2p]=[p] (order 2p) | ||
| Snub | s{p} | {p} | -- | -- | [[p]]+=[p] (order 2p) | ||
Three dimensions edit
In three dimensions, the situation gets more interesting. There are five convex regular polyhedra, known as the Platonic solids:
| Name | Schläfli {p,q} |
Diagram |
Image (transparent) |
Image (solid) |
Image (sphere) |
Faces {p} |
Edges | Vertices {q} |
Symmetry | Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedron (3-simplex) (Pyramid) |
{3,3} | 
|

|

|
4 {3} |
6 | 4 {3} |
Td | (self) | |
| Cube (3-cube) (Hexahedron) |
{4,3} | 
|

|

|
6 {4} |
12 | 8 {3} |
Oh | Octahedron | |
| Octahedron (3-orthoplex) |
{3,4} | 
|

|

|
8 {3} |
12 | 6 {4} |
Oh | Cube | |
| Dodecahedron | {5,3} | 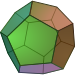
|

|
|
12 {5} |
30 | 20 {3}2 |
Ih | Icosahedron | |
| Icosahedron | {3,5} | 
|

|

|
20 {3} |
30 | 12 {5} |
Ih | Dodecahedron |
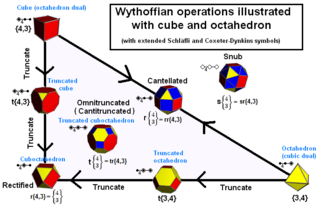
In addition to these, there are also 13 semiregular polyhedra, or Archimedean solids, which can be obtained via Wythoff constructions, or by performing operations such as truncation on the Platonic solids, as demonstrated in the following table:
| Parent | Truncated | Rectified | Bitruncated (tr. dual) |
Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub | |
|---|---|---|---|---|---|---|---|---|
| Tetrahedral 3-3-2 |
 {3,3} |
 (3.6.6) |
 (3.3.3.3) |
 (3.6.6) |
 {3,3} |
 (3.4.3.4) |
 (4.6.6) |
 (3.3.3.3.3) |
| Octahedral 4-3-2 |
 {4,3} |
 (3.8.8) |
 (3.4.3.4) |
 (4.6.6) |
 {3,4} |
 (3.4.4.4) |
 (4.6.8) |
 (3.3.3.3.4) |
| Icosahedral 5-3-2 |
 {5,3} |
 (3.10.10) |
 (3.5.3.5) |
 (5.6.6) |
 {3,5} |
 (3.4.5.4) |
 (4.6.10) |
 (3.3.3.3.5) |
There is also the infinite set of prisms, one for each regular polygon, and a corresponding set of antiprisms.
| # | Name | Picture | Tiling | Vertex figure |
Diagram and Schläfli symbols |
|---|---|---|---|---|---|
| P2p | Prism | 
|

|

|
tr{2,p} |
| Ap | Antiprism | 
|

|

|
sr{2,p} |
The uniform star polyhedra include a further 4 regular star polyhedra, the Kepler-Poinsot polyhedra, and 53 semiregular star polyhedra. There are also two infinite sets, the star prisms (one for each star polygon) and star antiprisms (one for each rational number greater than 3/2).
Constructions edit
The Wythoffian uniform polyhedra and tilings can be defined by their Wythoff symbol, which specifies the fundamental region of the object. An extension of Schläfli notation, also used by Coxeter, applies to all dimensions; it consists of the letter 't', followed by a series of subscripted numbers corresponding to the ringed nodes of the Coxeter diagram, and followed by the Schläfli symbol of the regular seed polytope. For example, the truncated octahedron is represented by the notation: t0,1{3,4}.
| Operation | Schläfli Symbol |
Coxeter diagram |
Wythoff symbol |
Position: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parent | {p,q} | t0{p,q} | q | 2 p | {p} | { } | -- | -- | -- | { } | ||||
| Birectified (or dual) |
{q,p} | t2{p,q} | p | 2 q | -- | { } | {q} | { } | -- | -- | ||||
| Truncated | t{p,q} | t0,1{p,q} | 2 q | p | {2p} | { } | {q} | -- | { } | { } | ||||
| Bitruncated (or truncated dual) |
t{q,p} | t1,2{p,q} | 2 p | q | {p} | { } | {2q} | { } | { } | -- | ||||
| Rectified | r{p,q} | t1{p,q} | 2 | p q | {p} | -- | {q} | -- | { } | -- | ||||
| Cantellated (or expanded) |
rr{p,q} | t0,2{p,q} | p q | 2 | {p} | { }×{ } | {q} | { } | -- | { } | ||||
| Cantitruncated (or Omnitruncated) |
tr{p,q} | t0,1,2{p,q} | 2 p q | | {2p} | { }×{} | {2q} | { } | { } | { } | ||||
| Operation | Schläfli Symbol |
Coxeter diagram |
Wythoff symbol |
Position: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Snub rectified | sr{p,q} | | 2 p q | {p} | {3} {3} |
{q} | -- | -- | -- | |||||
| Snub | s{p,2q} | ht0,1{p,q} | s{2p} | {3} | {q} | -- | {3} | ||||||
|
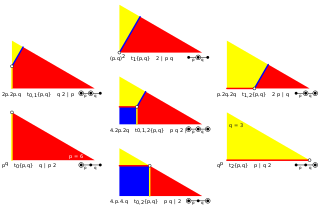 Generating triangles |
Four dimensions edit
In four dimensions, there are 6 convex regular 4-polytopes, 17 prisms on the Platonic and Archimedean solids (excluding the cube-prism, which has already been counted as the tesseract), and two infinite sets: the prisms on the convex antiprisms, and the duoprisms. There are also 41 convex semiregular 4-polytope, including the non-Wythoffian grand antiprism and the snub 24-cell. Both of these special 4-polytope are composed of subgroups of the vertices of the 600-cell.
The four-dimensional uniform star polytopes have not all been enumerated. The ones that have include the 10 regular star (Schläfli-Hess) 4-polytopes and 57 prisms on the uniform star polyhedra, as well as three infinite families: the prisms on the star antiprisms, the duoprisms formed by multiplying two star polygons, and the duoprisms formed by multiplying an ordinary polygon with a star polygon. There is an unknown number of 4-polytope that do not fit into the above categories; over one thousand have been discovered so far.

There are 3 right dihedral angles (2 intersecting perpendicular mirrors):
Edges 1 to 2, 0 to 2, and 1 to 3.

Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional hyperplane, but it is more convenient for our purposes to consider only its two-dimensional intersection with the three-dimensional surface of the hypersphere; thus the mirrors form an irregular tetrahedron.
Each of the sixteen regular 4-polytopes is generated by one of four symmetry groups, as follows:
- group [3,3,3]: the 5-cell {3,3,3}, which is self-dual;
- group [3,3,4]: 16-cell {3,3,4} and its dual tesseract {4,3,3};
- group [3,4,3]: the 24-cell {3,4,3}, self-dual;
- group [3,3,5]: 600-cell {3,3,5}, its dual 120-cell {5,3,3}, and their ten regular stellations.
- group [31,1,1]: contains only repeated members of the [3,3,4] family.
(The groups are named in Coxeter notation.)
Eight of the convex uniform honeycombs in Euclidean 3-space are analogously generated from the cubic honeycomb {4,3,4}, by applying the same operations used to generate the Wythoffian uniform 4-polytopes.
For a given symmetry simplex, a generating point may be placed on any of the four vertices, 6 edges, 4 faces, or the interior volume. On each of these 15 elements there is a point whose images, reflected in the four mirrors, are the vertices of a uniform 4-polytope.
The extended Schläfli symbols are made by a t followed by inclusion of one to four subscripts 0,1,2,3. If there is one subscript, the generating point is on a corner of the fundamental region, i.e. a point where three mirrors meet. These corners are notated as
- 0: vertex of the parent 4-polytope (center of the dual's cell)
- 1: center of the parent's edge (center of the dual's face)
- 2: center of the parent's face (center of the dual's edge)
- 3: center of the parent's cell (vertex of the dual)
(For the two self-dual 4-polytopes, "dual" means a similar 4-polytope in dual position.) Two or more subscripts mean that the generating point is between the corners indicated.
Constructive summary edit
The 15 constructive forms by family are summarized below. The self-dual families are listed in one column, and others as two columns with shared entries on the symmetric Coxeter diagrams. The final 10th row lists the snub 24-cell constructions. This includes all nonprismatic uniform 4-polytopes, except for the non-Wythoffian grand antiprism, which has no Coxeter family.
Truncated forms edit
The following table defines all 15 forms. Each trunction[check spelling] form can have from one to four cell types, located in positions 0,1,2,3 as defined above. The cells are labeled by polyhedral truncation notation.
- An n-gonal prism is represented as : {n}×{ }.
- The green background is shown on forms that are equivalent to either the parent or the dual.
- The red background shows the truncations of the parent, and blue the truncations of the dual.
| Operation | Schläfli symbol | Coxeter diagram |
Cells by position: | ||||
|---|---|---|---|---|---|---|---|
| (3) |
(2) |
(1) |
(0) | ||||
| Parent | {p,q,r} | t0{p,q,r} | {p,q} |
-- |
-- |
-- | |
| Rectified | r{p,q,r} | t1{p,q,r} | r{p,q} |
-- |
-- |
{q,r} | |
| Birectified (or rectified dual) |
2r{p,q,r} = r{r,q,p} |
t2{p,q,r} | {q,p} |
-- |
-- |
r{q,r} | |
| Trirectifed (or dual) |
3r{p,q,r} = {r,q,p} |
t3{p,q,r} | -- |
-- |
-- |
{r,q} | |
| Truncated | t{p,q,r} | t0,1{p,q,r} | t{p,q} |
-- |
-- |
{q,r} | |
| Bitruncated | 2t{p,q,r} | 2t{p,q,r} | t{q,p} |
-- |
-- |
t{q,r} | |
| Tritruncated (or truncated dual) |
3t{p,q,r} = t{r,q,p} |
t2,3{p,q,r} | {q,p} |
-- |
-- |
t{r,q} | |
| Cantellated | rr{p,q,r} | t0,2{p,q,r} | rr{p,q} |
-- |
{ }×{r} |
r{q,r} | |
| Bicantellated (or cantellated dual) |
r2r{p,q,r} = rr{r,q,p} |
t1,3{p,q,r} | r{p,q} |
{p}×{ } |
-- |
rr{q,r} | |
| Runcinated (or expanded) |
e{p,q,r} | t0,3{p,q,r} | {p,q} |
{p}×{ } |
{ }×{r} |
{r,q} | |
| Cantitruncated | tr{p,q,r} | tr{p,q,r} | tr{p,q} |
-- |
{ }×{r} |
t{q,r} | |
| Bicantitruncated (or cantitruncated dual) |
t2r{p,q,r} = tr{r,q,p} |
t1,2,3{p,q,r} | t{q,p} |
{p}×{ } |
-- |
tr{q,r} | |
| Runcitruncated | et{p,q,r} | t0,1,3{p,q,r} | t{p,q} |
{2p}×{ } |
{ }×{r} |
rr{q,r} | |
| Runcicantellated (or runcitruncated dual) |
e3t{p,q,r} = et{r,q,p} |
t0,2,3{p,q,r} | tr{p,q} |
{p}×{ } |
{ }×{2r} |
t{r,q} | |
| Runcicantitruncated (or omnitruncated) |
o{p,q,r} | t0,1,2,3{p,q,r} | tr{p,q} |
{2p}×{ } |
{ }×{2r} |
tr{q,r} | |
Half forms edit
Half constructions exist with holes rather than ringed nodes. Branches neighboring holes and inactive nodes must be even-order. Half construction have the vertices of an identically ringed construction.
| Operation | Schläfli symbol | Coxeter diagram |
Cells by position: | ||||
|---|---|---|---|---|---|---|---|
| (3) |
(2) |
(1) |
(0) | ||||
| Half Alternated |
h{p,2q,r} | ht0{p,2q,r} | h{p,2q} |
-- |
-- |
-- | |
| Alternated rectified | hr{2p,2q,r} | ht1{2p,2q,r} | hr{2p,2q} |
-- |
-- |
h{2q,r} | |
| Snub Alternated truncation |
s{p,2q,r} | ht0,1{p,2q,r} | s{p,2q} |
-- |
-- |
h{2q,r} | |
| Bisnub Alternated bitruncation |
2s{2p,q,2r} | ht1,2{2p,q,2r} | s{q,2p} |
-- |
-- |
s{q,2r} | |
| Snub rectified Alternated truncated rectified |
sr{p,q,2r} | ht0,1,2{p,q,2r} | sr{p,q} |
-- |
s{2,2r} |
s{q,2r} | |
| Omnisnub Alternated omnitruncation |
os{p,q,r} | ht0,1,2,3{p,q,r} | sr{p,q} |
{p}×{ } |
{ }×{r} |
sr{q,r} | |
Five and higher dimensions edit
In five and higher dimensions, there are 3 regular polytopes, the hypercube, simplex and cross-polytope. They are generalisations of the three-dimensional cube, tetrahedron and octahedron, respectively. There are no regular star polytopes in these dimensions. Most uniform higher-dimensional polytopes are obtained by modifying the regular polytopes, or by taking the Cartesian product of polytopes of lower dimensions.
In six, seven and eight dimensions, the exceptional simple Lie groups, E6, E7 and E8 come into play. By placing rings on a nonzero number of nodes of the Coxeter diagrams, one can obtain 39 new 6-polytopes, 127 new 7-polytopes and 255 new 8-polytopes. A notable example is the 421 polytope.
Uniform honeycombs edit
Related to the subject of finite uniform polytopes are uniform honeycombs in Euclidean and hyperbolic spaces. Euclidean uniform honeycombs are generated by affine Coxeter groups and hyperbolic honeycombs are generated by the hyperbolic Coxeter groups. Two affine Coxeter groups can be multiplied together.
There are two classes of hyperbolic Coxeter groups, compact and paracompact. Uniform honeycombs generated by compact groups have finite facets and vertex figures, and exist in 2 through 4 dimensions. Paracompact groups have affine or hyperbolic subgraphs, and infinite facets or vertex figures, and exist in 2 through 10 dimensions.
See also edit
References edit
- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins and J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50. (Extended Schläfli notation used)
- Marco Möller, Vierdimensionale Archimedische Polytope, Dissertation, Universität Hamburg, Hamburg (2004) (in German)
External links edit
- Olshevsky, George. "Uniform polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- uniform, convex polytopes in four dimensions:, Marco Möller (in German)