This article includes a list of general references, but it lacks sufficient corresponding inline citations. (October 2011) |
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular (if also face- and edge-transitive), quasi-regular (if also edge-transitive but not face-transitive), or semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.
There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 quasiregular and 11 semiregular— the non-convex star polyhedra as in 4 Kepler–Poinsot polyhedra and 53 uniform star polyhedra—14 quasiregular and 39 semiregular. There are also many degenerate uniform polyhedra with pairs of edges that coincide, including one found by John Skilling called the great disnub dirhombidodecahedron, Skilling's figure.[1]
Dual polyhedra to uniform polyhedra are face-transitive (isohedral) and have regular vertex figures, and are generally classified in parallel with their dual (uniform) polyhedron. The dual of a regular polyhedron is regular, while the dual of an Archimedean solid is a Catalan solid.
The concept of uniform polyhedron is a special case of the concept of uniform polytope, which also applies to shapes in higher-dimensional (or lower-dimensional) space.
Definition
editThe Original Sin in the theory of polyhedra goes back to Euclid, and through Kepler, Poinsot, Cauchy and many others continues to afflict all the work on this topic (including that of the present author). It arises from the fact that the traditional usage of the term "regular polyhedra" was, and is, contrary to syntax and to logic: the words seem to imply that we are dealing, among the objects we call "polyhedra", with those special ones that deserve to be called "regular". But at each stage— Euclid, Kepler, Poinsot, Hess, Brückner, ... —the writers failed to define what are the "polyhedra" among which they are finding the "regular" ones.
(Branko Grünbaum 1994)
Coxeter, Longuet-Higgins & Miller (1954) define uniform polyhedra to be vertex-transitive polyhedra with regular faces. They define a polyhedron to be a finite set of polygons such that each side of a polygon is a side of just one other polygon, such that no non-empty proper subset of the polygons has the same property. By a polygon they implicitly mean a polygon in 3-dimensional Euclidean space; these are allowed to be non-convex and intersecting each other.[2]
There are some generalizations of the concept of a uniform polyhedron. If the connectedness assumption is dropped, then we get uniform compounds, which can be split as a union of polyhedra, such as the compound of 5 cubes. If we drop the condition that the realization of the polyhedron is non-degenerate, then we get the so-called degenerate uniform polyhedra. These require a more general definition of polyhedra. Grünbaum (1994) gave a rather complicated definition of a polyhedron, while McMullen & Schulte (2002) gave a simpler and more general definition of a polyhedron: in their terminology, a polyhedron is a 2-dimensional abstract polytope with a non-degenerate 3-dimensional realization. Here an abstract polytope is a poset of its "faces" satisfying various condition, a realization is a function from its vertices to some space, and the realization is called non-degenerate if any two distinct faces of the abstract polytope have distinct realizations. Some of the ways they can be degenerate are as follows:
- Hidden faces. Some polyhedra have faces that are hidden, in the sense that no points of their interior can be seen from the outside. These are usually not counted as uniform polyhedra.
- Degenerate compounds. Some polyhedra have multiple edges and their faces are the faces of two or more polyhedra, though these are not compounds in the previous sense since the polyhedra share edges.
- Double covers. Some non-orientable polyhedra have double covers satisfying the definition of a uniform polyhedron. There double covers have doubled faces, edges and vertices. They are usually not counted as uniform polyhedra.
- Double faces. There are several polyhedra with doubled faces produced by Wythoff's construction. Most authors do not allow doubled faces and remove them as part of the construction.
- Double edges. Skilling's figure has the property that it has double edges (as in the degenerate uniform polyhedra) but its faces cannot be written as a union of two uniform polyhedra.
History
editRegular convex polyhedra
edit- The Platonic solids date back to the classical Greeks and were studied by the Pythagoreans, Plato (c. 424 – 348 BC), Theaetetus (c. 417 BC – 369 BC), Timaeus of Locri (c. 420–380 BC), and Euclid (fl. 300 BC). The Etruscans discovered the regular dodecahedron before 500 BC.[3]
Nonregular uniform convex polyhedra
edit- The cuboctahedron was known by Plato.
- Archimedes (287 BC – 212 BC) discovered all of the 13 Archimedean solids. His original book on the subject was lost, but Pappus of Alexandria (c. 290 – c. 350 AD) mentioned Archimedes listed 13 polyhedra.
- Piero della Francesca (1415 – 1492) rediscovered the five truncations of the Platonic solids—truncated tetrahedron, truncated octahedron, truncated cube, truncated dodecahedron, and truncated icosahedron—and included illustrations and calculations of their metric properties in his book De quinque corporibus regularibus. He also discussed the cuboctahedron in a different book.[4]
- Luca Pacioli plagiarized Francesca's work in De divina proportione in 1509, adding the rhombicuboctahedron, calling it an icosihexahedron for its 26 faces, which was drawn by Leonardo da Vinci.
- Johannes Kepler (1571–1630) was the first to publish the complete list of Archimedean solids, in 1619. He also identified the infinite families of uniform prisms and antiprisms.
Regular star polyhedra
edit- Kepler (1619) discovered two of the regular Kepler–Poinsot polyhedra, the small stellated dodecahedron and great stellated dodecahedron.
- Louis Poinsot (1809) discovered the other two, the great dodecahedron and great icosahedron.
- The set of four was proven complete by Augustin-Louis Cauchy in 1813 and named by Arthur Cayley in 1859.
Other 53 nonregular star polyhedra
edit- Of the remaining 53, Edmund Hess (1878) discovered 2, Albert Badoureau (1881) discovered 36 more, and Pitsch (1881) independently discovered 18, of which 3 had not previously been discovered. Together these gave 41 polyhedra.
- The geometer H.S.M. Coxeter discovered the remaining twelve in collaboration with J. C. P. Miller (1930–1932) but did not publish. M.S. Longuet-Higgins and H.C. Longuet-Higgins independently discovered eleven of these. Lesavre and Mercier rediscovered five of them in 1947.
- Coxeter, Longuet-Higgins & Miller (1954) published the list of uniform polyhedra.
- Sopov (1970) proved their conjecture that the list was complete.
- In 1974, Magnus Wenninger published his book Polyhedron models, which lists all 75 nonprismatic uniform polyhedra, with many previously unpublished names given to them by Norman Johnson.
- Skilling (1975) independently proved the completeness and showed that if the definition of uniform polyhedron is relaxed to allow edges to coincide then there is just one extra possibility (the great disnub dirhombidodecahedron).
- In 1987, Edmond Bonan drew all the uniform polyhedra and their duals in 3D with a Turbo Pascal program called Polyca. Most of them were shown during the International Stereoscopic Union Congress held in 1993, at the Congress Theatre, Eastbourne, England; and again in 2005 at the Kursaal of Besançon, France.[5]
- In 1993, Zvi Har'El (1949–2008)[6] produced a complete kaleidoscopic construction of the uniform polyhedra and duals with a computer program called Kaleido and summarized it in a paper Uniform Solution for Uniform Polyhedra, counting figures 1-80.[7]
- Also in 1993, R. Mäder ported this Kaleido solution to Mathematica with a slightly different indexing system.[8]
- In 2002 Peter W. Messer discovered a minimal set of closed-form expressions for determining the main combinatorial and metrical quantities of any uniform polyhedron (and its dual) given only its Wythoff symbol.[9]
Uniform star polyhedra
edit
The 57 nonprismatic nonconvex forms, with exception of the great dirhombicosidodecahedron, are compiled by Wythoff constructions within Schwarz triangles.
Convex forms by Wythoff construction
edit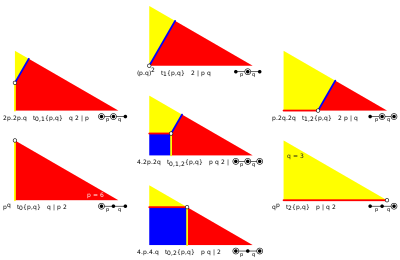

The convex uniform polyhedra can be named by Wythoff construction operations on the regular form.
In more detail the convex uniform polyhedron are given below by their Wythoff construction within each symmetry group.
Within the Wythoff construction, there are repetitions created by lower symmetry forms. The cube is a regular polyhedron, and a square prism. The octahedron is a regular polyhedron, and a triangular antiprism. The octahedron is also a rectified tetrahedron. Many polyhedra are repeated from different construction sources, and are colored differently.
The Wythoff construction applies equally to uniform polyhedra and uniform tilings on the surface of a sphere, so images of both are given. The spherical tilings including the set of hosohedrons and dihedrons which are degenerate polyhedra.
These symmetry groups are formed from the reflectional point groups in three dimensions, each represented by a fundamental triangle (p q r), where p > 1, q > 1, r > 1 and 1/p + 1/q + 1/r < 1.
- Tetrahedral symmetry (3 3 2) – order 24
- Octahedral symmetry (4 3 2) – order 48
- Icosahedral symmetry (5 3 2) – order 120
- Dihedral symmetry (n 2 2), for n = 3,4,5,... – order 4n
The remaining nonreflective forms are constructed by alternation operations applied to the polyhedra with an even number of sides.
Along with the prisms and their dihedral symmetry, the spherical Wythoff construction process adds two regular classes which become degenerate as polyhedra : the dihedra and the hosohedra, the first having only two faces, and the second only two vertices. The truncation of the regular hosohedra creates the prisms.
Below the convex uniform polyhedra are indexed 1–18 for the nonprismatic forms as they are presented in the tables by symmetry form.
For the infinite set of prismatic forms, they are indexed in four families:
- Hosohedra H2... (only as spherical tilings)
- Dihedra D2... (only as spherical tilings)
- Prisms P3... (truncated hosohedra)
- Antiprisms A3... (snub prisms)
Summary tables
edit| Johnson name | Parent | Truncated | Rectified | Bitruncated (tr. dual) |
Birectified (dual) |
Cantellated | Omnitruncated (cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|
| Coxeter diagram | ||||||||
| Extended Schläfli symbol |
||||||||
| {p,q} | t{p,q} | r{p,q} | 2t{p,q} | 2r{p,q} | rr{p,q} | tr{p,q} | sr{p,q} | |
| t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | ht0,1,2{p,q} | |
| Wythoff symbol (p q 2) |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 |
| Vertex figure | pq | q.2p.2p | (p.q)2 | p. 2q.2q | qp | p. 4.q.4 | 4.2p.2q | 3.3.p. 3.q |
| Tetrahedral (3 3 2) |
 3.3.3 |
 3.6.6 |
 3.3.3.3 |
 3.6.6 |
 3.3.3 |
 3.4.3.4 |
 4.6.6 |
 3.3.3.3.3 |
| Octahedral (4 3 2) |
 4.4.4 |
 3.8.8 |
 3.4.3.4 |
 4.6.6 |
 3.3.3.3 |
 3.4.4.4 |
 4.6.8 |
 3.3.3.3.4 |
| Icosahedral (5 3 2) |
 5.5.5 |
 3.10.10 |
 3.5.3.5 |
 5.6.6 |
 3.3.3.3.3 |
 3.4.5.4 |
 4.6.10 |
 3.3.3.3.5 |
And a sampling of dihedral symmetries:
(The sphere is not cut, only the tiling is cut.) (On a sphere, an edge is the arc of the great circle, the shortest way, between its two vertices. Hence, a digon whose vertices are not polar-opposite is flat: it looks like an edge.)
| (p 2 2) | Parent | Truncated | Rectified | Bitruncated (tr. dual) |
Birectified (dual) |
Cantellated | Omnitruncated (cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|
| Coxeter diagram | ||||||||
| Extended Schläfli symbol |
||||||||
| {p,2} | t{p,2} | r{p,2} | 2t{p,2} | 2r{p,2} | rr{p,2} | tr{p,2} | sr{p,2} | |
| t0{p,2} | t0,1{p,2} | t1{p,2} | t1,2{p,2} | t2{p,2} | t0,2{p,2} | t0,1,2{p,2} | ht0,1,2{p,2} | |
| Wythoff symbol | 2 | p 2 | 2 2 | p | 2 | p 2 | 2 p | 2 | p | 2 2 | p 2 | 2 | p 2 2 | | | p 2 2 |
| Vertex figure | p2 | 2.2p.2p | p. 2.p. 2 | p. 4.4 | 2p | p. 4.2.4 | 4.2p.4 | 3.3.3.p |
| Dihedral (2 2 2) |
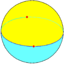 {2,2} |
 2.4.4 |
 2.2.2.2 |
 4.4.2 |
 2.2 |
 2.4.2.4 |
 4.4.4 |
 3.3.3.2 |
| Dihedral (3 2 2) |
 3.3 |
 2.6.6 |
 2.3.2.3 |
 4.4.3 |
 2.2.2 |
 2.4.3.4 |
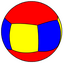 4.4.6 |
 3.3.3.3 |
| Dihedral (4 2 2) |
 4.4 |
2.8.8 |  2.4.2.4 |
 4.4.4 |
 2.2.2.2 |
 2.4.4.4 |
 4.4.8 |
 3.3.3.4 |
| Dihedral (5 2 2) |
 5.5 |
2.10.10 |  2.5.2.5 |
 4.4.5 |
 2.2.2.2.2 |
 2.4.5.4 |
 4.4.10 |
 3.3.3.5 |
| Dihedral (6 2 2) |
 6.6 |
 2.12.12 |
 2.6.2.6 |
 4.4.6 |
 2.2.2.2.2.2 |
 2.4.6.4 |
 4.4.12 |
 3.3.3.6 |
(3 3 2) Td tetrahedral symmetry
editThe tetrahedral symmetry of the sphere generates 5 uniform polyhedra, and a 6th form by a snub operation.
The tetrahedral symmetry is represented by a fundamental triangle with one vertex with two mirrors, and two vertices with three mirrors, represented by the symbol (3 3 2). It can also be represented by the Coxeter group A2 or [3,3], as well as a Coxeter diagram: ![]()
![]()
![]()
![]()
![]() .
.
There are 24 triangles, visible in the faces of the tetrakis hexahedron, and in the alternately colored triangles on a sphere:
| # | Name | Graph A3 |
Graph A2 |
Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [3] (4) |
Pos. 1 [2] (6) |
Pos. 0 [3] (4) |
Faces | Edges | Vertices | ||||||||
| 1 | Tetrahedron | 
|

|

|

|

|
{3,3} |
{3} |
4 | 6 | 4 | ||
| [1] | Birectified tetrahedron (same as tetrahedron) |

|

|

|

|
t2{3,3}={3,3} |
{3} |
4 | 6 | 4 | |||
| 2 | Rectified tetrahedron Tetratetrahedron (same as octahedron) |

|

|

|

|
t1{3,3}=r{3,3} |
{3} |
{3} |
8 | 12 | 6 | ||
| 3 | Truncated tetrahedron | 
|

|

|

|

|
t0,1{3,3}=t{3,3} |
{6} |
{3} |
8 | 18 | 12 | |
| [3] | Bitruncated tetrahedron (same as truncated tetrahedron) |

|

|

|

|
t1,2{3,3}=t{3,3} |
{3} |
{6} |
8 | 18 | 12 | ||
| 4 | Cantellated tetrahedron Rhombitetratetrahedron (same as cuboctahedron) |

|

|

|

|

|
t0,2{3,3}=rr{3,3} |
{3} |
{4} |
{3} |
14 | 24 | 12 |
| 5 | Omnitruncated tetrahedron Truncated tetratetrahedron (same as truncated octahedron) |

|

|

|

|

|
t0,1,2{3,3}=tr{3,3} |
{6} |
{4} |
{6} |
14 | 36 | 24 |
| 6 | Snub tetratetrahedron (same as icosahedron) |
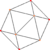
|

|

|

|
sr{3,3} |
{3} |
2 {3} |
{3} |
20 | 30 | 12 | |
(4 3 2) Oh octahedral symmetry
editThe octahedral symmetry of the sphere generates 7 uniform polyhedra, and a 7 more by alternation. Six of these forms are repeated from the tetrahedral symmetry table above.
The octahedral symmetry is represented by a fundamental triangle (4 3 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group B2 or [4,3], as well as a Coxeter diagram: ![]()
![]()
![]()
![]()
![]() .
.
There are 48 triangles, visible in the faces of the disdyakis dodecahedron, and in the alternately colored triangles on a sphere:
| # | Name | Graph B3 |
Graph B2 |
Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [4] (6) |
Pos. 1 [2] (12) |
Pos. 0 [3] (8) |
Faces | Edges | Vertices | ||||||||
| 7 | Cube | 
|

|

|

|
{4,3} |
{4} |
6 | 12 | 8 | |||
| [2] | Octahedron | 
|

|

|

|

|
{3,4} |
{3} |
8 | 12 | 6 | ||
| [4] | Rectified cube Rectified octahedron (Cuboctahedron) |

|

|

|

|
{4,3} |
{4} |
{3} |
14 | 24 | 12 | ||
| 8 | Truncated cube | 
|

|

|

|

|
t0,1{4,3}=t{4,3} |
{8} |
{3} |
14 | 36 | 24 | |
| [5] | Truncated octahedron | 
|

|

|

|
t0,1{3,4}=t{3,4} |
{4} |
{6} |
14 | 36 | 24 | ||
| 9 | Cantellated cube Cantellated octahedron Rhombicuboctahedron |

|

|

|

|

|
t0,2{4,3}=rr{4,3} |
{4} |
{4} |
{3} |
26 | 48 | 24 |
| 10 | Omnitruncated cube Omnitruncated octahedron Truncated cuboctahedron |

|

|

|
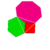
|
t0,1,2{4,3}=tr{4,3} |
{8} |
{4} |
{6} |
26 | 72 | 48 | |
| [6] | Snub octahedron (same as Icosahedron) |

|

|

|

|
= s{3,4}=sr{3,3} |
{3} |
{3} |
20 | 30 | 12 | ||
| [1] | Half cube (same as Tetrahedron) |

|

|

|

|
= h{4,3}={3,3} |
1/2 {3} |
4 | 6 | 4 | |||
| [2] | Cantic cube (same as Truncated tetrahedron) |

|

|

|

|
= h2{4,3}=t{3,3} |
1/2 {6} |
1/2 {3} |
8 | 18 | 12 | ||
| [4] | (same as Cuboctahedron) | 
|

|

|

|

|
= rr{3,3} |
14 | 24 | 12 | |||
| [5] | (same as Truncated octahedron) | 
|

|

|

|

|
= tr{3,3} |
14 | 36 | 24 | |||
| [9] | Cantic snub octahedron (same as Rhombicuboctahedron) |

|

|

|

|

|
s2{3,4}=rr{3,4} |
26 | 48 | 24 | |||
| 11 | Snub cuboctahedron | 
|

|

|
sr{4,3} |
{4} |
2 {3} |
{3} |
38 | 60 | 24 | ||
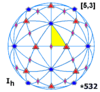
(5 3 2) Ih icosahedral symmetry
editThe icosahedral symmetry of the sphere generates 7 uniform polyhedra, and a 1 more by alternation. Only one is repeated from the tetrahedral and octahedral symmetry table above.
The icosahedral symmetry is represented by a fundamental triangle (5 3 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group G2 or [5,3], as well as a Coxeter diagram: ![]()
![]()
![]()
![]()
![]() .
.
There are 120 triangles, visible in the faces of the disdyakis triacontahedron, and in the alternately colored triangles on a sphere:


| # | Name | Graph (A2) [6] |
Graph (H3) [10] |
Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [5] (12) |
Pos. 1 [2] (30) |
Pos. 0 [3] (20) |
Faces | Edges | Vertices | ||||||||
| 12 | Dodecahedron | 
|

|

|

|
{5,3} |
{5} |
12 | 30 | 20 | |||
| [6] | Icosahedron | 
|

|

|

|

|
{3,5} |
{3} |
20 | 30 | 12 | ||
| 13 | Rectified dodecahedron Rectified icosahedron Icosidodecahedron |

|

|

|
t1{5,3}=r{5,3} |
{5} |
{3} |
32 | 60 | 30 | |||
| 14 | Truncated dodecahedron | 
|
|

|
t0,1{5,3}=t{5,3} |
{10} |
{3} |
32 | 90 | 60 | |||
| 15 | Truncated icosahedron | 
|

|

|

|

|
t0,1{3,5}=t{3,5} |
{5} |
{6} |
32 | 90 | 60 | |
| 16 | Cantellated dodecahedron Cantellated icosahedron Rhombicosidodecahedron |

|

|

|

|
t0,2{5,3}=rr{5,3} |
{5} |
{4} |
{3} |
62 | 120 | 60 | |
| 17 | Omnitruncated dodecahedron Omnitruncated icosahedron Truncated icosidodecahedron |

|

|

|

|

|
t0,1,2{5,3}=tr{5,3} |
{10} |
{4} |
{6} |
62 | 180 | 120 |
| 18 | Snub icosidodecahedron | 
|

|

|
sr{5,3} |
{5} |
2 {3} |
{3} |
92 | 150 | 60 | ||
(p 2 2) Prismatic [p,2], I2(p) family (Dph dihedral symmetry)
editThe dihedral symmetry of the sphere generates two infinite sets of uniform polyhedra, prisms and antiprisms, and two more infinite set of degenerate polyhedra, the hosohedra and dihedra which exist as tilings on the sphere.
The dihedral symmetry is represented by a fundamental triangle (p 2 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group I2(p) or [n,2], as well as a prismatic Coxeter diagram: ![]()
![]()
![]()
![]()
![]() .
.
Below are the first five dihedral symmetries: D2 ... D6. The dihedral symmetry Dp has order 4n, represented the faces of a bipyramid, and on the sphere as an equator line on the longitude, and n equally-spaced lines of longitude.
(2 2 2) Dihedral symmetry
editThere are 8 fundamental triangles, visible in the faces of the square bipyramid (Octahedron) and alternately colored triangles on a sphere:
| # | Name | Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [2] (2) |
Pos. 1 [2] (2) |
Pos. 0 [2] (2) |
Faces | Edges | Vertices | ||||||
| D2 H2 |
Digonal dihedron, digonal hosohedron |
|
{2,2} |
{2} |
2 | 2 | 2 | ||||
| D4 | Truncated digonal dihedron (same as square dihedron) |

|
t{2,2}={4,2} |
{4} |
2 | 4 | 4 | ||||
| P4 [7] |
Omnitruncated digonal dihedron (same as cube) |

|

|

|
t0,1,2{2,2}=tr{2,2} |
{4} |
{4} |
{4} |
6 | 12 | 8 |
| A2 [1] |
Snub digonal dihedron (same as tetrahedron) |

|

|

|
sr{2,2} |
2 {3} |
4 | 6 | 4 | ||
(3 2 2) D3h dihedral symmetry
editThere are 12 fundamental triangles, visible in the faces of the hexagonal bipyramid and alternately colored triangles on a sphere:
| # | Name | Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [3] (2) |
Pos. 1 [2] (3) |
Pos. 0 [2] (3) |
Faces | Edges | Vertices | ||||||
| D3 | Trigonal dihedron | 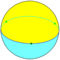
|
{3,2} |
{3} |
2 | 3 | 3 | ||||
| H3 | Trigonal hosohedron | 
|
{2,3} |
{2} |
3 | 3 | 2 | ||||
| D6 | Truncated trigonal dihedron (same as hexagonal dihedron) |

|
t{3,2} |
{6} |
2 | 6 | 6 | ||||
| P3 | Truncated trigonal hosohedron (Triangular prism) |

|

|

|
t{2,3} |
{3} |
{4} |
5 | 9 | 6 | |
| P6 | Omnitruncated trigonal dihedron (Hexagonal prism) |

|

|

|
t0,1,2{2,3}=tr{2,3} |
{6} |
{4} |
{4} |
8 | 18 | 12 |
| A3 [2] |
Snub trigonal dihedron (same as Triangular antiprism) (same as octahedron) |

|

|

|
sr{2,3} |
{3} |
2 {3} |
8 | 12 | 6 | |
| P3 | Cantic snub trigonal dihedron (Triangular prism) |

|

|

|
s2{2,3}=t{2,3} |
5 | 9 | 6 | |||
(4 2 2) D4h dihedral symmetry
editThere are 16 fundamental triangles, visible in the faces of the octagonal bipyramid and alternately colored triangles on a sphere:
| # | Name | Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [4] (2) |
Pos. 1 [2] (4) |
Pos. 0 [2] (4) |
Faces | Edges | Vertices | ||||||
| D4 | square dihedron | 
|
{4,2} |
{4} |
2 | 4 | 4 | ||||
| H4 | square hosohedron | 
|
{2,4} |
{2} |
4 | 4 | 2 | ||||
| D8 | Truncated square dihedron (same as octagonal dihedron) |
t{4,2} |
{8} |
2 | 8 | 8 | |||||
| P4 [7] |
Truncated square hosohedron (Cube) |

|

|

|
t{2,4} |
{4} |
{4} |
6 | 12 | 8 | |
| D8 | Omnitruncated square dihedron (Octagonal prism) |

|

|
t0,1,2{2,4}=tr{2,4} |
{8} |
{4} |
{4} |
10 | 24 | 16 | |
| A4 | Snub square dihedron (Square antiprism) |

|

|

|
sr{2,4} |
{4} |
2 {3} |
10 | 16 | 8 | |
| P4 [7] |
Cantic snub square dihedron (Cube) |

|

|

|
s2{4,2}=t{2,4} |
6 | 12 | 8 | |||
| A2 [1] |
Snub square hosohedron (Digonal antiprism) (Tetrahedron) |

|

|

|
s{2,4}=sr{2,2} |
4 | 6 | 4 | |||
(5 2 2) D5h dihedral symmetry
editThere are 20 fundamental triangles, visible in the faces of the decagonal bipyramid and alternately colored triangles on a sphere:
| # | Name | Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [5] (2) |
Pos. 1 [2] (5) |
Pos. 0 [2] (5) |
Faces | Edges | Vertices | ||||||
| D5 | Pentagonal dihedron | 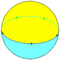
|
{5,2} |
{5} |
2 | 5 | 5 | ||||
| H5 | Pentagonal hosohedron | 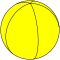
|
{2,5} |
{2} |
5 | 5 | 2 | ||||
| D10 | Truncated pentagonal dihedron (same as decagonal dihedron) |
t{5,2} |
{10} |
2 | 10 | 10 | |||||
| P5 | Truncated pentagonal hosohedron (same as pentagonal prism) |

|

|

|
t{2,5} |
{5} |
{4} |
7 | 15 | 10 | |
| P10 | Omnitruncated pentagonal dihedron (Decagonal prism) |
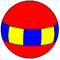
|

|
t0,1,2{2,5}=tr{2,5} |
{10} |
{4} |
{4} |
12 | 30 | 20 | |
| A5 | Snub pentagonal dihedron (Pentagonal antiprism) |

|

|

|
sr{2,5} |
{5} |
2 {3} |
12 | 20 | 10 | |
| P5 | Cantic snub pentagonal dihedron (Pentagonal prism) |

|

|

|
s2{5,2}=t{2,5} |
7 | 15 | 10 | |||
(6 2 2) D6h dihedral symmetry
editThere are 24 fundamental triangles, visible in the faces of the dodecagonal bipyramid and alternately colored triangles on a sphere.
| # | Name | Picture | Tiling | Vertex figure |
Coxeter and Schläfli symbols |
Face counts by position | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pos. 2 [6] (2) |
Pos. 1 [2] (6) |
Pos. 0 [2] (6) |
Faces | Edges | Vertices | ||||||
| D6 | Hexagonal dihedron | 
|
{6,2} |
{6} |
2 | 6 | 6 | ||||
| H6 | Hexagonal hosohedron | 
|
{2,6} |
{2} |
6 | 6 | 2 | ||||
| D12 | Truncated hexagonal dihedron (same as dodecagonal dihedron) |

|
t{6,2} |
{12} |
2 | 12 | 12 | ||||
| H6 | Truncated hexagonal hosohedron (same as hexagonal prism) |

|

|

|
t{2,6} |
{6} |
{4} |
8 | 18 | 12 | |
| P12 | Omnitruncated hexagonal dihedron (Dodecagonal prism) |

|

|

|
t0,1,2{2,6}=tr{2,6} |
{12} |
{4} |
{4} |
14 | 36 | 24 |
| A6 | Snub hexagonal dihedron (Hexagonal antiprism) |

|

|

|
sr{2,6} |
{6} |
2 {3} |
14 | 24 | 12 | |
| P3 | Cantic hexagonal dihedron (Triangular prism) |

|

|

|
h2{6,2}=t{2,3} |
5 | 9 | 6 | |||
| P6 | Cantic snub hexagonal dihedron (Hexagonal prism) |

|

|

|
s2{6,2}=t{2,6} |
8 | 18 | 12 | |||
| A3 [2] |
Snub hexagonal hosohedron (same as Triangular antiprism) (same as octahedron) |

|

|

|
s{2,6}=sr{2,3} |
8 | 12 | 6 | |||
Wythoff construction operators
edit| Operation | Symbol | Coxeter diagram |
Description |
|---|---|---|---|
| Parent | {p,q} t0{p,q} |
Any regular polyhedron or tiling | |
| Rectified (r) | r{p,q} t1{p,q} |
The edges are fully truncated into single points. The polyhedron now has the combined faces of the parent and dual. Polyhedra are named by the number of sides of the two regular forms: {p,q} and {q,p}, like cuboctahedron for r{4,3} between a cube and octahedron. | |
| Birectified (2r) (also dual) |
2r{p,q} t2{p,q} |
 | |
| Truncated (t) | t{p,q} t0,1{p,q} |
Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated polyhedron. The polyhedron has its original faces doubled in sides, and contains the faces of the dual.
| |
| Bitruncated (2t) (also truncated dual) |
2t{p,q} t1,2{p,q} |
A bitruncation can be seen as the truncation of the dual. A bitruncated cube is a truncated octahedron. | |
| Cantellated (rr) (Also expanded) |
rr{p,q} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place. A uniform cantellation is halfway between both the parent and dual forms. A cantellated polyhedron is named as a rhombi-r{p,q}, like rhombicuboctahedron for rr{4,3}.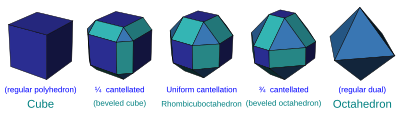
| |
| Cantitruncated (tr) (Also omnitruncated) |
tr{p,q} t0,1,2{p,q} |
The truncation and cantellation operations are applied together to create an omnitruncated form which has the parent's faces doubled in sides, the dual's faces doubled in sides, and squares where the original edges existed. |
| Operation | Symbol | Coxeter diagram |
Description |
|---|---|---|---|
| Snub rectified (sr) | sr{p,q} | The alternated cantitruncated. All the original faces end up with half as many sides, and the squares degenerate into edges. Since the omnitruncated forms have 3 faces/vertex, new triangles are formed. Usually these alternated faceting forms are slightly deformed thereafter in order to end again as uniform polyhedra. The possibility of the latter variation depends on the degree of freedom.
| |
| Snub (s) | s{p,2q} | Alternated truncation | |
| Cantic snub (s2) | s2{p,2q} | ||
| Alternated cantellation (hrr) | hrr{2p,2q} | Only possible in uniform tilings (infinite polyhedra), alternation of For example, | |
| Half (h) | h{2p,q} | Alternation of | |
| Cantic (h2) | h2{2p,q} | Same as | |
| Half rectified (hr) | hr{2p,2q} | Only possible in uniform tilings (infinite polyhedra), alternation of For example, | |
| Quarter (q) | q{2p,2q} | Only possible in uniform tilings (infinite polyhedra), same as For example, |
See also
edit- Polyhedron
- List of uniform polyhedra
- List of Johnson solids
- List of Wenninger polyhedron models
- Polyhedron model
- Uniform tiling
- Uniform tilings in hyperbolic plane
- Pseudo-uniform polyhedron
- List of shapes
Notes
edit- ^ Diudea (2018), p. https://books.google.com/books?id=p_06DwAAQBAJ&pg=PA40 40].
- ^ Coxeter, Longuet-Higgins & Miller (1954).
- ^ Regular Polytopes, p.13
- ^ Piero della Francesca's Polyhedra
- ^ Edmond Bonan, "Polyèdres Eastbourne 1993", Stéréo-Club Français 1993
- ^ Dr. Zvi Har’El (December 14, 1949 – February 2, 2008) and International Jules Verne Studies - A Tribute
- ^ Har'el, Zvi (1993). "Uniform Solution for Uniform Polyhedra" (PDF). Geometriae Dedicata. 47: 57–110. doi:10.1007/BF01263494. Zvi Har’El, Kaleido software, Images, dual images
- ^ Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [1]
- ^ Messer, Peter W. (2002). "Closed-Form Expressions for Uniform Polyhedra and Their Duals". Discrete & Computational Geometry. 27 (3): 353–375. doi:10.1007/s00454-001-0078-2.
References
edit- Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [2]
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra" (PDF). Philosophical Transactions of the Royal Society A. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.
- Diudea, M. V. (2018), Multi-shell Polyhedral Clusters, Springer, doi:10.1007/978-3-319-64123-2, ISBN 978-3-319-64123-2
- Grünbaum, B. (1994), "Polyhedra with Hollow Faces", in Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. (eds.), Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational, Springer, pp. 43–70, doi:10.1007/978-94-011-0924-6_3, ISBN 978-94-010-4398-4
- McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Cambridge University Press
- Skilling, J. (1975). "The complete set of uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 278 (1278): 111–135. Bibcode:1975RSPTA.278..111S. doi:10.1098/rsta.1975.0022. ISSN 0080-4614. JSTOR 74475. MR 0365333. S2CID 122634260.
- Sopov, S. P. (1970). "A proof of the completeness on the list of elementary homogeneous polyhedra". Ukrainskiui Geometricheskiui Sbornik (8): 139–156. MR 0326550.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 978-0-521-09859-5.
External links
edit- Weisstein, Eric W. "Uniform Polyhedron". MathWorld.
- Uniform Solution for Uniform Polyhedra
- The Uniform Polyhedra
- Virtual Polyhedra Uniform Polyhedra
- Uniform polyhedron gallery
- Uniform Polyhedron -- from Wolfram MathWorld Has a visual chart of all 75