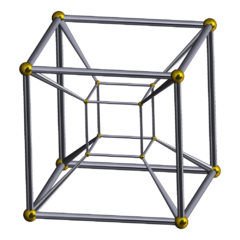
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube.[1] Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.
| Tesseract 8-cell (4-cube) | |
|---|---|
 | |
| Type | Convex regular 4-polytope |
| Schläfli symbol | {4,3,3} t0,3{4,3,2} or {4,3}×{ } t0,2{4,2,4} or {4}×{4} t0,2,3{4,2,2} or {4}×{ }×{ } t0,1,2,3{2,2,2} or { }×{ }×{ }×{ } |
| Coxeter diagram | |
| Cells | 8 {4,3} |
| Faces | 24 {4} |
| Edges | 32 |
| Vertices | 16 |
| Vertex figure |  Tetrahedron |
| Petrie polygon | octagon |
| Coxeter group | B4, [3,3,4] |
| Dual | 16-cell |
| Properties | convex, isogonal, isotoxal, isohedral, Hanner polytope |
| Uniform index | 10 |


The tesseract is also called an 8-cell, C8, (regular) octachoron, or cubic prism. It is the four-dimensional measure polytope, taken as a unit for hypervolume.[2] Coxeter labels it the γ4 polytope.[3] The term hypercube without a dimension reference is frequently treated as a synonym for this specific polytope.
The Oxford English Dictionary traces the word tesseract to Charles Howard Hinton's 1888 book A New Era of Thought. The term derives from the Greek téssara (τέσσαρα 'four') and aktís (ἀκτίς 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled the word as tessaract.[4]
Geometry edit
As a regular polytope with three cubes folded together around every edge, it has Schläfli symbol {4,3,3} with hyperoctahedral symmetry of order 384. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }, with symmetry order 96. As a 4-4 duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}×{4}, with symmetry order 64. As an orthotope it can be represented by composite Schläfli symbol { } × { } × { } × { } or { }4, with symmetry order 16.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. The dual polytope of the tesseract is the 16-cell with Schläfli symbol {3,3,4}, with which it can be combined to form the compound of tesseract and 16-cell.
Each edge of a regular tesseract is of the same length. This is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
A tesseract is bounded by eight three-dimensional hyperplanes. Each pair of non-parallel hyperplanes intersects to form 24 square faces. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, a tesseract consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Coordinates edit
A unit tesseract has side length 1, and is typically taken as the basic unit for hypervolume in 4-dimensional space. The unit tesseract in a Cartesian coordinate system for 4-dimensional space has two opposite vertices at coordinates [0, 0, 0, 0] and [1, 1, 1, 1], and other vertices with coordinates at all possible combinations of 0s and 1s. It is the Cartesian product of the closed unit interval [0, 1] in each axis.
Sometimes a unit tesseract is centered at the origin, so that its coordinates are the more symmetrical This is the Cartesian product of the closed interval in each axis.
Another commonly convenient tesseract is the Cartesian product of the closed interval [−1, 1] in each axis, with vertices at coordinates (±1, ±1, ±1, ±1). This tesseract has side length 2 and hypervolume 24 = 16.
Net edit
An unfolding of a polytope is called a net. There are 261 distinct nets of the tesseract.[5] The unfoldings of the tesseract can be counted by mapping the nets to paired trees (a tree together with a perfect matching in its complement).
Construction edit
The construction of hypercubes can be imagined the following way:
- 1-dimensional: Two points A and B can be connected to become a line, giving a new line segment AB.
- 2-dimensional: Two parallel line segments AB and CD separated by a distance of AB can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH separated by a distance of AB can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP separated by a distance of AB can be connected to become a tesseract, with the corners marked as ABCDEFGHIJKLMNOP. However, this parallel positioning of two cubes such that their 8 corresponding pairs of vertices are each separated by a distance of AB can only be achieved in a space of 4 or more dimensions.
The 8 cells of the tesseract may be regarded (three different ways) as two interlocked rings of four cubes.[6]
The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts (16-cells). It can also be triangulated into 4-dimensional simplices (irregular 5-cells) that share their vertices with the tesseract. It is known that there are 92487256 such triangulations[7] and that the fewest 4-dimensional simplices in any of them is 16.[8]
The dissection of the tesseract into instances of its characteristic simplex (a particular orthoscheme with Coxeter diagram ) is the most basic direct construction of the tesseract possible. The characteristic 5-cell of the 4-cube is a fundamental region of the tesseract's defining symmetry group, the group which generates the B4 polytopes. The tesseract's characteristic simplex directly generates the tesseract through the actions of the group, by reflecting itself in its own bounding facets (its mirror walls).
Radial equilateral symmetry edit
The radius of a hypersphere circumscribed about a regular polytope is the distance from the polytope's center to one of the vertices, and for the tesseract this radius is equal to its edge length; the diameter of the sphere, the length of the diagonal between opposite vertices of the tesseract, is twice the edge length. Only a few uniform polytopes have this property, including the four-dimensional tesseract and 24-cell, the three-dimensional cuboctahedron, and the two-dimensional hexagon. In particular, the tesseract is the only hypercube (other than a zero-dimensional point) that is radially equilateral. The longest vertex-to-vertex diagonal of an -dimensional hypercube of unit edge length is which for the square is for the cube is and only for the tesseract is edge lengths.
An axis-aligned tesseract inscribed in a unit-radius 3-sphere has vertices with coordinates
Properties edit
For a tesseract with side length s:
- Hypervolume (4D):
- Surface "volume" (3D):
- Face diagonal:
- Cell diagonal:
- 4-space diagonal:
As a configuration edit
This configuration matrix represents the tesseract. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole tesseract. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[9] For example, the 2 in the first column of the second row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 4 in the second column of the first row indicates that 4 edges meet at each vertex.
Projections edit
It is possible to project tesseracts into three- and two-dimensional spaces, similarly to projecting a cube into two-dimensional space.
The cell-first parallel projection of the tesseract into three-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining six cells are projected onto the six square faces of the cube.
The face-first parallel projection of the tesseract into three-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the four remaining cells project to the side faces.
The edge-first parallel projection of the tesseract into three-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto six rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The vertex-first parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedral envelope. Two vertices of the tesseract are projected to the origin. There are exactly two ways of dissecting a rhombic dodecahedron into four congruent rhombohedra, giving a total of eight possible rhombohedra, each a projected cube of the tesseract. This projection is also the one with maximal volume. One set of projection vectors are u = (1,1,−1,−1), v = (−1,1,−1,1), w = (1,−1,−1,1).
| Coxeter plane | B4 | B4 --> A3 | A3 |
|---|---|---|---|
| Graph | |||
| Dihedral symmetry | [8] | [4] | [4] |
| Coxeter plane | Other | B3 / D4 / A2 | B2 / D3 |
| Graph | |||
| Dihedral symmetry | [2] | [6] | [4] |
| A 3D projection of a tesseract performing a simple rotation about a plane in 4-dimensional space. The plane bisects the figure from front-left to back-right and top to bottom. |
A 3D projection of a tesseract performing a double rotation about two orthogonal planes in 4-dimensional space. |
| Perspective with hidden volume elimination. The red corner is the nearest in 4D and has 4 cubical cells meeting around it. |
The tetrahedron forms the convex hull of the tesseract's vertex-centered central projection. Four of 8 cubic cells are shown. The 16th vertex is projected to infinity and the four edges to it are not shown. |
Stereographic projection (Edges are projected onto the 3-sphere) |
| Stereoscopic 3D projection of a tesseract (parallel view) |
| Stereoscopic 3D Disarmed Hypercube |
Tessellation edit
The tesseract, like all hypercubes, tessellates Euclidean space. The self-dual tesseractic honeycomb consisting of 4 tesseracts around each face has Schläfli symbol {4,3,3,4}. Hence, the tesseract has a dihedral angle of 90°.[10]
The tesseract's radial equilateral symmetry makes its tessellation the unique regular body-centered cubic lattice of equal-sized spheres, in any number of dimensions.
Related polytopes and honeycombs edit
The tesseract is 4th in a series of hypercube:
| Line segment | Square | Cube | 4-cube | 5-cube | 6-cube | 7-cube | 8-cube |
The tesseract (8-cell) is the third in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).
| Regular convex 4-polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | |||
| Name | 5-cell Hyper-tetrahedron |
16-cell Hyper-octahedron |
8-cell Hyper-cube |
24-cell
|
600-cell Hyper-icosahedron |
120-cell Hyper-dodecahedron | |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Coxeter mirrors | |||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | |
| Graph | |||||||
| Vertices | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral | |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular | |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons | |
| Cells | 5 tetrahedra | 16 tetrahedra | 8 cubes | 24 octahedra | 600 tetrahedra | 120 dodecahedra | |
| Tori | 1 5-tetrahedron | 2 8-tetrahedron | 2 4-cube | 4 6-octahedron | 20 30-tetrahedron | 12 10-dodecahedron | |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells | |
| Great polygons | 2 squares x 3 | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | ||
| Petrie polygons | 1 pentagon x 2 | 1 octagon x 3 | 2 octagons x 4 | 2 dodecagons x 4 | 4 30-gons x 6 | 20 30-gons x 4 | |
| Long radius | |||||||
| Edge length | |||||||
| Short radius | |||||||
| Area | |||||||
| Volume | |||||||
| 4-Content | |||||||
As a uniform duoprism, the tesseract exists in a sequence of uniform duoprisms: {p}×{4}.
The regular tesseract, along with the 16-cell, exists in a set of 15 uniform 4-polytopes with the same symmetry. The tesseract {4,3,3} exists in a sequence of regular 4-polytopes and honeycombs, {p,3,3} with tetrahedral vertex figures, {3,3}. The tesseract is also in a sequence of regular 4-polytope and honeycombs, {4,3,p} with cubic cells.
| Orthogonal | Perspective |
|---|---|
| 4{4}2, with 16 vertices and 8 4-edges, with the 8 4-edges shown here as 4 red and 4 blue squares | |
The regular complex polytope 4{4}2, , in has a real representation as a tesseract or 4-4 duoprism in 4-dimensional space. 4{4}2 has 16 vertices, and 8 4-edges. Its symmetry is 4[4]2, order 32. It also has a lower symmetry construction, , or 4{}×4{}, with symmetry 4[2]4, order 16. This is the symmetry if the red and blue 4-edges are considered distinct.[11]
In popular culture edit
Since their discovery, four-dimensional hypercubes have been a popular theme in art, architecture, and science fiction. Notable examples include:
- "And He Built a Crooked House", Robert Heinlein's 1940 science fiction story featuring a building in the form of a four-dimensional hypercube.[12] This and Martin Gardner's "The No-Sided Professor", published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle, and the hypercube (tesseract).
- Crucifixion (Corpus Hypercubus), a 1954 oil painting by Salvador Dalí featuring a four-dimensional hypercube unfolded into a three-dimensional Latin cross.[13]
- The Grande Arche, a monument and building near Paris, France, completed in 1989. According to the monument's engineer, Erik Reitzel, the Grande Arche was designed to resemble the projection of a hypercube.[14]
- Fez, a video game where one plays a character who can see beyond the two dimensions other characters can see, and must use this ability to solve platforming puzzles. Features "Dot", a tesseract who helps the player navigate the world and tells how to use abilities, fitting the theme of seeing beyond human perception of known dimensional space.[15]
The word tesseract was later adopted for numerous other uses in popular culture, including as a plot device in works of science fiction, often with little or no connection to the four-dimensional hypercube; see Tesseract (disambiguation).
See also edit
Notes edit
- ^ "The Tesseract - a 4-dimensional cube". www.cut-the-knot.org. Retrieved 2020-11-09.
- ^ Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- ^ Coxeter 1973, pp. 122–123, §7.2. illustration Fig 7.2C.
- ^ "tesseract". Oxford English Dictionary (Online ed.). Oxford University Press. 199669. (Subscription or participating institution membership required.)
- ^ "Unfolding an 8-cell". Unfolding.apperceptual.com. Retrieved 21 January 2018.
- ^ Coxeter 1970, p. 18.
- ^ Pournin, Lionel (2013), "The flip-Graph of the 4-dimensional cube is connected", Discrete & Computational Geometry, 49 (3): 511–530, arXiv:1201.6543, doi:10.1007/s00454-013-9488-y, MR 3038527, S2CID 30946324
- ^ Cottle, Richard W. (1982), "Minimal triangulation of the 4-cube", Discrete Mathematics, 40: 25–29, doi:10.1016/0012-365X(82)90185-6, MR 0676709
- ^ Coxeter 1973, p. 12, §1.8 Configurations.
- ^ Coxeter 1973, p. 293.
- ^ Coxeter, H. S. M., Regular Complex Polytopes, second edition, Cambridge University Press, (1991).
- ^ Fowler, David (2010), "Mathematics in Science Fiction: Mathematics as Science Fiction", World Literature Today, 84 (3): 48–52, doi:10.1353/wlt.2010.0188, JSTOR 27871086, S2CID 115769478
- ^ Kemp, Martin (1 January 1998), "Dali's dimensions", Nature, 391 (27): 27, Bibcode:1998Natur.391...27K, doi:10.1038/34063, S2CID 5317132
- ^ Ursyn, Anna (2016), "Knowledge Visualization and Visual Literacy in Science Education", Knowledge Visualization and Visual Literacy in Science Education, Information Science Reference, p. 91, ISBN 9781522504818
- ^ "Dot (Character) - Giant Bomb". Giant Bomb. Retrieved 21 January 2018.
References edit
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123.
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Kaleidoscopes: Selected Writings of H.S.M. Coxeter, Wiley-Interscience Publication ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M. (1970), "Twisted Honeycombs", Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, 4, Providence, Rhode Island: American Mathematical Society
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- T. Gosset (1900) On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan.
- T. Proctor Hall (1893) "The projection of fourfold figures on a three-flat", American Journal of Mathematics 15:179–89.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
External links edit
- Klitzing, Richard. "4D uniform polytopes (polychora) x4o3o3o - tes".
- ken perlin's home page A way to visualize hypercubes, by Ken Perlin
- Some Notes on the Fourth Dimension includes animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- Tesseract animation with hidden volume elimination