User:UpdateNerd/Golden ratio

This page is about the number. For the pop music album, see The Golden Ratio (album). For the related sequence of numbers, see Fibonacci number.

Line segments in the golden ratio

A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship ${\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi$.

The golden spiral is approximated by tiling the square of Fibonacci numbers, which are related by the golden ratio.

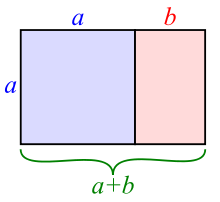
In mathematics, two quantities are said to be in the golden ratio if their proportion is congruent to that of their sum to the larger of the two quantities. For quantities a and b, where a > b > 0, this can be expressed:

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

The golden ratio is also called the golden proportion, golden mean and golden section; older names include the divine proportion, divine section (Latin: sectio divina), golden cut, and golden number. It is an irrational number represented by the Greek letter Phi (φ), and with the value:

${\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$

The golden ratio manifests in nature, including the spiral arrangement of leaves and other plant parts. Most scholars consider it unlikely that the ancient world before Pythagoras knew of the ratio or understood its mathematical and geometrical properties, such as its self-similarity and presence in the dimensions of a regular pentagon, dodecahedron, and icosahedron. Euclid provides the first known definition of the "extreme and mean ratio" in his Elements (c. 300 BC).

The golden ratio was also studied prominently by Renaissance polymaths such as Luca Pacioli and Johannes Kepler, who studied its role in geometry and nature. Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to the golden ratio—especially in the form of the golden rectangle. The ratio has also been used to make many dubious claims which have been discredited by scholars.

Calculation

List of numbers Irrational numbers ζ(3) √2 √3 √5 φ e π
Binary	1.1001111000110111011...
Decimal	1.6180339887498948482...
Hexadecimal	1.9E3779B97F4A7C15F39...
Continued fraction	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
Algebraic form	${\frac {1+{\sqrt {5}}}{2}}$
Infinite series	${\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}$

Two quantities a and b are said to be in the golden ratio φ if:

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

One method for finding the value of φ is to start with the left fraction. Through simplifying the fraction and substituting in b/a = 1/φ,

${\frac {a+b}{a}}={\frac {a}{a}}+{\frac {b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}.$

Therefore,

$1+{\frac {1}{\varphi }}=\varphi .$

Multiplying by φ gives

$\varphi +1=\varphi ^{2}$

which can be rearranged to

${\varphi }^{2}-\varphi -1=0.$

Using the quadratic formula, two solutions are obtained:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$

and

$\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.6180\,339887\dots$

Because φ is the ratio between positive quantities φ is necessarily positive:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$

History

See also: Fibonacci number § History

A pentagram with colored line segments of different lengths, related to one another via the golden ratio.

Though ancient Greek philosopher Pythagoras (c. 570 BC–c. 495 BC) left behind no writing, he is generally credited with knowledge of the golden ratio and the related dodecahedron, and imparting this knowledge to his followers; their symbol was the pentagram. According to one story, the 5th-century Pythagorean Hippasus discovered that the golden ratio was an irrational number, surprising other Pythagoreans. Hippasus was also the first to write of the dodecahedron, with Theaetetus (c. 417–c. 369 BC) being the first to describe all five possible regular solids. Euclid's Elements (c. 300 BC) provides several propositions and their proofs employing the golden ratio, using it in the construction of the pentagon, icosahedron and dodecahedron. It also contains the first known definition:

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.

Alexandrians Ptolemy calculated trigonometric chords for angles relating to the golden ratio in the second century, and Pappus made calculations for the comparison of Platonic solids related to the golden ratio c. 340 AD. Abū Kāmil Shujāʿ ibn Aslam (c. 850–930) employed the golden ratio in his calculations of pentagons; some of his work influenced that of Fibonacci. Piero della Francesca (c. 1412–1492) developed geometrical solutions involving pentagons and the Platonic solids; much of his work was translated by Luca Pacioli in his 1509 Divina proportione (Divine proportion), which points out that golden rectangles can be inscribed by an icosahedron. Other 16th-century mathematicians such as Flussates Candalla and Rafael Bombelli solved problems related to pentagons and Platonic solids using the golden ratio.

Kepler's illustration of a regular dodecahedron

German mathematician Simon Jacob (d. 1564) noted that consecutive Fibonacci numbers converge to the golden ratio; this was rediscovered by Johannes Kepler in 1608. In 1597, Kepler's former professor Michael Maestlin wrote him the first known decimal approximation of the (inverse) golden ratio as "about 0.6180340", and Kepler wrote to Maestlin of the Kepler triangle, which combines the golden ratio with the Pythagorean theorem. Kepler's 1619 Harmonices Mundi also featured illustrations of solids and tiling patterns related to the golden ratio.

18th-century mathematicians Abraham de Moivre, Daniel Bernoulli, and Leonhard Euler used a golden ratio-based formula which finds the value of a Fibonacci number based on its placement in the sequence; in 1843 this was rediscovered by Jacques Philippe Marie Binet, for whom it was named. Martin Ohm is believed to have been the first to use the term Goldener Schnitt ('golden section') to describe the ratio in 1835. In 1885, Charles Henry published his Introduction to a scientific aesthetic, which placed importance on the golden ratio.

Phi (pronounced 'fee' or 'fai')

Around 1909, mathematician Mark Barr began using Greek letter Phi (φ) as a symbol for the golden ratio; it has also been represented by tau (τ), the first letter of the ancient Greek τομή—('cut' or 'section'). In 1966, Fibonacci Quarterly published φ calculated to 4,600 digits; thirty years later, it was calculated to 10 million decimal places. In 1974, Roger Penrose discovered a form of tiling derived from the diagonal division of pentagons which is related to the golden ratio both in the relationship of areas of its two rhombic tiles and their relative frequency within the pattern. This led to Dan Shechtman's early 1980s discovery of quasicrystals, which exhibit icosahedral symmetry, particularly within aluminium alloys.

Applications

Architecture

Further information: Mathematics and architecture

It has been speculated that the golden ratio was used by the designers of the Naqsh-e Jahan Square (1629) and the adjacent Lotfollah Mosque. A 2004 geometrical analysis of earlier research into the Great Mosque of Kairouan reveals a consistent application of the golden ratio throughout the design. Proportions close to the golden ratio were found in the overall layout and the dimensions of the prayer space, the court, and the minaret. However, these areas were not part of the original plan, and were likely added in a reconstruction.

The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier's faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as:

rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned.

Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci's Vitruvian Man, the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture. In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body's height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier's 1927 Villa Stein in Garches exemplified the Modulor system's application. The villa's rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.

Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.

Art

Further information: Mathematics and art

A floor mosaic featuring a small stellated dodecahedron by Paolo Uccello c. 1430, St Mark's Basilica

In 1509, Luca Pacioli published the three-volume Divina proportione (Divine proportion). A Franciscan friar and mathematician, Pacioli was also trained and keenly interested in art. Divina proportione explored the mathematics of the golden ratio. Though it is often said that Pacioli advocated the golden ratio's application to yield pleasing, harmonious proportions, Mario Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions. In the book, Pacioli argues for calling the golden ratio the "Divine Proportion", the work's title.

Divina proportione contains illustrations of polyhedra by Leonardo da Vinci; this collaboration has led some to speculate that Leonardo incorporated the golden ratio in his work, but this is not supported by any of his writings. In 2015, a group of scientists used imaging software to find that Michelangelo used the golden ratio in The Creation of Adam on the Sistine Chapel ceiling (c. 1508–1512). The vanishing point in Albrecht Dürer's Melencolia I (1514) divides the diameter of a rainbow in the golden proportion.

Early 20th-century artist Jay Hambidge's concept of "dynamic symmetry" included the golden ratio and logarithmic spiral, which he postulated had more life than the "static symmetry" of equilateral forms. Salvador Dalí, influenced by the works of Matila Ghyka, explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle, and a huge dodecahedron, in perspective so that its edges appear in golden ratio to one another, dominates the composition. Other 20th-century artists such as Gino Severini, Juan Gris, and Jacques Lipchitz used the golden ratio in Cubist or Cubism-related art. Igael Tumarkin also included the formula for ϕ in a painting.

A statistical study performed in 1999 on 565 works of art by different painters found that they did not use the golden ratio in their canvas sizes. The study concluded that the average ratio of the two sides of the paintings studied is 1.34, with averages for individual artists ranging from 1.04 to 1.46. On the other hand, Pablo Tosto listed over 350 works by well-known artists, including more than 100 which have canvasses with golden rectangle and root-5 proportions.

Depiction of the proportions in a medieval manuscript, with "page proportion 2:3. Margin proportions 1:1:2:3. Text area proportioned in the Golden Section."

Books and design

Further information: Canons of page construction

Historian John Man states that the text area of the Gutenberg Bible was based on a 5:8 golden ratio proportion. According to Jan Tschichold,

There was a time when deviations from the truly beautiful page proportions 2:3, 1:√3, and the Golden Section were rare. Many books produced between 1550 and 1770 show these proportions exactly, to within half a millimeter.

The golden ratio is used in everyday design, for example in the proportions of light switch plates, playing cards, postcards, posters, and widescreen televisions. The 16:10 aspect ratio commonly used for computer displays approximates the golden ratio.

Music

See also: Fibonacci number § Music

Two pentagons inscribed by a circle are featured in Stradivari's drawing of a violin

Antonio Stradivari (1644–1737) placed the eyes of the f-holes on violins he made according to the golden ratio; however, most agree that this is simply aesthetic and has no effect on their sound quality. Similarly, Pearl Drums positions the air vents on its Masters Premium models based on the golden ratio and claims that this arrangement improves bass response. Though Heinz Bohlen proposed the non-octave-repeating 833 cents scale based on combination tones, the tuning features relations based on the golden ratio. As a musical interval the ratio 1.618... is 833.090... cents (Play^ⓘ).

It has been claimed that many of Mozart's sonatas feature the golden ratio; though occasional divisions within his compositions approximate the golden section, there is no evidence they were intentional. In the early 1970s, Ernő Lendvai analyzed the compositions of Béla Bartók (1881–1945) based primarily on the golden ratio. For example, the fugue movement of Music for Strings, Percussion and Celesta crescendos at the golden mean, with other textural themes also utilizing successive Fibonacci numbers. Some music scholars have found the analysis dubious, and Lendvai himself points out Bartók's statement: "Let my music speak for itself; I lay no claim to any explanation of my works."

The golden ratio is also apparent in the organization of sections in the compositions of Claude Debussy (1862–1918). In Images, the first series in his Reflets dans l'eau, "the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position." Musicologist Roy Howat has observed that the formal boundaries of Debussy's La Mer correspond exactly to the golden section, as do Jardins sous la Pluie. Howat relies on the circumstantial evidence that he was associated to painters with knowledge of the golden ratio, and wrote to his publisher of a missing bar in Jardins sous la Pluie as symbolizing "the divine number". Scholars acknowledge the possible influence of the golden ratio, but caution that no strong evidence suggests that this was intentional.

Joseph Schillinger (1895–1943) developed a system of composition which utilized Fibonacci intervals in some of its melodies; he viewed these as the musical counterpart to the elaborate harmony evident within nature. Mario Livio notes an increased use of the golden ratio in the works of some 20th-century composers due to a revival of interest in mathematics.

Kepler's idealized model of the inner Solar System

Nature

Further information: Patterns in nature

See also: Fibonacci number § Nature

Johannes Kepler's 1597 Mysterium Cosmographicum features an idealized heliocentric model of the Solar System based on nested Platonic solids. Kepler also used the Fibonacci sequence to explain the pentagonal form of some flowers, and wrote that:

... the image of man and woman stems from the divine proportion. In my opinion, the propagation of plants and the progenitive acts of animals are in the same ratio ...

Detail of Aeonium tabuliforme showing its parastichy

In 1837, Auguste Bravais and his brother Louis connected phyllotaxis ratios to the Fibonacci sequence, noting that the divergence angle of new leaves was 137.5 degrees (360°/φ), or the golden angle. In his 1854 book, Adolf Zeising also found the golden ratio in the arrangement of plant parts such as branches and leaf veins, animal skeletons, the branching of veins and nerves, the proportions of chemical compounds, and the geometry of crystals, and wrote of a universal law:

... in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.

Some have argued that many apparent manifestations of the golden ratio in nature, especially regarding animal dimensions, are fictitious. However, Mario Livio points out that the angular arrangement of petals in a rose are guided by the fractional portion of multiples of ϕ. In 1989, Paul Davies proved that rotating black holes transition between hot and cold when the square of their mass equals ϕ times that of their speed. Physics experiments in the 1990s demonstrated that magnetic fluids in a magnetic field repel each other in patterns tending toward the golden ratio. In 2010, the journal Science reported that the golden ratio is present at the atomic scale in the magnetic resonance of spins in cobalt niobate crystals.

Mathematics

Usually, the lowercase form of phi (φ or φ) is used to symbolize the golden ratio. Sometimes the uppercase form ($\Phi$) is used for the reciprocal of the golden ratio, 1/φ.

Irrationality

The golden ratio is an irrational number, and due to its nature as an infinite continued fraction, it is the most impossible irrational number to express as a simple fraction. Below are two short proofs of its irrationality:

Contradiction from an expression in lowest terms

If φ were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the integers have a lower bound, so φ cannot be rational.

Recall that:

the whole is the longer part plus the shorter part;

the whole is to the longer part as the longer part is to the shorter part.

If we call the whole n and the longer part m, then the second statement above becomes

n is to m as m is to n − m,

or, algebraically

${\frac {n}{m}}={\frac {m}{n-m}}.\qquad (*)$

To say that the golden ratio φ is rational means that φ is a fraction n/m where n and m are integers. We may take n/m to be in lowest terms and n and m to be positive. But if n/m is in lowest terms, then the identity labeled (*) above says m/(n − m) is in still lower terms. That is a contradiction that follows from the assumption that φ is rational.

By irrationality of √5

Another short proof—perhaps more commonly known—of the irrationality of the golden ratio makes use of the closure of rational numbers under addition and multiplication. If $\textstyle {\frac {1+{\sqrt {5}}}{2}}$ is rational, then $\textstyle 2\left({\frac {1+{\sqrt {5}}}{2}}\right)-1={\sqrt {5}}$ is also rational, which is a contradiction if it is already known that the square root of a non-square natural number is irrational.

Minimal polynomial

The golden ratio is also an algebraic number and even an algebraic integer. It has minimal polynomial

$x^{2}-x-1.$

Having degree 2, this polynomial actually has two roots, the other being the golden ratio conjugate.

Golden ratio conjugate

The conjugate root to the minimal polynomial x² − x − 1 is

$-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.61803\,39887\dots .$

The absolute value of this quantity (≈ 0.618) corresponds to the length ratio taken in reverse order (shorter segment length over longer segment length, b/a), and is sometimes referred to as the golden ratio conjugate. It is denoted here by the capital Phi ($\Phi$):

$\Phi ={1 \over \varphi }=\varphi ^{-1}=0.61803\,39887\ldots .$

Alternatively, $\Phi$ can be expressed as

$\Phi =\varphi -1=1.61803\,39887\ldots -1=0.61803\,39887\ldots .$

This illustrates the unique property of the golden ratio among positive numbers, that

${1 \over \varphi }=\varphi -1,$

or its inverse:

${1 \over \Phi }=\Phi +1.$

This means 0.61803...:1 = 1:1.61803....

Alternative forms

Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers

The formula φ = 1 + 1/φ can be expanded recursively to obtain a continued fraction for the golden ratio:

$\varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

and its reciprocal:

$\varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

The convergents of these continued fractions (1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ..., or 1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...) are ratios of successive Fibonacci numbers.

The equation φ² = 1 + φ likewise produces the continued square root, or infinite surd, form:

$\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}.$

An infinite series can be derived to express phi:

$\varphi ={\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}.$

Also:

$\varphi =1+2\sin(\pi /10)=1+2\sin 18^{\circ }$

$\varphi ={1 \over 2}\csc(\pi /10)={1 \over 2}\csc 18^{\circ }$

$\varphi =2\cos(\pi /5)=2\cos 36^{\circ }$

$\varphi =2\sin(3\pi /10)=2\sin 54^{\circ }.$

These correspond to the fact that the length of the diagonal of a regular pentagon is φ times the length of its side, and similar relations in a pentagram.

Geometry

The number φ turns up frequently in geometry, particularly in figures with pentagonal symmetry. The length of a regular pentagon's diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Odd numbered groups of golden rectangles fit perfectly into a square.

There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem). However, a useful approximation results from dividing the sphere into parallel bands of equal surface area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 360°/φ ≅ 222.5°. This method was used to arrange the 1500 mirrors of the student-participatory satellite Starshine-3.

Dividing a line segment by interior division according to the golden ratio

Dividing a line segment by interior division

1. Having a line segment AB, construct a perpendicular BC at point B, with BC half the length of AB. Draw the hypotenuse AC.
2. Draw an arc with center C and radius BC. This arc intersects the hypotenuse AC at point D.
3. Draw an arc with center A and radius AD. This arc intersects the original line segment AB at point S. Point S divides the original line segment AB into line segments AS and SB with lengths in the golden ratio.

Dividing a line segment by exterior division

Dividing a line segment by exterior division according to the golden ratio

1. Draw a line segment AS and construct off the point S a segment SC perpendicular to AS and with the same length as AS.
2. Do bisect the line segment AS with M.
3. A circular arc around M with radius MC intersects in point B the straight line through points A and S (also known as the extension of AS). The ratio of AS to the constructed segment SB is the golden ratio.

Application examples you can see in the articles Pentagon with a given side length, Decagon with given circumcircle and Decagon with a given side length.

Both the above displayed different algorithms produce geometric constructions that determine two aligned line segments where the ratio of the longer to the shorter one is the golden ratio.

Golden triangle, pentagon and pentagram

Golden triangle

The golden triangle can be characterized as an isosceles triangle ABC with the property that bisecting the angle C produces a new triangle CXB, which is a similar triangle to the original.

A golden triangle. The double-red-arched angle is 36 degrees,
or ${\frac {\pi }{5}}$ radians.

If angle BCX = α, then XCA = α because of the bisection, and CAB = α because of the similar triangles; ABC = 2α from the original isosceles symmetry, and BXC = 2α by similarity. The angles in a triangle add up to 180°, so 5α = 180, giving α = 36°. The angles of the golden triangle are thus 36°-72°-72°. The angles of the remaining obtuse isosceles triangle AXC (sometimes called the golden gnomon) are 36°-36°-108°.

Suppose XB has length 1, and we call BC length φ. Because of the isosceles triangles XC=XA and BC=XC, so these are also length φ. Length AC = AB, therefore equals φ + 1. But triangle ABC is similar to triangle CXB, so AC/BC = BC/BX, AC/φ = φ/1, and so AC also equals φ². Thus φ² = φ + 1, confirming that φ is indeed the golden ratio.

Similarly, the ratio of the area of the larger triangle AXC to the smaller CXB is equal to φ, while the inverse ratio is φ − 1.

Pentagon

In a regular pentagon the ratio of a diagonal to a side is the golden ratio, while intersecting diagonals section each other in the golden ratio.

A and B are midpoints of the sides EF and ED of an equilateral triangle DEF. Extend AB to meet the circumcircle of DEF at C.
${\tfrac {|AB|}{|BC|}}={\tfrac {|AC|}{|AB|}}=\phi$

Odom's construction

George Odom has given a remarkably simple construction for φ involving an equilateral triangle: if an equilateral triangle is inscribed in a circle and the line segment joining the midpoints of two sides is continued to intersect the circle, then these three points are in golden proportion. This result is a straightforward consequence of the intersecting chords theorem and can be used to construct a regular pentagon, a construction that attracted the attention of the noted geometer H. S. M. Coxeter, who published it in Odom's name as a diagram in the American Mathematical Monthly.

Pentagram

The golden ratio plays an important role in the geometry of pentagrams. Each intersection of edges sections other edges in the golden ratio. Also, the ratio of the length of the shorter segment to the segment bounded by the two intersecting edges (a side of the pentagon in the pentagram's center) is φ, as the four-color illustration shows.

The pentagram includes ten isosceles triangles: five acute and five obtuse isosceles triangles. In all of them, the ratio of the longer side to the shorter side is φ. The acute triangles are golden triangles. The obtuse isosceles triangles are golden gnomons.

Ptolemy's theorem

The golden ratio in a regular pentagon can be computed using Ptolemy's theorem.

The golden ratio properties of a regular pentagon can be confirmed by applying Ptolemy's theorem to the quadrilateral formed by removing one of its vertices. If the quadrilateral's long edge and diagonals are b, and short edges are a, then Ptolemy's theorem gives b² = a² + ab which yields

${b \over a}={{1+{\sqrt {5}}} \over 2}.$

Scalenity of triangles

Consider a triangle with sides of lengths a, b, and c in decreasing order. Define the "scalenity" of the triangle to be the smaller of the two ratios a/b and b/c. The scalenity is always less than φ and can be made as close as desired to φ.

Triangle whose sides form a geometric progression

A regular square pyramid is determined by its medial right triangle, whose edges are the pyramid's semi-base (b), height (h) and apothem (a).

If the side lengths of a triangle form a geometric progression and are in the ratio 1 : r : r², where r is the common ratio, then r must lie in the range φ−1 < r < φ, which is a consequence of the triangle inequality (the sum of any two sides of a triangle must be strictly bigger than the length of the third side). If r = φ then the shorter two sides are 1 and φ but their sum is φ², thus r < φ. A similar calculation shows that r > φ−1. A triangle whose sides are in the ratio 1 : √φ : φ is a right triangle (because 1 + φ = φ²) known as a Kepler triangle.

Golden pyramid

A square pyramid in which the apothem (slant height along the bisector of a face) is equal to φ times the semi-base (half the base width) has golden ratio properties. The isosceles triangle that is the face of such a pyramid can be constructed from the two halves of a diagonally split golden rectangle (of size apothem by semi-base). The height of this pyramid is ${\sqrt {\varphi }}$ times the semi-base, and the medial right triangle of the pyramid is a Kepler triangle, with sides $1:{\sqrt {\varphi }}:\varphi$. This right triangle's edge lengths are in geometric progression.

The Great Pyramid of Giza (c. 2560 BC) closely approximates such a pyramid.

A rhombic triacontahedron

Golden triangle, rhombus, and rhombic triacontahedron

A golden rhombus is a rhombus whose diagonals are in the golden ratio. The rhombic triacontahedron is a convex polytope that has a very special property: all of its faces are golden rhombi. In the rhombic triacontahedron, the dihedral angle between any two adjacent rhombi is 144°, which is twice the isosceles angle of a golden triangle and four times its most acute angle.

Relation to Fibonacci sequence

The mathematics of the golden ratio and of the Fibonacci sequence are intimately interconnected. The Fibonacci sequence is:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...

A closed-form expression for the Fibonacci sequence involves the golden ratio:

$F\left(n\right)={{\varphi ^{n}-(1-\varphi )^{n}} \over {\sqrt {5}}}={{\varphi ^{n}-(-\varphi )^{-n}} \over {\sqrt {5}}}.$

The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence (or any Fibonacci-like sequence), as originally shown by Kepler:

$\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .$

In other words, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge to φ as the Fibonacci numbers increase, and:

$\sum _{n=1}^{\infty }|F_{n}\varphi -F_{n+1}|=\varphi .$

More generally:

$\lim _{n\to \infty }{\frac {F_{n+a}}{F_{n}}}=\varphi ^{a},$

where above, the ratios of consecutive terms of the Fibonacci sequence, is a case when $a=1.$

Furthermore, the successive powers of φ obey the Fibonacci recurrence:

$\varphi ^{n+1}=\varphi ^{n}+\varphi ^{n-1}.$

This identity allows any polynomial in φ to be reduced to a linear expression. For example:

${\begin{aligned}3\varphi ^{3}-5\varphi ^{2}+4&=3(\varphi ^{2}+\varphi )-5\varphi ^{2}+4\\&=3[(\varphi +1)+\varphi ]-5(\varphi +1)+4\\&=\varphi +2\approx 3.618.\end{aligned}}$

The reduction to a linear expression can be accomplished in one step by using the relationship

$\varphi ^{k}=F_{k}\varphi +F_{k-1},$

where $F_{k}$ is the kth Fibonacci number.

However, this is no special property of φ, because polynomials in any solution x to a quadratic equation can be reduced in an analogous manner, by applying:

$x^{2}=ax+b$

for given coefficients a, b such that x satisfies the equation. Even more generally, any rational function (with rational coefficients) of the root of an irreducible nth-degree polynomial over the rationals can be reduced to a polynomial of degree n ‒ 1. Phrased in terms of field theory, if α is a root of an irreducible nth-degree polynomial, then $\mathbb {Q} (\alpha )$ has degree n over $\mathbb {Q}$, with basis $\{1,\alpha ,\dots ,\alpha ^{n-1}\}.$

Symmetries

The golden ratio and inverse golden ratio $\varphi _{\pm }=(1\pm {\sqrt {5}})/2$ have a set of symmetries that preserve and interrelate them. They are both preserved by the fractional linear transformations $x,1/(1-x),(x-1)/x,$ – this fact corresponds to the identity and the definition quadratic equation. Further, they are interchanged by the three maps $1/x,1-x,x/(x-1)$ – they are reciprocals, symmetric about $1/2$, and (projectively) symmetric about 2.

More deeply, these maps form a subgroup of the modular group $\operatorname {PSL} (2,\mathbf {Z} )$ isomorphic to the symmetric group on 3 letters, $S_{3},$ corresponding to the stabilizer of the set $\{0,1,\infty \}$ of 3 standard points on the projective line, and the symmetries correspond to the quotient map $S_{3}\to S_{2}$ – the subgroup $C_{3}<S_{3}$ consisting of the 3-cycles and the identity $()(01\infty )(0\infty 1)$ fixes the two numbers, while the 2-cycles interchange these, thus realizing the map.

Other properties

The golden ratio has the simplest expression (and slowest convergence) as a continued fraction expansion of any irrational number (see Alternate forms above). It is, for that reason, one of the worst cases of Lagrange's approximation theorem and it is an extremal case of the Hurwitz inequality for Diophantine approximations. This may be why angles close to the golden ratio often show up in phyllotaxis (the growth of plants).

The defining quadratic polynomial and the conjugate relationship lead to decimal values that have their fractional part in common with φ:

$\varphi ^{2}=\varphi +1=2.618\dots$

${1 \over \varphi }=\varphi -1=0.618\dots .$

The sequence of powers of φ contains these values 0.618..., 1.0, 1.618..., 2.618...; more generally, any power of φ is equal to the sum of the two immediately preceding powers:

$\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}=\varphi \cdot \operatorname {F} _{n}+\operatorname {F} _{n-1}.$

As a result, one can easily decompose any power of φ into a multiple of φ and a constant. The multiple and the constant are always adjacent Fibonacci numbers. This leads to another property of the positive powers of φ:

If $\lfloor n/2-1\rfloor =m$, then:

$\!\ \varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-3}+\cdots +\varphi ^{n-1-2m}+\varphi ^{n-2-2m}$

$\!\ \varphi ^{n}-\varphi ^{n-1}=\varphi ^{n-2}.$

When the golden ratio is used as the base of a numeral system (see Golden ratio base, sometimes dubbed phinary or φ-nary), every integer has a terminating representation, despite φ being irrational, but every fraction has a non-terminating representation.

The golden ratio is a fundamental unit of the algebraic number field $\mathbb {Q} ({\sqrt {5}})$ and is a Pisot–Vijayaraghavan number. In the field $\mathbb {Q} ({\sqrt {5}})$, where $L_{n}$ is the $n$-th Lucas number, we have:

$\varphi ^{n}={{L_{n}+F_{n}{\sqrt {5}}} \over 2}$.

The golden ratio also appears in hyperbolic geometry, as the maximum distance from a point on one side of an ideal triangle to the closer of the other two sides: this distance, the side length of the equilateral triangle formed by the points of tangency of a circle inscribed within the ideal triangle, is $4\log(\varphi )$.

Decimal expansion

The golden ratio's decimal expansion can be calculated directly from the expression

$\varphi ={1+{\sqrt {5}} \over 2}$

with √5 ≈ 2.2360679774997896964 OEIS: A002163. The square root of 5 can be calculated with the Babylonian method, starting with an initial estimate such as xφ = 2 and iterating

$x_{n+1}={\frac {(x_{n}+5/x_{n})}{2}}$

for n = 1, 2, 3, ..., until the difference between x_n and x_n−1 becomes zero, to the desired number of digits.

The Babylonian algorithm for √5 is equivalent to Newton's method for solving the equation x² − 5 = 0. In its more general form, Newton's method can be applied directly to any algebraic equation, including the equation x² − x − 1 = 0 that defines the golden ratio. This gives an iteration that converges to the golden ratio itself,

$x_{n+1}={\frac {x_{n}^{2}+1}{2x_{n}-1}},$

for an appropriate initial estimate xφ such as xφ = 1. A slightly faster method is to rewrite the equation as x − 1 − 1/x = 0, in which case the Newton iteration becomes

$x_{n+1}={\frac {x_{n}^{2}+2x_{n}}{x_{n}^{2}+1}}.$

These iterations all converge quadratically; that is, each step roughly doubles the number of correct digits. The golden ratio is therefore relatively easy to compute with arbitrary precision. The time needed to compute n digits of the golden ratio is proportional to the time needed to divide two n-digit numbers. This is considerably faster than known algorithms for the transcendental numbers π and e.

An easily programmed alternative using only integer arithmetic is to calculate two large consecutive Fibonacci numbers and divide them. The ratio of Fibonacci numbers F ₂₅₀₀₁ and F ₂₅₀₀₀, each over 5000 digits, yields over 10,000 significant digits of the golden ratio.

The decimal expansion of the golden ratio φ has been calculated to an accuracy of two trillion (2×10¹² = 2,000,000,000,000) digits.

Disputed claims

Many attempts have been made to link objects to the golden ratio which lack specificity or evidence to back them. Examples of discredited observations of the golden ratio include the following:

Nautilus shells are often erroneously claimed to be golden-proportioned.

• Some specific proportions in the bodies of many animals (including humans) and parts of the shells of mollusks are often claimed to be in the golden ratio. There is a large variation in the real measures of these elements in specific individuals, however, and the proportion in question is often significantly different from the golden ratio. The ratio of successive phalangeal bones of the digits and the metacarpal bone has been said to approximate the golden ratio. The nautilus shell, the construction of which proceeds in a logarithmic spiral, is often cited, usually with the claim that such a spiral is related to the golden ratio, or that successive chambers are proportioned by it; however, actual measurements do not support this claim.
• In the mid-nineteenth century, Friedrich Röber theorized that various Egyptian pyramids were related to the Kepler triangle and some of Euclid's propositions, specifically claiming that either their whole or half-side lengths are related to their heights by the golden ratio. However, Röber agreed with John Shae Perring that the side-to-height ratio of the Great Pyramid of Giza is the rational 8:5. In 1859, John Taylor misinterpreted Herodotus (c. 440 BC) as indicating that the Great Pyramid's height squared equals the area of one of its face triangles, which would make it seem to incorporate the Kepler triangle. Based on some measurements, the slant height of one of the Great Pyramid's faces divided by its semi-base approximates φ; together with its height, the three lengths do in fact resemble a Kepler triangle. However, most modern historians of science contend that "it is highly unlikely that either the ancient Babylonians or the ancient Egyptians discovered the Golden Ratio and its properties."

Many of the proportions of the Parthenon have been theorized to exhibit the golden ratio, but this has largely been discredited.

• The Parthenon's façade (432 BC) has been said by some to contain golden ratio properties, but this has been discredited by other scholars. Keith Devlin says, "Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. ... The one thing we know for sure is that Euclid, in his famous textbook Elements, written around 300 BC, showed how to calculate its value." One researcher concluded that the golden ratio was totally absent from Greek architecture of the classical fifth century BC, and almost absent during the following six centuries, based on measurements of 15 temples, 18 monumental tombs, 8 sarcophagi, and 58 grave stelae.
• Historian John Man states that the pages of the Gutenberg Bible were based on the golden section. However, according to his own measurements, the ratio of height to width is 1.45.
• Inspired by the ideas of Adolf Zeising, psychologist Gustav Fechner devised a poll to test whether the golden ratio plays a role in the human perception of beauty. While Fechner found a preference amongst those he polled for golden rectangles, later attempts to test such a hypothesis have been inconclusive.
• The Section d'Or ('Golden Section') was a collective of painters, sculptors, poets and critics associated with Cubism and Orphism. Active from 1911 to around 1914, they adopted the name both to highlight that Cubism represented the continuation of a grand tradition, rather than being an isolated movement, and in homage to the mathematical harmony associated with Georges Seurat. However, despite this general interest in mathematical harmony, whether the paintings featured in the celebrated 1912 Salon de la Section d'Or exhibition used the golden ratio in any compositions is more difficult to determine. Mario Livio, for example, claims that they did not, and Marcel Duchamp said as much in an interview. On the other hand, an analysis by Camfield suggests that Juan Gris made use of the golden ratio in composing works that were likely, but not definitively, shown at the exhibition.
• In her 1974 book Life with the Painters of La Ruche, Marie Vorobieff implies that several Cubist friends of hers including Pablo Picasso and Diego Rivera used the golden ratio, although Livio notes that she "does not give any specific examples and some of her historical comments are inaccurate."
• Piet Mondrian has been said by some to have used the golden section extensively in his geometrical paintings, though other experts including Yve-Alain Bois have discredited these claims.
• In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio. The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers (e.g. Elliott wave principle and Fibonacci retracement). However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.

See also

• Donald in Mathmagic Land
• Golden angle
• Golden-section search
• List of works designed with the golden ratio
• Plastic number
• Sacred geometry
• Silver ratio
• Supergolden ratio

References

Footnotes

Citations

Works cited

• Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. ISBN 978-0-7679-0816-0.
• Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. ISBN 9-781-61614-424-1.
• Stakhov, Alexey P.; Olsen, Scott (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. Singapore: World Scientific Publishing. ISBN 978-981-277-582-5.

Further reading

• Doczi, György (2005) [1981]. The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala Publications. ISBN 978-1-59030-259-0.
• Gazalé, Midhat J. (1999), Gnomon: From Pharaohs to Fractals, Princeton University Press, ISBN 9780691005140
• Hambidge, Jay (1920). Dynamic Symmetry: The Greek Vase, New Haven CT: Yale University Press
• Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. ISBN 978-1-4027-3522-6.
• Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover Publications. ISBN 978-0-486-22254-7.
• Joseph, George G. (2000) [1991]. The Crest of the Peacock: The Non-European Roots of Mathematics (New ed.). Princeton, NJ: Princeton University Press. ISBN 978-0-691-00659-8.
• Sahlqvist, Leif (2008). Cardinal Alignments and the Golden Section: Principles of Ancient Cosmography and Design (3rd Rev. ed.). Charleston, SC: BookSurge. ISBN 978-1-4196-2157-4.
• Schneider, Michael S. (1994). A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. New York: HarperCollins. ISBN 978-0-06-016939-8.
• Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0.
• Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 978-0-88385-534-8.

External links

• "Golden ratio", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
• Golden Section in Photography: Golden Ratio, Golden Triangles, Golden Spiral
• Weisstein, Eric W. "Golden Ratio". MathWorld.
• Quotes about the Golden Ratio
• "Researcher explains mystery of golden ratio". PhysOrg. December 21, 2009..
• Knott, Ron. "The Golden section ratio: Phi". Information and activities by a mathematics professor.
• The Pentagram & The Golden Ratio. Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.
• Schneider, Robert P. (2011). "A Golden Pair of Identities in the Theory of Numbers". arXiv:1109.3216 [math.HO]. Proves formulas that involve the golden mean and the Euler totient and Möbius functions.
• The Myth That Will Not Go Away, by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.

Category:Euclidean plane geometry Category:Quadratic irrational numbers Category:Mathematical constants Category:History of geometry Category:Visual arts theory Category:Composition in visual art