In plane Euclidean geometry, a rhombus (pl.: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet[1]—also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle.
| Rhombus | |
|---|---|
 A rhombus in two different orientations | |
| Type | quadrilateral, trapezoid, parallelogram, kite |
| Edges and vertices | 4 |
| Schläfli symbol | { } + { } {2α} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D2), [2], (*22), order 4 |
| Area | (half the product of the diagonals) |
| Properties | convex, isotoxal |
| Dual polygon | rectangle |
Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square.[2]
Etymology
The word "rhombus" comes from Ancient Greek: ῥόμβος, romanized: rhómbos, meaning something that spins,[3] which derives from the verb ῥέμβω, romanized: rhémbō, meaning "to turn round and round."[4] The word was used both by Euclid and Archimedes, who used the term "solid rhombus" for a bicone, two right circular cones sharing a common base.[5]
The surface we refer to as rhombus today is a cross section of the bicone on a plane through the apexes of the two cones.
Characterizations
A simple (non-self-intersecting) quadrilateral is a rhombus if and only if it is any one of the following:[6][7]
- a parallelogram in which a diagonal bisects an interior angle
- a parallelogram in which at least two consecutive sides are equal in length
- a parallelogram in which the diagonals are perpendicular (an orthodiagonal parallelogram)
- a quadrilateral with four sides of equal length (by definition)
- a quadrilateral in which the diagonals are perpendicular and bisect each other
- a quadrilateral in which each diagonal bisects two opposite interior angles
- a quadrilateral ABCD possessing a point P in its plane such that the four triangles ABP, BCP, CDP, and DAP are all congruent[8]
- a quadrilateral ABCD in which the incircles in triangles ABC, BCD, CDA and DAB have a common point[9]
Basic properties
Every rhombus has two diagonals connecting pairs of opposite vertices, and two pairs of parallel sides. Using congruent triangles, one can prove that the rhombus is symmetric across each of these diagonals. It follows that any rhombus has the following properties:
- Opposite angles of a rhombus have equal measure.
- The two diagonals of a rhombus are perpendicular; that is, a rhombus is an orthodiagonal quadrilateral.
- Its diagonals bisect opposite angles.
The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram: for example, opposite sides are parallel; adjacent angles are supplementary; the two diagonals bisect one another; any line through the midpoint bisects the area; and the sum of the squares of the sides equals the sum of the squares of the diagonals (the parallelogram law). Thus denoting the common side as a and the diagonals as p and q, in every rhombus
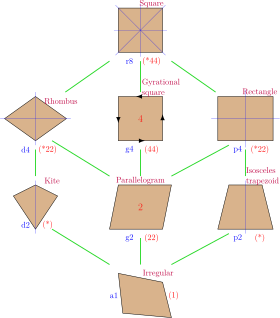
Not every parallelogram is a rhombus, though any parallelogram with perpendicular diagonals (the second property) is a rhombus. In general, any quadrilateral with perpendicular diagonals, one of which is a line of symmetry, is a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.
A rhombus is a tangential quadrilateral.[10] That is, it has an inscribed circle that is tangent to all four sides.
Diagonals
The length of the diagonals p = AC and q = BD can be expressed in terms of the rhombus side a and one vertex angle α as
and
These formulas are a direct consequence of the law of cosines.
Inradius
The inradius (the radius of a circle inscribed in the rhombus), denoted by r, can be expressed in terms of the diagonals p and q as[10]
or in terms of the side length a and any vertex angle α or β as
Area
As for all parallelograms, the area K of a rhombus is the product of its base and its height (h). The base is simply any side length a:
The area can also be expressed as the base squared times the sine of any angle:
or in terms of the height and a vertex angle:
or as half the product of the diagonals p, q:
or as the semiperimeter times the radius of the circle inscribed in the rhombus (inradius):
Another way, in common with parallelograms, is to consider two adjacent sides as vectors, forming a bivector, so the area is the magnitude of the bivector (the magnitude of the vector product of the two vectors), which is the determinant of the two vectors' Cartesian coordinates: K = x1y2 – x2y1.[11]
Dual properties
The dual polygon of a rhombus is a rectangle:[12]
- A rhombus has all sides equal, while a rectangle has all angles equal.
- A rhombus has opposite angles equal, while a rectangle has opposite sides equal.
- A rhombus has an inscribed circle, while a rectangle has a circumcircle.
- A rhombus has an axis of symmetry through each pair of opposite vertex angles, while a rectangle has an axis of symmetry through each pair of opposite sides.
- The diagonals of a rhombus intersect at equal angles, while the diagonals of a rectangle are equal in length.
- The figure formed by joining the midpoints of the sides of a rhombus is a rectangle, and vice versa.
Cartesian equation
The sides of a rhombus centered at the origin, with diagonals each falling on an axis, consist of all points (x, y) satisfying
The vertices are at and This is a special case of the superellipse, with exponent 1.
Other properties
- One of the five 2D lattice types is the rhombic lattice, also called centered rectangular lattice.
- Identical rhombi can tile the 2D plane in three different ways, including, for the 60° rhombus, the rhombille tiling.
| As topological square tilings | As 30-60 degree rhombille tiling | |
|---|---|---|
- Three-dimensional analogues of a rhombus include the bipyramid and the bicone as a surface of revolution.
As the faces of a polyhedron
Convex polyhedra with rhombi include the infinite set of rhombic zonohedrons, which can be seen as projective envelopes of hypercubes.
- A rhombohedron (also called a rhombic hexahedron) is a three-dimensional figure like a cuboid (also called a rectangular parallelepiped), except that its 3 pairs of parallel faces are up to 3 types of rhombi instead of rectangles.
- The rhombic dodecahedron is a convex polyhedron with 12 congruent rhombi as its faces.
- The rhombic triacontahedron is a convex polyhedron with 30 golden rhombi (rhombi whose diagonals are in the golden ratio) as its faces.
- The great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron with 30 intersecting rhombic faces.
- The rhombic hexecontahedron is a stellation of the rhombic triacontahedron. It is nonconvex with 60 golden rhombic faces with icosahedral symmetry.
- The rhombic enneacontahedron is a polyhedron composed of 90 rhombic faces, with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim ones.
- The rhombic icosahedron is a polyhedron composed of 20 rhombic faces, of which three, four, or five meet at each vertex. It has 10 faces on the polar axis with 10 faces following the equator.
| Isohedral | Isohedral golden rhombi | 2-isohedral | 3-isohedral | ||
|---|---|---|---|---|---|
| Trigonal trapezohedron | Rhombic dodecahedron | Rhombic triacontahedron | Rhombic icosahedron | Rhombic enneacontahedron | Rhombohedron |
See also
- Merkel-Raute
- Rhombus of Michaelis, in human anatomy
- Rhomboid, either a parallelepiped or a parallelogram that is neither a rhombus nor a rectangle
- Rhombic antenna
- Rhombic Chess
- Flag of the Department of North Santander of Colombia, containing four stars in the shape of a rhombus
- Superellipse (includes a rhombus with rounded corners)
References
- ^ Alsina, Claudi; Nelsen, Roger B. (31 December 2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. American Mathematical Soc. ISBN 9781614442165.
- ^ Note: Euclid's original definition and some English dictionaries' definition of rhombus excludes squares, but modern mathematicians prefer the inclusive definition. See, e.g., De Villiers, Michael (February 1994). "The role and function of a hierarchical classification of quadrilaterals". For the Learning of Mathematics. 14 (1): 11–18. JSTOR 40248098.
- ^ ῥόμβος Archived 2013-11-08 at the Wayback Machine, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ ρέμβω Archived 2013-11-08 at the Wayback Machine, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ "The Origin of Rhombus". Archived from the original on 2015-04-02. Retrieved 2005-01-25.
- ^ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition Archived 2020-02-26 at the Wayback Machine", Information Age Publishing, 2008, pp. 55-56.
- ^ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry Archived 2019-09-01 at the Wayback Machine, Mathematical Association of America, 2010, p. 53.
- ^ Paris Pamfilos (2016), "A Characterization of the Rhombus", Forum Geometricorum 16, pp. 331–336, [1] Archived 2016-10-23 at the Wayback Machine
- ^ "IMOmath, "26-th Brazilian Mathematical Olympiad 2004"" (PDF). Archived (PDF) from the original on 2016-10-18. Retrieved 2020-01-06.
- ^ a b Weisstein, Eric W. "Rhombus". MathWorld.
- ^ WildLinAlg episode 4 Archived 2017-02-05 at the Wayback Machine, Norman J Wildberger, Univ. of New South Wales, 2010, lecture via youtube
- ^ de Villiers, Michael, "Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette 95, March 2011, 102-107.
External links
- Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
- Rhombus definition, Math Open Reference with interactive applet.
- Rhombus area, Math Open Reference - shows three different ways to compute the area of a rhombus, with interactive applet
