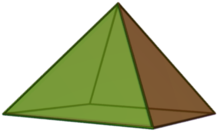
In geometry, a square pyramid is a pyramid with a square base, having a total of five faces. If the apex of the pyramid is directly above the center of the square, it is a right square pyramid with four isosceles triangles; otherwise, it is an oblique square pyramid. When all of the pyramid's edges are equal in length, its triangles are all equilateral, and it is called an equilateral square pyramid.
| Square pyramid | |
|---|---|
 | |
| Type | Pyramid, Johnson J92 – J1 – J2 |
| Faces | 4 triangles 1 square |
| Edges | 8 |
| Vertices | 5 |
| Vertex configuration | [1] |
| Symmetry group | |
| Volume | |
| Dual polyhedron | self-dual[2] |
| Properties | convex |
| Net | |
 | |
Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids, and many other similar buildings. They also occur in chemistry in square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches.
Properties edit
Right square pyramid edit
A square pyramid has five vertices, eight edges, and five faces. One face, called the base of the pyramid, is a square; the four other faces are triangles.[3] Four of the edges make up the square by connecting its four vertices. The other four edges are known as the lateral edges of the pyramid; they meet at the fifth vertex, called the apex.[4] If the pyramid's apex lies on a line erected perpendicularly from the center of the square, it is called a right square pyramid, and the four triangular faces are isosceles triangles. Otherwise, the pyramid has two or more non-isosceles triangular faces and is called an oblique square pyramid.[5]
The slant height of a right square pyramid is defined as the height of one of its isosceles triangles. It can be obtained via the Pythagorean theorem:
Many mathematicians have discovered the formula for calculating the volume of a square pyramid in ancient times. In the Moscow Mathematical Papyrus, Egyptian mathematicians demonstrated knowledge of the formula for calculating the volume of a truncated square pyramid, suggesting that they were also acquainted with the volume of a square pyramid, but it is unknown how the formula was derived. Beyond the discovery of the volume of a square pyramid, the problem of finding the slope and height of a square pyramid can be found in the Rhind Mathematical Papyrus.[11] The Babylonian mathematicians also considered the volume of a frustum, but gave an incorrect formula for it.[12] One Chinese mathematician Liu Hui also discovered the volume by the method of dissecting a rectangular solid into pieces.[13]
Equilateral square pyramid edit
If all triangular edges are of equal length, the four triangles are equilateral, and the pyramid's faces are all regular polygons, it is an equilateral square pyramid.[14] The dihedral angles between adjacent triangular faces are , and that between the base and each triangular face being half of that, .[1] A convex polyhedron with only regular polygons as faces is called a Johnson solid, and the equilateral square pyramid is the first Johnson solid, enumerated as .[15] Like other right pyramids with a regular polygon as a base, a right square pyramid has pyramidal symmetry. For the square pyramid, this is the symmetry of cyclic group : the pyramid is left invariant by rotations of one-, two-, and three-quarters of a full turn around its axis of symmetry, the line connecting the apex to the center of the base. It is also mirror symmetric relative to any perpendicular plane passing through a bisector of the base.[1] It can be represented as the wheel graph ; more generally, a wheel graph is the representation of the skeleton of a -sided pyramid.[16]
Because its edges are all equal in length (that is, ), its slant, height, surface area, and volume can be derived by substituting the formulas of a right square pyramid:[17]
Applications edit
In architecture, the pyramids built in ancient Egypt are examples of buildings shaped like square pyramids.[18] Pyramidologists have put forward various suggestions for the design of the Great Pyramid of Giza, including a theory based on the Kepler triangle and the golden ratio. However, modern scholars favor descriptions using integer ratios, as being more consistent with the knowledge of Egyptian mathematics and proportion.[19] The Mesoamerican pyramids are also ancient pyramidal buildings similar to the Egyptian; they differ in having flat tops and stairs ascending their faces.[20] Modern buildings whose designs imitate the Egyptian pyramids include the Louvre Pyramid and the casino hotel Luxor Las Vegas.[21]
In stereochemistry, an atom cluster can have a square pyramidal geometry. A square pyramidal molecule has a main-group element with one active lone pair, which can be described by a model that predicts the geometry of molecules known as VSEPR theory.[22] Examples of molecules with this structure include chlorine pentafluoride, bromine pentafluoride, and iodine pentafluoride.[23]
The base of a square pyramid can be attached to a square face of another polyhedron to construct new polyhedra, an example of augmentation. For example, a tetrakis hexahedron can be constructed by attaching the base of an equilateral square pyramid onto each face of a cube.[24] Attaching prisms or antiprisms to pyramids is known as elongation or gyroelongation, respectively.[25] Some of the other Johnson solids can be constructed by either augmenting square pyramids or augmenting other shapes with square pyramids: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism , augmented pentagonal prism , biaugmented pentagonal prism , augmented hexagonal prism , parabiaugmented hexagonal prism , metabiaugmented hexagonal prism , triaugmented hexagonal prism , and augmented sphenocorona .[26]
See also edit
- Square pyramidal number, a natural number that counts the number of stacked spheres in a square pyramid.
Notes edit
- ^ a b c Johnson (1966).
- ^ Wohlleben (2019), p. 485–486.
- ^ Clissold (2020), p. 180.
- ^ O'Keeffe & Hyde (2020), p. 141; Smith (2000), p. 98.
- ^ Freitag (2014), p. 598.
- ^ Larcombe (1929), p. 177; Perry & Perry (1981), pp. 145–146.
- ^ Larcombe (1929), p. 177.
- ^ Freitag (2014), p. 798.
- ^ Alexander & Koeberlin (2014), p. 403.
- ^ Larcombe (1929), p. 178.
- ^ Cromwell (1997), pp. 20–22.
- ^ Eves (1997), p. 2.
- ^ Wagner (1979).
- ^ Hocevar (1903), p. 44.
- ^ Uehara (2020), p. 62.
- ^ Pisanski & Servatius (2013), p. 21.
- ^ Simonson (2011), p. 123; Berman (1971), see table IV, line 21.
- ^ Kinsey, Moore & Prassidis (2011), p. 371.
- ^ Herz-Fischler (2000) surveys many alternative theories for this pyramid's shape. See Chapter 11, "Kepler triangle theory", pp. 80–91, for material specific to the Kepler triangle, and p. 166 for the conclusion that the Kepler triangle theory can be eliminated by the principle that "A theory must correspond to a level of mathematics consistent with what was known to the ancient Egyptians." See note 3, p. 229, for the history of Kepler's work with this triangle. See Rossi (2004), pp. 67–68, quoting that "there is no direct evidence in any ancient Egyptian written mathematical source of any arithmetic calculation or geometrical construction which could be classified as the Golden Section ... convergence to , and itself as a number, do not fit with the extant Middle Kingdom mathematical sources"; see also extensive discussion of multiple alternative theories for the shape of the pyramid and other Egyptian architecture, pp. 7–56. See also Rossi & Tout (2002) and Markowsky (1992).
- ^ Feder (2010), p. 34; Takacs & Cline (2015), p. 16.
- ^ Jarvis & Naested (2012), p. 172; Simonson (2011), p. 122.
- ^ Petrucci, Harwood & Herring (2002), p. 414.
- ^ Emeléus (1969), p. 13.
- ^ Demey & Smessaert (2017).
- ^ Slobodan, Obradović & Ðukanović (2015).
- ^ Rajwade (2001), pp. 84–89. See Table 12.3, where denotes the -sided prism and denotes the -sided antiprism.
References edit
- Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. ISBN 978-1-285-19569-8.
- Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- Clissold, Caroline (2020). Maths 5–11: A Guide for Teachers. Taylor & Francis. ISBN 978-0-429-26907-3.
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 978-0-521-55432-9.
- Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation". Symmetry. 9 (10): 204. Bibcode:2017Symm....9..204D. doi:10.3390/sym9100204.
- Emeléus, H. J. (1969). The Chemistry of Fluorine and Its Compounds. Academic Press. ISBN 978-1-4832-7304-4.
- Eves, Howard (1997). Foundations and Fundamental Concepts of Mathematics (3rd ed.). Dover Publications. ISBN 978-0-486-69609-6.
- Feder, Kenneth L. (2010). Encyclopedia of Dubious Archaeology: From Atlantis to the Walam Olum: From Atlantis to the Walam Olum. ABC-CLIO. ISBN 978-0-313-37919-2.
- Freitag, Mark A. (2014). Mathematics for Elementary School Teachers: A Process Approach. Brooks/Cole. ISBN 978-0-618-61008-2.
- Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5.
- Hocevar, Franx (1903). Solid Geometry. A. & C. Black.
- Jarvis, Daniel; Naested, Irene (2012). Exploring the Math and Art Connection: Teaching and Learning Between the Lines. Brush Education. ISBN 978-1-55059-398-3.
- Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
- Kinsey, L. Christine; Moore, Teresa E.; Prassidis, Efstratios (2011). Geometry and Symmetry. John Wiley & Sons. ISBN 978-0-470-49949-8.
- Larcombe, H. J. (1929). Cambridge Intermediate Mathematics: Geometry Part II. Cambridge University Press.
- Markowsky, George (1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1). Mathematical Association of America: 2–19. doi:10.2307/2686193. JSTOR 2686193. Retrieved 29 June 2012.
- O'Keeffe, Michael; Hyde, Bruce G. (2020). Crystal Structures: Patterns and Symmetry. Dover Publications. ISBN 978-0-486-83654-6.
- Perry, O. W.; Perry, J. (1981). Mathematics. Springer. doi:10.1007/978-1-349-05230-1. ISBN 978-1-349-05230-1.
- Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry: Principles and Modern Applications. Vol. 1. Prentice Hall. ISBN 978-0-13-014329-7.
- Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. doi:10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4.
- Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. pp. 67–68.
- Rossi, Corinna; Tout, Christopher A. (2002). "Were the Fibonacci series and the Golden Section known in ancient Egypt?". Historia Mathematica. 29 (2): 101–113. doi:10.1006/hmat.2001.2334. hdl:11311/997099.
- Simonson, Shai (2011). Rediscovering Mathematics: You Do the Math. Mathematical Association of America. ISBN 978-0-88385-912-4.
- Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.
- Smith, James T. (2000). Methods of Geometry. John Wiley & Sons. ISBN 0-471-25183-6.
- Takacs, Sarolta Anna; Cline, Eric H. (2015). The Ancient World. Routledge. p. 16. ISBN 978-1-317-45839-5.
- Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- Wagner, Donald Blackmore (1979). "An early Chinese derivation of the volume of a pyramid: Liu Hui, third century A.D.". Historia Mathematics. 6 (2): 164–188. doi:10.1016/0315-0860(79)90076-4.
- Wohlleben, Eva (2019). "Duality in Non-Polyhedral Bodies Part I: Polyliner". In Cocchiarella, Luigi (ed.). ICGG 2018 – Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary – Milan, Italy, August 3–7, 2018. International Conference on Geometry and Graphics. Springer. doi:10.1007/978-3-319-95588-9. ISBN 978-3-319-95588-9.
External links edit
- Weisstein, Eric W., "Square pyramid" ("Johnson solid") at MathWorld.
- Weisstein, Eric W. "Wheel graph". MathWorld.
- Square Pyramid – Interactive Polyhedron Model
- Virtual Reality Polyhedra georgehart.com: The Encyclopedia of Polyhedra (VRML model)


