In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points. The distance is measured by a function called a metric or distance function.[1] Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry.
The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another.
Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and therefore admit the structure of a metric space, including Riemannian manifolds, normed vector spaces, and graphs. In abstract algebra, the p-adic numbers arise as elements of the completion of a metric structure on the rational numbers. Metric spaces are also studied in their own right in metric geometry[2] and analysis on metric spaces.[3]
Many of the basic notions of mathematical analysis, including balls, completeness, as well as uniform, Lipschitz, and Hölder continuity, can be defined in the setting of metric spaces. Other notions, such as continuity, compactness, and open and closed sets, can be defined for metric spaces, but also in the even more general setting of topological spaces.
Definition and illustration edit
Motivation edit
To see the utility of different notions of distance, consider the surface of the Earth as a set of points. We can measure the distance between two such points by the length of the shortest path along the surface, "as the crow flies"; this is particularly useful for shipping and aviation. We can also measure the straight-line distance between two points through the Earth's interior; this notion is, for example, natural in seismology, since it roughly corresponds to the length of time it takes for seismic waves to travel between those two points.
The notion of distance encoded by the metric space axioms has relatively few requirements. This generality gives metric spaces a lot of flexibility. At the same time, the notion is strong enough to encode many intuitive facts about what distance means. This means that general results about metric spaces can be applied in many different contexts.
Like many fundamental mathematical concepts, the metric on a metric space can be interpreted in many different ways. A particular metric may not be best thought of as measuring physical distance, but, instead, as the cost of changing from one state to another (as with Wasserstein metrics on spaces of measures) or the degree of difference between two objects (for example, the Hamming distance between two strings of characters, or the Gromov–Hausdorff distance between metric spaces themselves).
Definition edit
Formally, a metric space is an ordered pair (M, d) where M is a set and d is a metric on M, i.e., a function
- The distance from a point to itself is zero:
- (Positivity) The distance between two distinct points is always positive:
- (Symmetry) The distance from x to y is always the same as the distance from y to x:
- The triangle inequality holds: This is a natural property of both physical and metaphorical notions of distance: you can arrive at z from x by taking a detour through y, but this will not make your journey any shorter than the direct path.
If the metric d is unambiguous, one often refers by abuse of notation to "the metric space M".
By taking all axioms except the second, one can show that distance is always non-negative:
Simple examples edit
The real numbers edit
The real numbers with the distance function given by the absolute difference form a metric space. Many properties of metric spaces and functions between them are generalizations of concepts in real analysis and coincide with those concepts when applied to the real line.
Metrics on Euclidean spaces edit
The Euclidean plane can be equipped with many different metrics. The Euclidean distance familiar from school mathematics can be defined by
The taxicab or Manhattan distance is defined by
The maximum, , or Chebyshev distance is defined by
In fact, these three distances, while they have distinct properties, are similar in some ways. Informally, points that are close in one are close in the others, too. This observation can be quantified with the formula
A radically different distance can be defined by setting
All of these metrics make sense on as well as .
Subspaces edit
Given a metric space (M, d) and a subset , we can consider A to be a metric space by measuring distances the same way we would in M. Formally, the induced metric on A is a function defined by
History edit
This section needs expansion with: Reasons for generalizing the Euclidean metric, first non-Euclidean metrics studied, consequences for mathematics. You can help by adding to it. (August 2011) |
In 1906 Maurice Fréchet introduced metric spaces in his work Sur quelques points du calcul fonctionnel[7] in the context of functional analysis: his main interest was in studying the real-valued functions from a metric space, generalizing the theory of functions of several or even infinitely many variables, as pioneered by mathematicians such as Cesare Arzelà. The idea was further developed and placed in its proper context by Felix Hausdorff in his magnum opus Principles of Set Theory, which also introduced the notion of a (Hausdorff) topological space.[8]
General metric spaces have become a foundational part of the mathematical curriculum.[9] Prominent examples of metric spaces in mathematical research include Riemannian manifolds and normed vector spaces, which are the domain of differential geometry and functional analysis, respectively.[10] Fractal geometry is a source of some exotic metric spaces. Others have arisen as limits through the study of discrete or smooth objects, including scale-invariant limits in statistical physics, Alexandrov spaces arising as Gromov–Hausdorff limits of sequences of Riemannian manifolds, and boundaries and asymptotic cones in geometric group theory. Finally, many new applications of finite and discrete metric spaces have arisen in computer science.
Basic notions edit
A distance function is enough to define notions of closeness and convergence that were first developed in real analysis. Properties that depend on the structure of a metric space are referred to as metric properties. Every metric space is also a topological space, and some metric properties can also be rephrased without reference to distance in the language of topology; that is, they are really topological properties.
The topology of a metric space edit
For any point x in a metric space M and any real number r > 0, the open ball of radius r around x is defined to be the set of points that are strictly less than distance r from x:
An open set is a set which is a neighborhood of all its points. It follows that the open balls form a base for a topology on M. In other words, the open sets of M are exactly the unions of open balls. As in any topology, closed sets are the complements of open sets. Sets may be both open and closed as well as neither open nor closed.
This topology does not carry all the information about the metric space. For example, the distances d1, d2, and d∞ defined above all induce the same topology on , although they behave differently in many respects. Similarly, with the Euclidean metric and its subspace the interval (0, 1) with the induced metric are homeomorphic but have very different metric properties.
Conversely, not every topological space can be given a metric. Topological spaces which are compatible with a metric are called metrizable and are particularly well-behaved in many ways: in particular, they are paracompact[11] Hausdorff spaces (hence normal) and first-countable.[a] The Nagata–Smirnov metrization theorem gives a characterization of metrizability in terms of other topological properties, without reference to metrics.
Convergence edit
Convergence of sequences in Euclidean space is defined as follows:
- A sequence (xn) converges to a point x if for every ε > 0 there is an integer N such that for all n > N, d(xn, x) < ε.
Convergence of sequences in a topological space is defined as follows:
- A sequence (xn) converges to a point x if for every open set U containing x there is an integer N such that for all n > N, .
In metric spaces, both of these definitions make sense and they are equivalent. This is a general pattern for topological properties of metric spaces: while they can be defined in a purely topological way, there is often a way that uses the metric which is easier to state or more familiar from real analysis.
Completeness edit
Informally, a metric space is complete if it has no "missing points": every sequence that looks like it should converge to something actually converges.
To make this precise: a sequence (xn) in a metric space M is Cauchy if for every ε > 0 there is an integer N such that for all m, n > N, d(xm, xn) < ε. By the triangle inequality, any convergent sequence is Cauchy: if xm and xn are both less than ε away from the limit, then they are less than 2ε away from each other. If the converse is true—every Cauchy sequence in M converges—then M is complete.
Euclidean spaces are complete, as is with the other metrics described above. Two examples of spaces which are not complete are (0, 1) and the rationals, each with the metric induced from . One can think of (0, 1) as "missing" its endpoints 0 and 1. The rationals are missing all the irrationals, since any irrational has a sequence of rationals converging to it in (for example, its successive decimal approximations). These examples show that completeness is not a topological property, since is complete but the homeomorphic space (0, 1) is not.
This notion of "missing points" can be made precise. In fact, every metric space has a unique completion, which is a complete space that contains the given space as a dense subset. For example, [0, 1] is the completion of (0, 1), and the real numbers are the completion of the rationals.
Since complete spaces are generally easier to work with, completions are important throughout mathematics. For example, in abstract algebra, the p-adic numbers are defined as the completion of the rationals under a different metric. Completion is particularly common as a tool in functional analysis. Often one has a set of nice functions and a way of measuring distances between them. Taking the completion of this metric space gives a new set of functions which may be less nice, but nevertheless useful because they behave similarly to the original nice functions in important ways. For example, weak solutions to differential equations typically live in a completion (a Sobolev space) rather than the original space of nice functions for which the differential equation actually makes sense.
Bounded and totally bounded spaces edit
A metric space M is bounded if there is an r such that no pair of points in M is more than distance r apart.[b] The least such r is called the diameter of M.
The space M is called precompact or totally bounded if for every r > 0 there is a finite cover of M by open balls of radius r. Every totally bounded space is bounded. To see this, start with a finite cover by r-balls for some arbitrary r. Since the subset of M consisting of the centers of these balls is finite, it has finite diameter, say D. By the triangle inequality, the diameter of the whole space is at most D + 2r. The converse does not hold: an example of a metric space that is bounded but not totally bounded is (or any other infinite set) with the discrete metric.
Compactness edit
Compactness is a topological property which generalizes the properties of a closed and bounded subset of Euclidean space. There are several equivalent definitions of compactness in metric spaces:
- A metric space M is compact if every open cover has a finite subcover (the usual topological definition).
- A metric space M is compact if every sequence has a convergent subsequence. (For general topological spaces this is called sequential compactness and is not equivalent to compactness.)
- A metric space M is compact if it is complete and totally bounded. (This definition is written in terms of metric properties and does not make sense for a general topological space, but it is nevertheless topologically invariant since it is equivalent to compactness.)
One example of a compact space is the closed interval [0, 1].
Compactness is important for similar reasons to completeness: it makes it easy to find limits. Another important tool is Lebesgue's number lemma, which shows that for any open cover of a compact space, every point is relatively deep inside one of the sets of the cover.
Functions between metric spaces edit
Unlike in the case of topological spaces or algebraic structures such as groups or rings, there is no single "right" type of structure-preserving function between metric spaces. Instead, one works with different types of functions depending on one's goals. Throughout this section, suppose that and are two metric spaces. The words "function" and "map" are used interchangeably.
Isometries edit
One interpretation of a "structure-preserving" map is one that fully preserves the distance function:
- A function is distance-preserving[12] if for every pair of points x and y in M1,
It follows from the metric space axioms that a distance-preserving function is injective. A bijective distance-preserving function is called an isometry.[13] One perhaps non-obvious example of an isometry between spaces described in this article is the map defined by
If there is an isometry between the spaces M1 and M2, they are said to be isometric. Metric spaces that are isometric are essentially identical.
Continuous maps edit
On the other end of the spectrum, one can forget entirely about the metric structure and study continuous maps, which only preserve topological structure. There are several equivalent definitions of continuity for metric spaces. The most important are:
- Topological definition. A function is continuous if for every open set U in M2, the preimage is open.
- Sequential continuity. A function is continuous if whenever a sequence (xn) converges to a point x in M1, the sequence converges to the point f(x) in M2.
- (These first two definitions are not equivalent for all topological spaces.)
- ε–δ definition. A function is continuous if for every point x in M1 and every ε > 0 there exists δ > 0 such that for all y in M1 we have
A homeomorphism is a continuous bijection whose inverse is also continuous; if there is a homeomorphism between M1 and M2, they are said to be homeomorphic. Homeomorphic spaces are the same from the point of view of topology, but may have very different metric properties. For example, is unbounded and complete, while (0, 1) is bounded but not complete.
Uniformly continuous maps edit
A function is uniformly continuous if for every real number ε > 0 there exists δ > 0 such that for all points x and y in M1 such that , we have
The only difference between this definition and the ε–δ definition of continuity is the order of quantifiers: the choice of δ must depend only on ε and not on the point x. However, this subtle change makes a big difference. For example, uniformly continuous maps take Cauchy sequences in M1 to Cauchy sequences in M2. In other words, uniform continuity preserves some metric properties which are not purely topological.
On the other hand, the Heine–Cantor theorem states that if M1 is compact, then every continuous map is uniformly continuous. In other words, uniform continuity cannot distinguish any non-topological features of compact metric spaces.
Lipschitz maps and contractions edit
A Lipschitz map is one that stretches distances by at most a bounded factor. Formally, given a real number K > 0, the map is K-Lipschitz if
A 1-Lipschitz map is sometimes called a nonexpanding or metric map. Metric maps are commonly taken to be the morphisms of the category of metric spaces.
A K-Lipschitz map for K < 1 is called a contraction. The Banach fixed-point theorem states that if M is a complete metric space, then every contraction admits a unique fixed point. If the metric space M is compact, the result holds for a slightly weaker condition on f: a map admits a unique fixed point if
Quasi-isometries edit
A quasi-isometry is a map that preserves the "large-scale structure" of a metric space. Quasi-isometries need not be continuous. For example, and its subspace are quasi-isometric, even though one is connected and the other is discrete. The equivalence relation of quasi-isometry is important in geometric group theory: the Švarc–Milnor lemma states that all spaces on which a group acts geometrically are quasi-isometric.[15]
Formally, the map is a quasi-isometric embedding if there exist constants A ≥ 1 and B ≥ 0 such that
Notions of metric space equivalence edit
Given two metric spaces and :
- They are called homeomorphic (topologically isomorphic) if there is a homeomorphism between them (i.e., a continuous bijection with a continuous inverse). If and the identity map is a homeomorphism, then and are said to be topologically equivalent.
- They are called uniformic (uniformly isomorphic) if there is a uniform isomorphism between them (i.e., a uniformly continuous bijection with a uniformly continuous inverse).
- They are called bilipschitz homeomorphic if there is a bilipschitz bijection between them (i.e., a Lipschitz bijection with a Lipschitz inverse).
- They are called isometric if there is a (bijective) isometry between them. In this case, the two metric spaces are essentially identical.
- They are called quasi-isometric if there is a quasi-isometry between them.
Metric spaces with additional structure edit
Normed vector spaces edit
A normed vector space is a vector space equipped with a norm, which is a function that measures the length of vectors. The norm of a vector v is typically denoted by . Any normed vector space can be equipped with a metric in which the distance between two vectors x and y is given by
- translation invariant: for every x, y, and a in X; and
- absolutely homogeneous: for every x and y in X and real number α;
then it is the metric induced by the norm
Among examples of metrics induced by a norm are the metrics d1, d2, and d∞ on , which are induced by the Manhattan norm, the Euclidean norm, and the maximum norm, respectively. More generally, the Kuratowski embedding allows one to see any metric space as a subspace of a normed vector space.
Infinite-dimensional normed vector spaces, particularly spaces of functions, are studied in functional analysis. Completeness is particularly important in this context: a complete normed vector space is known as a Banach space. An unusual property of normed vector spaces is that linear transformations between them are continuous if and only if they are Lipschitz. Such transformations are known as bounded operators.
Length spaces edit
A curve in a metric space (M, d) is a continuous function . The length of γ is measured by
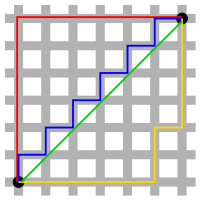
A geodesic metric space is a metric space which admits a geodesic between any two of its points. The spaces and are both geodesic metric spaces. In , geodesics are unique, but in , there are often infinitely many geodesics between two points, as shown in the figure at the top of the article.
The space M is a length space (or the metric d is intrinsic) if the distance between any two points x and y is the infimum of lengths of paths between them. Unlike in a geodesic metric space, the infimum does not have to be attained. An example of a length space which is not geodesic is the Euclidean plane minus the origin: the points (1, 0) and (-1, 0) can be joined by paths of length arbitrarily close to 2, but not by a path of length 2. An example of a metric space which is not a length space is given by the straight-line metric on the sphere: the straight line between two points through the center of the Earth is shorter than any path along the surface.
Given any metric space (M, d), one can define a new, intrinsic distance function dintrinsic on M by setting the distance between points x and y to be infimum of the d-lengths of paths between them. For instance, if d is the straight-line distance on the sphere, then dintrinsic is the great-circle distance. However, in some cases dintrinsic may have infinite values. For example, if M is the Koch snowflake with the subspace metric d induced from , then the resulting intrinsic distance is infinite for any pair of distinct points.
Riemannian manifolds edit
A Riemannian manifold is a space equipped with a Riemannian metric tensor, which determines lengths of tangent vectors at every point. This can be thought of defining a notion of distance infinitesimally. In particular, a differentiable path in a Riemannian manifold M has length defined as the integral of the length of the tangent vector to the path:
The Riemannian metric is uniquely determined by the distance function; this means that in principle, all information about a Riemannian manifold can be recovered from its distance function. One direction in metric geometry is finding purely metric ("synthetic") formulations of properties of Riemannian manifolds. For example, a Riemannian manifold is a CAT(k) space (a synthetic condition which depends purely on the metric) if and only if its sectional curvature is bounded above by k.[20] Thus CAT(k) spaces generalize upper curvature bounds to general metric spaces.
Metric measure spaces edit
Real analysis makes use of both the metric on and the Lebesgue measure. Therefore, generalizations of many ideas from analysis naturally reside in metric measure spaces: spaces that have both a measure and a metric which are compatible with each other. Formally, a metric measure space is a metric space equipped with a Borel regular measure such that every ball has positive measure.[21] For example Euclidean spaces of dimension n, and more generally n-dimensional Riemannian manifolds, naturally have the structure of a metric measure space, equipped with the Lebesgue measure. Certain fractal metric spaces such as the Sierpiński gasket can be equipped with the α-dimensional Hausdorff measure where α is the Hausdorff dimension. In general, however, a metric space may not have an "obvious" choice of measure.
One application of metric measure spaces is generalizing the notion of Ricci curvature beyond Riemannian manifolds. Just as CAT(k) and Alexandrov spaces generalize sectional curvature bounds, RCD spaces are a class of metric measure spaces which generalize lower bounds on Ricci curvature.[22]
Further examples and applications edit
Graphs and finite metric spaces edit
A metric space is discrete if its induced topology is the discrete topology. Although many concepts, such as completeness and compactness, are not interesting for such spaces, they are nevertheless an object of study in several branches of mathematics. In particular, finite metric spaces (those having a finite number of points) are studied in combinatorics and theoretical computer science.[23] Embeddings in other metric spaces are particularly well-studied. For example, not every finite metric space can be isometrically embedded in a Euclidean space or in Hilbert space. On the other hand, in the worst case the required distortion (bilipschitz constant) is only logarithmic in the number of points.[24][25]
For any undirected connected graph G, the set V of vertices of G can be turned into a metric space by defining the distance between vertices x and y to be the length of the shortest edge path connecting them. This is also called shortest-path distance or geodesic distance. In geometric group theory this construction is applied to the Cayley graph of a (typically infinite) finitely-generated group, yielding the word metric. Up to a bilipschitz homeomorphism, the word metric depends only on the group and not on the chosen finite generating set.[15]
Distances between mathematical objects edit
In modern mathematics, one often studies spaces whose points are themselves mathematical objects. A distance function on such a space generally aims to measure the dissimilarity between two objects. Here are some examples:
- Functions to a metric space. If X is any set and M is a metric space, then the set of all bounded functions (i.e. those functions whose image is a bounded subset of ) can be turned into a metric space by defining the distance between two bounded functions f and g to be This metric is called the uniform metric or supremum metric.[26] If M is complete, then this function space is complete as well; moreover, if X is also a topological space, then the subspace consisting of all bounded continuous functions from X to M is also complete. When X is a subspace of , this function space is known as a classical Wiener space.
- String metrics and edit distances. There are many ways of measuring distances between strings of characters, which may represent sentences in computational linguistics or code words in coding theory. Edit distances attempt to measure the number of changes necessary to get from one string to another. For example, the Hamming distance measures the minimal number of substitutions needed, while the Levenshtein distance measures the minimal number of deletions, insertions, and substitutions; both of these can be thought of as distances in an appropriate graph.
- Graph edit distance is a measure of dissimilarity between two graphs, defined as the minimal number of graph edit operations required to transform one graph into another.
- Wasserstein metrics measure the distance between two measures on the same metric space. The Wasserstein distance between two measures is, roughly speaking, the cost of transporting one to the other.
- The set of all m by n matrices over some field is a metric space with respect to the rank distance .
- The Helly metric in game theory measures the difference between strategies in a game.
Hausdorff and Gromov–Hausdorff distance edit
The idea of spaces of mathematical objects can also be applied to subsets of a metric space, as well as metric spaces themselves. Hausdorff and Gromov–Hausdorff distance define metrics on the set of compact subsets of a metric space and the set of compact metric spaces, respectively.
Suppose (M, d) is a metric space, and let S be a subset of M. The distance from S to a point x of M is, informally, the distance from x to the closest point of S. However, since there may not be a single closest point, it is defined via an infimum:
Given two subsets S and T of M, their Hausdorff distance is
The Gromov–Hausdorff metric defines a distance between (isometry classes of) compact metric spaces. The Gromov–Hausdorff distance between compact spaces X and Y is the infimum of the Hausdorff distance over all metric spaces Z that contain X and Y as subspaces. While the exact value of the Gromov–Hausdorff distance is rarely useful to know, the resulting topology has found many applications.
Miscellaneous examples edit
- Given a metric space (X, d) and an increasing concave function such that f(t) = 0 if and only if t = 0, then is also a metric on X. If f(t) = tα for some real number α < 1, such a metric is known as a snowflake of d.[27]
- The tight span of a metric space is another metric space which can be thought of as an abstract version of the convex hull.
- The knight's move metric, the minimal number of knight's moves to reach one point in from another, is a metric on .
- The British Rail metric (also called the "post office metric" or the "SNCF metric") on a normed vector space is given by for distinct points and , and . More generally can be replaced with a function taking an arbitrary set to non-negative reals and taking the value at most once: then the metric is defined on by for distinct points and , and . The name alludes to the tendency of railway journeys to proceed via London (or Paris) irrespective of their final destination.
- The Robinson–Foulds metric used for calculating the distances between Phylogenetic trees in Phylogenetics[28]
Constructions edit
Product metric spaces edit
If are metric spaces, and N is the Euclidean norm on , then is a metric space, where the product metric is defined by
Similarly, a metric on the topological product of countably many metric spaces can be obtained using the metric
The topological product of uncountably many metric spaces need not be metrizable. For example, an uncountable product of copies of is not first-countable and thus is not metrizable.
Quotient metric spaces edit
If M is a metric space with metric d, and is an equivalence relation on M, then we can endow the quotient set with a pseudometric. The distance between two equivalence classes and is defined as
The quotient metric is characterized by the following universal property. If is a metric (i.e. 1-Lipschitz) map between metric spaces satisfying f(x) = f(y) whenever , then the induced function , given by , is a metric map
The quotient metric does not always induce the quotient topology. For example, the topological quotient of the metric space identifying all points of the form is not metrizable since it is not first-countable, but the quotient metric is a well-defined metric on the same set which induces a coarser topology. Moreover, different metrics on the original topological space (a disjoint union of countably many intervals) lead to different topologies on the quotient.[30]
A topological space is sequential if and only if it is a (topological) quotient of a metric space.[31]
Generalizations of metric spaces edit
There are several notions of spaces which have less structure than a metric space, but more than a topological space.
- Uniform spaces are spaces in which distances are not defined, but uniform continuity is.
- Approach spaces are spaces in which point-to-set distances are defined, instead of point-to-point distances. They have particularly good properties from the point of view of category theory.
- Continuity spaces are a generalization of metric spaces and posets that can be used to unify the notions of metric spaces and domains.
There are also numerous ways of relaxing the axioms for a metric, giving rise to various notions of generalized metric spaces. These generalizations can also be combined. The terminology used to describe them is not completely standardized. Most notably, in functional analysis pseudometrics often come from seminorms on vector spaces, and so it is natural to call them "semimetrics". This conflicts with the use of the term in topology.
Extended metrics edit
Some authors define metrics so as to allow the distance function d to attain the value ∞, i.e. distances are non-negative numbers on the extended real number line.[4] Such a function is also called an extended metric or "∞-metric". Every extended metric can be replaced by a real-valued metric that is topologically equivalent. This can be done using a subadditive monotonically increasing bounded function which is zero at zero, e.g. or .
Metrics valued in structures other than the real numbers edit
The requirement that the metric take values in can be relaxed to consider metrics with values in other structures, including:
- Ordered fields, yielding the notion of a generalised metric.
- More general directed sets. In the absence of an addition operation, the triangle inequality does not make sense and is replaced with an ultrametric inequality. This leads to the notion of a generalized ultrametric.[32]
These generalizations still induce a uniform structure on the space.
Pseudometrics edit
A pseudometric on is a function which satisfies the axioms for a metric, except that instead of the second (identity of indiscernibles) only for all is required.[33] In other words, the axioms for a pseudometric are:
- .
In some contexts, pseudometrics are referred to as semimetrics[34] because of their relation to seminorms.
Quasimetrics edit
Occasionally, a quasimetric is defined as a function that satisfies all axioms for a metric with the possible exception of symmetry.[35] The name of this generalisation is not entirely standardized.[36]
Quasimetrics are common in real life. For example, given a set X of mountain villages, the typical walking times between elements of X form a quasimetric because travel uphill takes longer than travel downhill. Another example is the length of car rides in a city with one-way streets: here, a shortest path from point A to point B goes along a different set of streets than a shortest path from B to A and may have a different length.
A quasimetric on the reals can be defined by setting
Given a quasimetric on X, one can define an R-ball around x to be the set . As in the case of a metric, such balls form a basis for a topology on X, but this topology need not be metrizable. For example, the topology induced by the quasimetric on the reals described above is the (reversed) Sorgenfrey line.
Metametrics or partial metrics edit
In a metametric, all the axioms of a metric are satisfied except that the distance between identical points is not necessarily zero. In other words, the axioms for a metametric are:
Metametrics appear in the study of Gromov hyperbolic metric spaces and their boundaries. The visual metametric on such a space satisfies for points on the boundary, but otherwise is approximately the distance from to the boundary. Metametrics were first defined by Jussi Väisälä.[37] In other work, a function satisfying these axioms is called a partial metric[38][39] or a dislocated metric.[33]
Semimetrics edit
A semimetric on is a function that satisfies the first three axioms, but not necessarily the triangle inequality:
Some authors work with a weaker form of the triangle inequality, such as:
ρ-relaxed triangle inequality ρ-inframetric inequality
The ρ-inframetric inequality implies the ρ-relaxed triangle inequality (assuming the first axiom), and the ρ-relaxed triangle inequality implies the 2ρ-inframetric inequality. Semimetrics satisfying these equivalent conditions have sometimes been referred to as quasimetrics,[40] nearmetrics[41] or inframetrics.[42]
The ρ-inframetric inequalities were introduced to model round-trip delay times in the internet.[42] The triangle inequality implies the 2-inframetric inequality, and the ultrametric inequality is exactly the 1-inframetric inequality.
Premetrics edit
Relaxing the last three axioms leads to the notion of a premetric, i.e. a function satisfying the following conditions:
This is not a standard term. Sometimes it is used to refer to other generalizations of metrics such as pseudosemimetrics[43] or pseudometrics;[44] in translations of Russian books it sometimes appears as "prametric".[45] A premetric that satisfies symmetry, i.e. a pseudosemimetric, is also called a distance.[46]
Any premetric gives rise to a topology as follows. For a positive real , the -ball centered at a point is defined as
A set is called open if for any point in the set there is an -ball centered at which is contained in the set. Every premetric space is a topological space, and in fact a sequential space. In general, the -balls themselves need not be open sets with respect to this topology. As for metrics, the distance between two sets and , is defined as
This defines a premetric on the power set of a premetric space. If we start with a (pseudosemi-)metric space, we get a pseudosemimetric, i.e. a symmetric premetric. Any premetric gives rise to a preclosure operator as follows:
Pseudoquasimetrics edit
The prefixes pseudo-, quasi- and semi- can also be combined, e.g., a pseudoquasimetric (sometimes called hemimetric) relaxes both the indiscernibility axiom and the symmetry axiom and is simply a premetric satisfying the triangle inequality. For pseudoquasimetric spaces the open -balls form a basis of open sets. A very basic example of a pseudoquasimetric space is the set with the premetric given by and The associated topological space is the Sierpiński space.
Sets equipped with an extended pseudoquasimetric were studied by William Lawvere as "generalized metric spaces".[47] From a categorical point of view, the extended pseudometric spaces and the extended pseudoquasimetric spaces, along with their corresponding nonexpansive maps, are the best behaved of the metric space categories. One can take arbitrary products and coproducts and form quotient objects within the given category. If one drops "extended", one can only take finite products and coproducts. If one drops "pseudo", one cannot take quotients.
Lawvere also gave an alternate definition of such spaces as enriched categories. The ordered set can be seen as a category with one morphism if and none otherwise. Using + as the tensor product and 0 as the identity makes this category into a monoidal category . Every (extended pseudoquasi-)metric space can now be viewed as a category enriched over :
- The objects of the category are the points of M.
- For every pair of points x and y such that , there is a single morphism which is assigned the object of .
- The triangle inequality and the fact that for all points x derive from the properties of composition and identity in an enriched category.
- Since is a poset, all diagrams that are required for an enriched category commute automatically.
Metrics on multisets edit
The notion of a metric can be generalized from a distance between two elements to a number assigned to a multiset of elements. A multiset is a generalization of the notion of a set in which an element can occur more than once. Define the multiset union as follows: if an element x occurs m times in X and n times in Y then it occurs m + n times in U. A function d on the set of nonempty finite multisets of elements of a set M is a metric[48] if
- if all elements of X are equal and otherwise (positive definiteness)
- depends only on the (unordered) multiset X (symmetry)
- (triangle inequality)
By considering the cases of axioms 1 and 2 in which the multiset X has two elements and the case of axiom 3 in which the multisets X, Y, and Z have one element each, one recovers the usual axioms for a metric. That is, every multiset metric yields an ordinary metric when restricted to sets of two elements.
A simple example is the set of all nonempty finite multisets of integers with . More complex examples are information distance in multisets;[48] and normalized compression distance (NCD) in multisets.[49]
See also edit
- Acoustic metric – Tensor characterizing signal-carrying properties in a medium
- Complete metric – Metric geometry
- Diversity (mathematics) – Generalization of metric spaces
- Glossary of Riemannian and metric geometry – Mathematics glossary
- Hilbert's fourth problem – Construct all metric spaces where lines resemble those on a sphere
- Metric tree
- Minkowski distance – Mathematical metric in normed vector space
- Signed distance function – Distance from a point to the boundary of a set
- Similarity measure – Real-valued function that quantifies similarity between two objects
- Space (mathematics) – Mathematical set with some added structure
- Ultrametric space – Type of metric space
Notes edit
- ^ Balls with rational radius around a point x form a neighborhood basis for that point.
- ^ In the context of intervals in the real line, or more generally regions in Euclidean space, bounded sets are sometimes referred to as "finite intervals" or "finite regions". However, they do not typically have a finite number of elements, and while they all have finite volume, so do many unbounded sets. Therefore this terminology is imprecise.
- ^ This differs from usage in Riemannian geometry, where geodesics are only locally shortest paths. Some authors define geodesics in metric spaces in the same way.[18][19]
Citations edit
- ^ Čech 1969, p. 42.
- ^ Burago, Burago & Ivanov 2001.
- ^ Heinonen 2001.
- ^ a b Burago, Burago & Ivanov 2001, p. 1.
- ^ Gromov 2007, p. xv.
- ^ Gleason, Andrew (1991). Fundamentals of Abstract Analysis (1st ed.). Taylor & Francis. p. 223. doi:10.1201/9781315275444. ISBN 9781315275444. S2CID 62222843.
- ^ Fréchet, M. (December 1906). "Sur quelques points du calcul fonctionnel". Rendiconti del Circolo Matematico di Palermo. 22 (1): 1–72. doi:10.1007/BF03018603. S2CID 123251660.
- ^ Blumberg, Henry (1927). "Hausdorff's Grundzüge der Mengenlehre". Bulletin of the American Mathematical Society. 6: 778–781. doi:10.1090/S0002-9904-1920-03378-1.
- ^ Rudin 1976, p. 30.
- ^ E.g. Burago, Burago & Ivanov 2001, p. xiii:
... for most of the last century it was a common belief that "geometry of manifolds" basically boiled down to "analysis on manifolds". Geometric methods heavily relied on differential machinery, as can be guessed from the name "Differential geometry".
- ^ Rudin, Mary Ellen. A new proof that metric spaces are paracompact Archived 2016-04-12 at the Wayback Machine. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.
- ^ Burago, Burago & Ivanov 2001, p. 2.
- ^ Burago, Burago & Ivanov 2001, p. 2.
Some authors refer to any distance-preserving function as an isometry, e.g. Munkres 2000, p. 181. - ^ Gromov 2007, p. xvii.
- ^ a b c Margalit & Thomas 2017.
- ^ Narici & Beckenstein 2011, pp. 47–66.
- ^ Burago, Burago & Ivanov 2001, Definition 2.3.1.
- ^ Burago, Burago & Ivanov 2001, Definition 2.5.27.
- ^ Gromov 2007, Definition 1.9.
- ^ Burago, Burago & Ivanov 2001, p. 127.
- ^ Heinonen 2007, p. 191.
- ^ Gigli, Nicola (2018-10-18). "Lecture notes on differential calculus on RCD spaces". Publications of the Research Institute for Mathematical Sciences. 54 (4): 855–918. arXiv:1703.06829. doi:10.4171/PRIMS/54-4-4. S2CID 119129867.
- ^ Linial, Nathan (2003). "Finite metric-spaces—combinatorics, geometry and algorithms". Proceedings of the ICM, Beijing 2002. Vol. 3. pp. 573–586. arXiv:math/0304466.
- ^ Bourgain, J. (1985). "On lipschitz embedding of finite metric spaces in Hilbert space". Israel Journal of Mathematics. 52 (1–2): 46–52. doi:10.1007/BF02776078. S2CID 121649019.
- ^ Jiří Matoušek and Assaf Naor, ed. "Open problems on embeddings of finite metric spaces". Archived 2010-12-26 at the Wayback Machine.
- ^ Ó Searcóid 2006, p. 107.
- ^ Gottlieb, Lee-Ad; Solomon, Shay (2014-06-08). Light spanners for snowflake metrics. SOCG '14: Proceedings of the thirtieth annual symposium on Computational geometry. pp. 387–395. arXiv:1401.5014. doi:10.1145/2582112.2582140.
- ^ Robinson, D.F.; Foulds, L.R. (February 1981). "Comparison of phylogenetic trees". Mathematical Biosciences. 53 (1–2): 131–147. doi:10.1016/0025-5564(81)90043-2. S2CID 121156920.
- ^ Burago, Burago & Ivanov 2001, Definition 3.1.12.
- ^ See Burago, Burago & Ivanov 2001, Example 3.1.17, although in this book the quotient is incorrectly claimed to be homeomorphic to the topological quotient.
- ^ Goreham, Anthony. Sequential convergence in Topological Spaces Archived 2011-06-04 at the Wayback Machine. Honours' Dissertation, Queen's College, Oxford (April, 2001), p. 14
- ^ Hitzler & Seda 2016, Definition 4.3.1.
- ^ a b Hitzler & Seda 2016, Definition 4.2.1.
- ^ Burago, Burago & Ivanov 2001, Definition 1.1.4.
- ^ Steen & Seebach (1995); Smyth (1988)
- ^ Rolewicz (1987) calls them "semimetrics". That same term is also frequently used for two other generalizations of metrics.
- ^ Väisälä 2005.
- ^ "Partial metrics: welcome". www.dcs.warwick.ac.uk. Archived from the original on 2017-07-27. Retrieved 2018-05-02.
- ^ Bukatin, Michael; Kopperman, Ralph; Matthews, Steve; Pajoohesh, Homeira (2009-10-01). "Partial Metric Spaces" (PDF). American Mathematical Monthly. 116 (8): 708–718. doi:10.4169/193009709X460831. S2CID 13969183.
- ^ Xia 2009.
- ^ Xia 2008.
- ^ a b Fraigniaud, Lebhar & Viennot 2008.
- ^ Buldygin & Kozachenko 2000.
- ^ Helemskii 2006.
- ^ Arkhangel'skii & Pontryagin (1990); Aldrovandi & Pereira (2017)
- ^ Deza & Laurent 1997.
- ^ Lawvere (1973); Vickers (2005)
- ^ a b Vitányi 2011.
- ^ Cohen & Vitányi 2012.
References edit
- Aldrovandi, Ruben; Pereira, José Geraldo (2017), An Introduction to Geometrical Physics (2nd ed.), Hackensack, New Jersey: World Scientific, p. 20, ISBN 978-981-3146-81-5, MR 3561561
- Arkhangel'skii, A. V.; Pontryagin, L. S. (1990), General Topology I: Basic Concepts and Constructions Dimension Theory, Encyclopaedia of Mathematical Sciences, Springer, ISBN 3-540-18178-4
- Bryant, Victor (1985). Metric spaces: Iteration and application. Cambridge University Press. ISBN 0-521-31897-1.
- Buldygin, V. V.; Kozachenko, Yu. V. (2000), Metric Characterization of Random Variables and Random Processes, Translations of Mathematical Monographs, vol. 188, Providence, Rhode Island: American Mathematical Society, p. 129, doi:10.1090/mmono/188, ISBN 0-8218-0533-9, MR 1743716
- Burago, Dmitri; Burago, Yuri; Ivanov, Sergei (2001). A course in metric geometry. Providence, RI: American Mathematical Society. ISBN 0-8218-2129-6.
- Čech, Eduard (1969). Point Sets. Academic Press. ISBN 0121648508.
- Cohen, Andrew R.; Vitányi, Paul M. B. (2012), "Normalized compression distance of multisets with applications", IEEE Transactions on Pattern Analysis and Machine Intelligence, 37 (8): 1602–1614, arXiv:1212.5711, doi:10.1109/TPAMI.2014.2375175, PMC 4566858, PMID 26352998
- Deza, Michel Marie; Laurent, Monique (1997), Geometry of Cuts and Metrics, Algorithms and Combinatorics, vol. 15, Springer-Verlag, Berlin, p. 27, doi:10.1007/978-3-642-04295-9, ISBN 3-540-61611-X, MR 1460488
- Fraigniaud, P.; Lebhar, E.; Viennot, L. (2008), "The inframetric model for the internet", 2008 IEEE INFOCOM - The 27th Conference on Computer Communications, pp. 1085–1093, CiteSeerX 10.1.1.113.6748, doi:10.1109/INFOCOM.2008.163, ISBN 978-1-4244-2026-1, S2CID 5733968
- Gromov, Mikhael (2007). Metric structures for Riemannian and non-Riemannian spaces. Boston: Birkhäuser. ISBN 978-0-8176-4582-3.
- Heinonen, Juha (2001). Lectures on analysis on metric spaces. New York: Springer. ISBN 0-387-95104-0.
- Heinonen, Juha (2007-01-24). "Nonsmooth calculus". Bulletin of the American Mathematical Society. 44 (2): 163–232. doi:10.1090/S0273-0979-07-01140-8.
- Helemskii, A. Ya. (2006), Lectures and Exercises on Functional Analysis, Translations of Mathematical Monographs, vol. 233, Providence, Rhode Island: American Mathematical Society, p. 14, doi:10.1090/mmono/233, ISBN 978-0-8218-4098-6, MR 2248303
- Hitzler, Pascal; Seda, Anthony (2016-04-19). Mathematical Aspects of Logic Programming Semantics. CRC Press. ISBN 978-1-4398-2962-2.
- Lawvere, F. William (December 1973). "Metric spaces, generalized logic, and closed categories". Rendiconti del Seminario Matematico e Fisico di Milano. 43 (1): 135–166. doi:10.1007/BF02924844. S2CID 1845177.
- Margalit, Dan; Thomas, Anne (2017). "Office Hour 7. Quasi-isometries". Office hours with a geometric group theorist. Princeton University Press. pp. 125–145. ISBN 978-1-4008-8539-8. JSTOR j.ctt1vwmg8g.11.
- Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Narici, Lawrence; Beckenstein, Edward (2011), Topological Vector Spaces, Pure and applied mathematics (Second ed.), Boca Raton, FL: CRC Press, ISBN 978-1584888666, OCLC 144216834
- Ó Searcóid, Mícheál (2006). Metric spaces. London: Springer. ISBN 1-84628-369-8.
- Papadopoulos, Athanase (2014). Metric spaces, convexity, and non-positive curvature (Second ed.). Zürich, Switzerland: European Mathematical Society. ISBN 978-3-03719-132-3.
- Rolewicz, Stefan (1987). Functional Analysis and Control Theory: Linear Systems. Springer. ISBN 90-277-2186-6.
- Rudin, Walter (1976). Principles of Mathematical Analysis (Third ed.). New York: McGraw-Hill. ISBN 0-07-054235-X. OCLC 1502474.
- Smyth, M. (1988), "Quasi uniformities: reconciling domains with metric spaces", in Main, M.; Melton, A.; Mislove, M.; Schmidt, D. (eds.), Mathematical Foundations of Programming Language Semantics, Lecture Notes in Computer Science, vol. 298, Springer-Verlag, pp. 236–253, doi:10.1007/3-540-19020-1_12, ISBN 978-3-540-19020-2
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology. Dover. ISBN 978-0-486-68735-3. MR 0507446.
- Vitányi, Paul M. B. (2011). "Information distance in multiples". IEEE Transactions on Information Theory. 57 (4): 2451–2456. arXiv:0905.3347. doi:10.1109/TIT.2011.2110130. S2CID 6302496.
- Väisälä, Jussi (2005). "Gromov hyperbolic spaces" (PDF). Expositiones Mathematicae. 23 (3): 187–231. doi:10.1016/j.exmath.2005.01.010. MR 2164775.
- Vickers, Steven (2005). "Localic completion of generalized metric spaces, I". Theory and Applications of Categories. 14 (15): 328–356. MR 2182680.
- Weisstein, Eric W. "Product Metric". MathWorld.
- Xia, Qinglan (2008). "The geodesic problem in nearmetric spaces". Journal of Geometric Analysis. 19 (2): 452–479. arXiv:0807.3377. doi:10.1007/s12220-008-9065-4. S2CID 17475581.
- Xia, Q. (2009). "The geodesic problem in quasimetric spaces". Journal of Geometric Analysis. 19 (2): 452–479. arXiv:0807.3377. doi:10.1007/s12220-008-9065-4. S2CID 17475581.
