This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
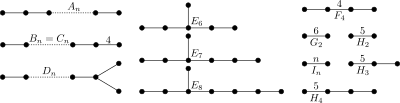

In geometry, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing a Coxeter group or sometimes a uniform polytope or uniform tiling constructed from the group.
A class of closely related objects is the Dynkin diagrams, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.[1]
Description
editA Coxeter group is a group that admits a presentation: where the mi,j are the elements of some symmetric matrix M which has 1s on its diagonal.[a] This matrix M, the Coxeter matrix, completely determines the Coxeter group.
Since the Coxeter matrix is symmetric, it can be viewed as the adjacency matrix of an edge-labeled graph that has vertices corresponding to the generators ri, and edges labeled with mi,j between the vertices corresponding to ri and rj. In order to simplify these diagrams, two changes can be made:
- Edges that are labeled with 2 can be omitted, with the missing edges being implied to be 2s. A label 2 indicates that the corresponding two generators commute; 2 is the smallest number that can be used to label an edge.
- Edges labeled 3 can be left unlabeled, with the implication that an unlabeled edge acts as a 3.
The resulting graph is a Coxeter-Dynkin diagram that describes the considered Coxeter group.
Schläfli matrix
editEvery Coxeter diagram has a corresponding Schläfli matrix (so named after Ludwig Schläfli), A, with matrix elements ai,j = aj,i = −2 cos(π/pi,j) where pi,j is the branch order between mirrors i and j; that is, π/pi,j is the dihedral angle between mirrors i and j. As a matrix of cosines, A is also called a Gramian matrix. All Coxeter group Schläfli matrices are symmetric because their root vectors are normalized. A is closely related to the Cartan matrix, used in the similar but directed graph: the Dynkin diagram, in the limited cases of p = 2,3,4, and 6, which are generally not symmetric.
The determinant of the Schläfli matrix is called the Schläflian;[citation needed] the Schläflian and its sign determine whether the group is finite (positive), affine (zero), or indefinite (negative).[2] This rule is called Schläfli's Criterion.[3][failed verification]
The eigenvalues of the Schläfli matrix determine whether a Coxeter group is of finite type (all positive), affine type (all non-negative, at least one is zero), or indefinite type (otherwise). The indefinite type is sometimes further subdivided, e.g. into hyperbolic and other Coxeter groups. However, there are multiple non-equivalent definitions for hyperbolic Coxeter groups. We use the following definitions:
- A Coxeter group with connected diagram is hyperbolic if it is neither of finite nor affine type, but every proper connected subdiagram is of finite or affine type.
- A hyperbolic Coxeter group is compact if all its subgroups are finite (i.e. have positive determinants), and paracompact if all its subgroups are finite or affine (i.e. have nonnegative determinants).
Finite and affine groups are also called elliptical and parabolic respectively. Hyperbolic groups are also called Lannér, after F. Lannér who enumerated the compact hyperbolic groups in 1950,[4] and Koszul (or quasi-Lannér) for the paracompact groups.
Rank 2 Coxeter groups
editThe type of a rank 2 Coxeter group, i.e. generated by two different mirrors, is fully determined by the determinant of the Schläfli matrix, as this determinant is simply the product of the eigenvalues: finite (positive determinant), affine (zero determinant), or hyperbolic (negative determinant) type. Coxeter uses an equivalent bracket notation which lists sequences of branch orders as a substitute for the node-branch graphic diagrams. Rational solutions [p/q], ![]()
![]()
![]()
![]()
![]() , also exist, with gcd(p,q) = 1; these define overlapping fundamental domains. For example, 3/2, 4/3, 5/2, 5/3, 5/4, and 6/5.
, also exist, with gcd(p,q) = 1; these define overlapping fundamental domains. For example, 3/2, 4/3, 5/2, 5/3, 5/4, and 6/5.
| Type | Finite | Affine | Hyperbolic | |||||
|---|---|---|---|---|---|---|---|---|
| Geometry | 
|

|

|

|
... | 
|

|

|
| Coxeter diagram Bracket notation |
[ ] |
[2] |
[3] |
[4] |
[p] |
[∞] |
[∞] |
[iπ/λ] |
| Order | 2 | 4 | 6 | 8 | 2p | ∞ | ||
| Mirror lines are colored to correspond to Coxeter diagram nodes. Fundamental domains are alternately colored. | ||||||||
| Rank 2 Coxeter group diagrams | |||||||
|---|---|---|---|---|---|---|---|
| Order p |
Group | Coxeter diagram | Schläfli matrix | ||||
| Determinant | |||||||
| Finite (Determinant > 0) | |||||||
| 2 | I2(2) = A1×A1 | [2] | 4 | ||||
| 3 | I2(3) = A2 | [3] | 3 | ||||
| 3/2 | [3/2] | ||||||
| 4 | I2(4) = B2 | [4] | 2 | ||||
| 4/3 | [4/3] | ||||||
| 5 | I2(5) = H2 | [5] | ≈ 1.38196601125 | ||||
| 5/4 | [5/4] | ||||||
| 5/2 | [5/2] | ≈ 3.61803398875 | |||||
| 5/3 | [5/3] | ||||||
| 6 | I2(6) = G2 | [6] | 1 | ||||
| 6/5 | [6/5] | ||||||
| 8 | I2(8) | [8] | ≈ 0.58578643763 | ||||
| 10 | I2(10) | [10] | ≈ 0.38196601125 | ||||
| 12 | I2(12) | [12] | ≈ 0.26794919243 | ||||
| p | I2(p) | [p] | |||||
| Affine (Determinant = 0) | |||||||
| ∞ | I2(∞) = = | [∞] | 0 | ||||
| Hyperbolic (Determinant ≤ 0) | |||||||
| ∞ | [∞] | 0 | |||||
| ∞ | [iπ/λ] | ||||||
Geometric visualizations
editThe Coxeter–Dynkin diagram can be seen as a graphic description of the fundamental domain of mirrors. A mirror represents a hyperplane within a spherical, Euclidean, or hyperbolic space of given dimension. (In 2D spaces, a mirror is a line; in 3D, a mirror is a plane.)
These visualizations show the fundamental domains for 2D and 3D Euclidean groups, and for 2D spherical groups. For each, the Coxeter diagram can be deduced by identifying the hyperplane mirrors and labelling their connectivity, ignoring 90-degree dihedral angles (order 2; see footnote [a] below).
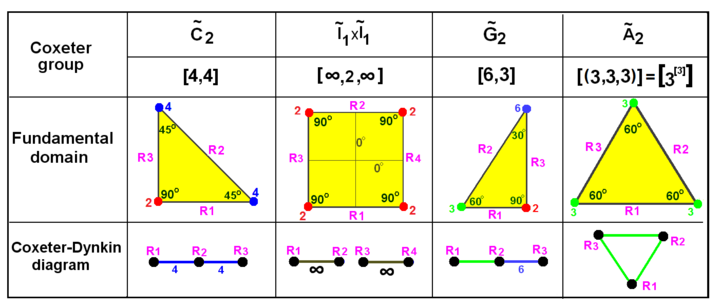 Coxeter groups in the Euclidean plane with equivalent diagrams. Here, domain vertices are labeled as graph branches 1, 2, etc., and are colored by their reflection order (connectivity). Reflections are labeled as graph nodes R1, R2, etc. Reflections at 90 degrees are inactive in the sense that, together, they generate no new reflections;[b] they are therefore not connected to each other by a branch on the diagram. Parallel mirrors are connected to each other by an ∞ labeled branch. The square of the prismatic group × is shown as a doubling of the triangle around its R2 side*, but can also be created as a rectangular domain from doubling the triangle around its R2 side*. The triangle is a doubling of the triangle around its R3 side*. | |
 Many Coxeter groups in the hyperbolic plane can be extended from the Euclidean cases as a series of hyperbolic solutions. | |
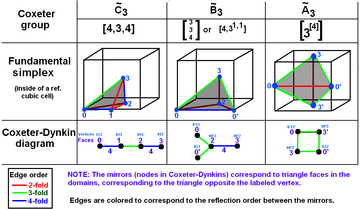 Coxeter groups in 3-space with diagrams. Mirrors (triangle faces) are labeled by opposite vertex: 0, ..., 3. Branches are colored by their reflection order. fills 1/48 of the cube. fills 1/24 of the cube. fills 1/12 of the cube. |
 Coxeter groups in the sphere with equivalent diagrams. One fundamental domain is outlined in yellow. Domain vertices (and graph branches) are colored by their reflection order. |
Application to uniform polytopes
edit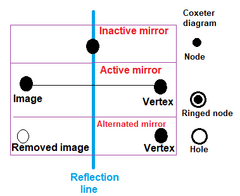 In constructing uniform polytopes, nodes are marked as active by a ring if a generator point is off the mirror, creating a new edge between a generator point and its mirror image. An unringed node represents an inactive mirror that generates no new points. A ring with no node is called a hole. |
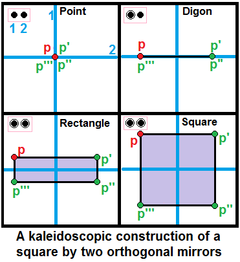 Two orthogonal mirrors can be used to generate a square, |
Coxeter–Dynkin diagrams can explicitly enumerate nearly all classes of uniform polytope and uniform tessellations. Every uniform polytope with pure reflective symmetry (all but a few special cases have pure reflectional symmetry) can be represented by a Coxeter–Dynkin diagram with permutations of markups. Each uniform polytope can be generated using such mirrors and a single generator point: mirror images create new points as reflections, then polytope edges can be defined between points and a mirror image point. Faces are generated by the repeated reflection of an edge eventually wrapping around to the original generator; the final shape, as well as any higher-dimensional facets, are likewise created by the face being reflected to enclose an area.
To specify the generating vertex, one or more nodes are marked with rings, meaning that the vertex is not on the mirror(s) represented by the ringed node(s). (If two or more mirrors are marked, the vertex is equidistant from them.) A mirror is active (creates reflections) only with respect to points not on it. A diagram needs at least one active node to represent a polytope. An unconnected diagram (subgroups separated by order-2 branches, or orthogonal mirrors) requires at least one active node in each subgraph.
All regular polytopes, represented by Schläfli symbol {p, q, r, ...}, can have their fundamental domains represented by a set of n mirrors with a related Coxeter–Dynkin diagram of a line of nodes and branches labeled by p, q, r, ..., with the first node ringed.
Uniform polytopes with one ring correspond to generator points at the corners of the fundamental domain simplex. Two rings correspond to the edges of simplex and have a degree of freedom, with only the midpoint as the uniform solution for equal edge lengths. In general k-ring generator points are on (k-1)-faces of the simplex, and if all the nodes are ringed, the generator point is in the interior of the simplex.
The special case of uniform polytopes with non-reflectional symmetry is represented by a secondary markup where the central dot of a ringed node is removed (called a hole). These shapes are alternations of polytopes with reflective symmetry, implying that every other vertex is deleted. The resulting polytope will have a subsymmetry of the original Coxeter group. A truncated alternation is called a snub.
- A single node represents a single mirror. This is called group A1. If ringed this creates a line segment perpendicular to the mirror, represented as {}.
- Two unattached nodes represent two perpendicular mirrors. If both nodes are ringed, a rectangle can be created, or a square if the point is at equal distance from both mirrors.
- Two nodes attached by an order-n branch can create an n-gon if the point is on one mirror, and a 2n-gon if the point is off both mirrors. This forms the I1(n) group.
- Two parallel mirrors can represent an infinite polygon I1(∞) group, also called Ĩ1.
- Three mirrors in a triangle form images seen in a traditional kaleidoscope and can be represented by three nodes connected in a triangle. Repeating examples will have branches labeled as (3 3 3), (2 4 4), (2 3 6), although the last two can be drawn as a line (with the 2 branches ignored). These will generate uniform tilings.
- Three mirrors can generate uniform polyhedra; including rational numbers gives the set of Schwarz triangles.
- Three mirrors with one perpendicular to the other two can form the uniform prisms.
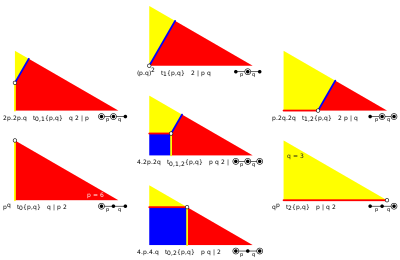 There are 7 reflective uniform constructions within a general triangle, based on 7 topological generator positions within the fundamental domain. Every active mirror generates an edge, with two active mirrors have generators on the domain sides and three active mirrors has the generator in the interior. One or two degrees of freedom can be solved for a unique position for equal edge lengths of the resulting polyhedron or tiling. |
 Example 7 generators on octahedral symmetry, fundamental domain triangle (4 3 2), with 8th snub generation as an alternation |
The duals of the uniform polytopes are sometimes marked up with a perpendicular slash replacing ringed nodes, and a slash-hole for hole nodes of the snubs. For example, ![]()
![]()
![]() represents a rectangle (as two active orthogonal mirrors), and
represents a rectangle (as two active orthogonal mirrors), and ![]()
![]()
![]() represents its dual polygon, the rhombus.
represents its dual polygon, the rhombus.
Examples with polyhedra and tilings
editFor example, the B3 Coxeter group has a diagram: ![]()
![]()
![]()
![]()
![]() . This is also called octahedral symmetry.
. This is also called octahedral symmetry.
There are 7 convex uniform polyhedra that can be constructed from this symmetry group and 3 from its alternation subsymmetries, each with a uniquely marked up Coxeter–Dynkin diagram. The Wythoff symbol represents a special case of the Coxeter diagram for rank 3 graphs, with all 3 branch orders named, rather than suppressing the order 2 branches. The Wythoff symbol is able to handle the snub form, but not general alternations without all nodes ringed.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
The same constructions can be made on disjointed (orthogonal) Coxeter groups like the uniform prisms, and can be seen more clearly as tilings of dihedrons and hosohedra on the sphere, like this [6]×[] or [6,2] family:
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||

|

|

|

|
|

|

| ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Duals to uniforms | ||||||||||||||

|

|

|

|

|

|

|

|

| ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
In comparison, the [6,3], ![]()
![]()
![]()
![]()
![]() family produces a parallel set of 7 uniform tilings of the Euclidean plane, and their dual tilings. There are again 3 alternations and some half symmetry version.
family produces a parallel set of 7 uniform tilings of the Euclidean plane, and their dual tilings. There are again 3 alternations and some half symmetry version.
| Uniform hexagonal/triangular tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,3], (*632) | [6,3]+ (632) |
[6,3+] (3*3) | |||||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | s{3,6} | |||

|

|

|

|

|

|

|

|

| |||
| 63 | 3.122 | (3.6)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Uniform duals | |||||||||||

|

|

|

|

|

|

|

|

| |||
| V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 | V36 | |||
In the hyperbolic plane [7,3], ![]()
![]()
![]()
![]()
![]() family produces a parallel set of uniform tilings, and their dual tilings. There is only 1 alternation (snub) since all branch orders are odd. Many other hyperbolic families of uniform tilings can be seen at uniform tilings in hyperbolic plane.
family produces a parallel set of uniform tilings, and their dual tilings. There is only 1 alternation (snub) since all branch orders are odd. Many other hyperbolic families of uniform tilings can be seen at uniform tilings in hyperbolic plane.
| Uniform heptagonal/triangular tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,3], (*732) | [7,3]+, (732) | ||||||||||

|

|

|

|

|

|

|

| ||||
| {7,3} | t{7,3} | r{7,3} | t{3,7} | {3,7} | rr{7,3} | tr{7,3} | sr{7,3} | ||||
| Uniform duals | |||||||||||

|

|

|

|

|

|

|

| ||||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Very-extended Coxeter diagrams
editOne usage includes a very-extended definition from the direct Dynkin diagram usage which considers affine groups as extended, hyperbolic groups over-extended, and a third node as very-extended simple groups. These extensions are usually marked by an exponent of 1,2, or 3 + symbols for the number of extended nodes. This extending series can be extended backwards, by sequentially removing the nodes from the same position in the graph, although the process stops after removing branching node. The E8 extended family is the most commonly shown example extending backwards from E3 and forwards to E11.
The extending process can define a limited series of Coxeter graphs that progress from finite to affine to hyperbolic to Lorentzian. The determinant of the Cartan matrices determine where the series changes from finite (positive) to affine (zero) to hyperbolic (negative), and ending as a Lorentzian group, containing at least one hyperbolic subgroup.[5] The noncrystallographic Hn groups forms an extended series where H4 is extended as a compact hyperbolic and over-extended into a lorentzian group.
The determinant of the Schläfli matrix by rank are:[6]
- det(A1n = [2n−1]) = 2n (Finite for all n)
- det(An = [3n−1]) = n + 1 (finite for all n)
- det(Bn = [4,3n−2]) = 2 (finite for all n)
- det(Dn = [3n−3,1,1]) = 4 (finite for all n)
Determinants of the Schläfli matrix in exceptional series are:
- det(En = [3n−3,2,1]) = 9 − n (finite for E3 (= A2A1), E4 (= A4), E5 (= D5), E6, E7 and E8, affine at E9 (), hyperbolic at E10)
- det([3n−4,3,1]) = 2(8 − n) (finite for n = 4 to 7, affine (), and hyperbolic at n = 8.)
- det([3n−4,2,2]) = 3(7 − n) (finite for n = 4 to 6, affine (), and hyperbolic at n = 7.)
- det(Fn = [3,4,3n−3]) = 5 − n (finite for F3 (= B3) to F4, affine at F5 (), hyperbolic at F6)
- det(Gn = [6,3n−2]) = 3 − n (finite for G2, affine at G3 (), hyperbolic at G4)
| Finite | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank n | [3[7],3n−7] | [4,33,3n−6,1] | [31,1,3,3,3n−6,1] | [3n−5,2,2] | [3[8],3n−8] | [4,34,3n−7,1] | [31,1,3,3,3,3n−7,1] | [3n−5,3,1] | En=[3n−4,2,1] |
| 3 | [3−1,2,1] E3=A2A1 | ||||||||
| 4 | [3−1,2,2] A22 |
[3−1,3,1] A3A1 |
[30,2,1] E4=A4 | ||||||
| 5 | [4,3,3,3,3−1,1] B4A1 |
[31,1,3,3,3−1,1] D4A1 |
[30,2,2] A5 |
[30,3,1] A5 |
[31,2,1] E5=D5 | ||||
| 6 | [35] A6 |
[4,34] B6 |
[31,1,3,3,3] D6 |
[31,2,2] E6 |
[4,3,3,3,3,3−1,1] B5A1 |
[31,1,3,3,3,3−1,1] D5A1 |
[31,3,1] D6 |
[32,2,1] E6 * | |
| 7 | [3[7]] |
[4,33,31,1] |
[31,1,3,3,31,1] |
[32,2,2] |
[36] A7 |
[4,35] B7 |
[31,1,3,3,3,30,1] D7 |
[32,3,1] E7 * |
[33,2,1] E7 * |
| 8 | [3[7],3] |
[4,33,32,1] |
[31,1,3,3,32,1] |
[33,2,2] |
[3[8]] * |
[4,34,31,1] * |
[31,1,3,3,3,31,1] * |
[33,3,1] * |
[34,2,1] E8 * |
| 9 | [3[7],3,3] A6+++ |
[4,33,33,1] B6+++ |
[31,1,3,3,33,1] D6+++ |
[34,2,2] E6+++ |
[3[8],3] * |
[4,34,32,1] * |
[31,1,3,3,3,32,1] * |
[34,3,1] * |
[35,2,1] E9= * |
| 10 | [3[8],3,3] A7+++ * |
[4,34,33,1] B7+++ * |
[31,1,3,3,3,33,1] D7+++ * |
[35,3,1] E7+++ * |
[36,2,1] E10= * | ||||
| 11 | [37,2,1] E11=E8+++ * | ||||||||
| Det(Mn) | 7(7−n) | 2(7−n) | 4(7−n) | 3(7−n) | 8(8−n) | 2(8−n) | 4(8−n) | 2(8−n) | 9−n |
Geometric folding
edit| φA : AΓ → AΓ' for finite types | |||
|---|---|---|---|
| Γ | Γ' | Folding description | Coxeter–Dynkin diagrams |
| I2(h) | Γ(h) | Dihedral folding | 
|
| Bn | A2n | (I,sn) | |
| Dn+1, A2n-1 | (A3,±ε) | ||
| F4 | E6 | (A3,±ε) | |
| H4 | E8 | (A4,±ε) | |
| H3 | D6 | ||
| H2 | A4 | ||
| G2 | A5 | (A5,±ε) | |
| D4 | (D4,±ε) | ||
| φ: AΓ+ → AΓ'+ for affine types | |||
| Locally trivial | 
| ||
| (I,sn) | |||
| , | (A3,±ε) | ||
| , | (A3,±ε) | ||
| (I,sn) | |||
| (I,sn) & (I,s0) | |||
| (A3,ε) & (I,s0) | |||
| (A3,ε) & (A3,ε') | |||
| (A3,−ε) & (A3,−ε') | |||
| (I,s1) | |||
| , | (A3,±ε) | ||
| , | (A5,±ε) | ||
| , | (B3,±ε) | ||
| , | (D4,±ε) | ||
A (simply-laced) Coxeter–Dynkin diagram (finite, affine, or hyperbolic) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called "folding".[8][9]
For example, in D4 folding to G2, the edge in G2 points from the class of the 3 outer nodes (valence 1), to the class of the central node (valence 3). And E8 folds into 2 copies of H4, the second copy scaled by τ.[10]
Geometrically this corresponds to orthogonal projections of uniform polytopes and tessellations. Notably, any finite simply-laced Coxeter–Dynkin diagram can be folded to I2(h), where h is the Coxeter number, which corresponds geometrically to a projection to the Coxeter plane.
 A few hyperbolic foldings |
Complex reflections
editCoxeter–Dynkin diagrams have been extended to complex space, Cn where nodes are unitary reflections of period greater than 2. Nodes are labeled by an index, assumed to be 2 for ordinary real reflection if suppressed. Coxeter writes the complex group, p[q]r, as diagram ![]()
![]()
![]()
![]()
![]() .[11]
.[11]
A 1-dimensional regular complex polytope in is represented as ![]() , having p vertices. Its real representation is a regular polygon, {p}. Its symmetry is p[] or
, having p vertices. Its real representation is a regular polygon, {p}. Its symmetry is p[] or ![]() , order p. A unitary operator generator for
, order p. A unitary operator generator for ![]() is seen as a rotation in by 2π/p radians counter clockwise, and a
is seen as a rotation in by 2π/p radians counter clockwise, and a ![]() edge is created by sequential applications of a single unitary reflection. A unitary reflection generator for a 1-polytope with p vertices is e2πi/p = cos(2π/p) + i sin(2π/p). When p = 2, the generator is eπi = –1, the same as a point reflection in the real plane.
edge is created by sequential applications of a single unitary reflection. A unitary reflection generator for a 1-polytope with p vertices is e2πi/p = cos(2π/p) + i sin(2π/p). When p = 2, the generator is eπi = –1, the same as a point reflection in the real plane.
In a higher polytope, p{} or ![]() represents a p-edge element, with a 2-edge, {} or
represents a p-edge element, with a 2-edge, {} or ![]() , representing an ordinary real edge between two vertices.
, representing an ordinary real edge between two vertices.
 Complex 1-polytopes, |
 12 irreducible Shephard groups with their subgroup index relations.[12] Subgroups index 2 relate by removing a real reflection: p[2q]2 → p[q]p, index 2. p[4]q → p[q]p, index q. |
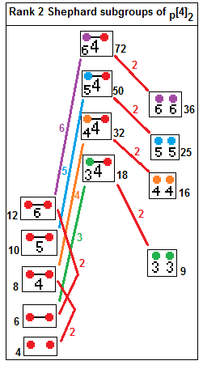 p[4]2 subgroups: p=2,3,4... p[4]2 → [p], index p p[4]2 → p[]×p[], index 2 |
A regular complex polygon in , has the form p{q}r or Coxeter diagram ![]()
![]()
![]()
![]()
![]() . The symmetry group of a regular complex polygon
. The symmetry group of a regular complex polygon ![]()
![]()
![]()
![]()
![]() is not called a Coxeter group, but instead a Shephard group, a type of Complex reflection group. The order of p[q]r is .[13]
is not called a Coxeter group, but instead a Shephard group, a type of Complex reflection group. The order of p[q]r is .[13]
The rank 2 Shephard groups are: 2[q]2, p[4]2, 3[3]3, 3[6]2, 3[4]3, 4[3]4, 3[8]2, 4[6]2, 4[4]3, 3[5]3, 5[3]5, 3[10]2, 5[6]2, and 5[4]3 or ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() of order 2q, 2p2, 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, and 1800 respectively.
of order 2q, 2p2, 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, and 1800 respectively.
The symmetry group p1[q]p2 is represented by 2 generators R1, R2, where:
- R1p1 = R2p2 = I.
If q is even, (R2R1)q/2 = (R1R2)q/2. If q is odd, (R2R1)(q-1)/2R2 = (R1R2)(q-1)/2R1. When q is odd, p1=p2.
The group ![]()
![]()
![]() or [1 1 1]p is defined by 3 period 2 unitary reflections {R1, R2, R3}:
or [1 1 1]p is defined by 3 period 2 unitary reflections {R1, R2, R3}:
- R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R1)p = 1.
The period p can be seen as a double rotation in real .
A similar group ![]()
![]()
![]() or [1 1 1](p) is defined by 3 period 2 unitary reflections {R1, R2, R3}:
or [1 1 1](p) is defined by 3 period 2 unitary reflections {R1, R2, R3}:
- R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R2)p = 1.
See also
edit- Coxeter group
- Schwarz triangle
- Goursat tetrahedron
- Dynkin diagram
- Uniform polytope
- Wythoff construction and Wythoff symbol
References
edit- ^ Hall, Brian C. (2003), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 978-0-387-40122-5
- ^ Borovik, Alexandre; Borovik, Anna (2010). Mirrors and reflections. Springer. pp. 118–119.
- ^ Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, sec. 7.7, p. 133, Schläfli's Criterion
- ^ Lannér F., On complexes with transitive groups of automorphisms, Medd. Lunds Univ. Mat. Sem. [Comm. Sem. Math. Univ. Lund], 11 (1950), 1–71
- ^ De Buyl, Sophie (2006). "Kac-Moody Algebras in M-theory". arXiv:hep-th/0608161.
- ^ Cartan–Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982
- ^ John Crisp, 'Injective maps between Artin groups', in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Archived 2005-10-16 at the Wayback Machine, pp. 13-14, and googlebook, Geometric group theory down under, p. 131
- ^ Zuber, Jean-Bernard (1998). "Generalized Dynkin diagrams and root systems and their folding". Topological Field Theory: 28–30. arXiv:hep-th/9707046. Bibcode:1998tftp.conf..453Z. CiteSeerX 10.1.1.54.3122.
- ^ Dechant, Pierre-Philippe; Boehm, Celine; Twarock, Reidun (2013). "Affine extensions of non-crystallographic Coxeter groups induced by projection". Journal of Mathematical Physics. 54 (9): 093508. arXiv:1110.5228. Bibcode:2013JMP....54i3508D. doi:10.1063/1.4820441. S2CID 59469917.
- ^ Dechant, Pierre-Philippe (2017). "The E 8 Geometry from a Clifford Perspective". Advances in Applied Clifford Algebras. 27: 397–421. doi:10.1007/s00006-016-0675-9.
- ^ Coxeter, Complex Regular Polytopes, second edition, (1991)
- ^ Coxeter, Complex Regular Polytopes, p. 177, Table III
- ^ Unitary Reflection Groups, p.87
Further reading
edit- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1], Googlebooks [2]
- (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Coxeter, Regular Polytopes (1963), Macmillan Company
- Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
- H.S.M. Coxeter and W. O. J. Moser, Generators and Relations for Discrete Groups 4th ed, Springer-Verlag, New York, 1980
- Norman Johnson, Geometries and Transformations, Chapters 11,12,13, preprint 2011
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups, 1999, Volume 4, Issue 4, pp. 329–353 [3] [4]
- Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups Archived 2023-03-26 at the Wayback Machine PDF Can. J. Math. Vol. 51 (6), 1999, pp. 1307–1336
External links
edit- Weisstein, Eric W. "Coxeter–Dynkin diagram". MathWorld.
- October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library.

![{\displaystyle \left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)

![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92222bfe2eeefe46dddcc56620241d8efd5ef1)
![{\displaystyle \left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db286eb5ca733d2b6ab1c5f194f03593440b5b3a)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dcf61f3b1fac33acafec6ac2d577c66f9f69306)
![{\displaystyle \left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a16582176db9cb488aa850d0b0a970ff0a62cd6)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8548776ee20b1e4a17df57227d372025e5bcbd65)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51483cac6134b485a8a8ea0d9e2fee62fda6d13a)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {2}}}}\\-{\sqrt {2+{\sqrt {2}}}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76feec8c86bbfeb5ce6439e1293efa582074902f)

![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cae955a07738bbf5a75ab02e8a5f2597346acaa)

![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f97b80af547d6ad0bcd4cc495671b2f7535d98)

![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71dd5a3c2a3aa08ab89d00e05a0afe4db4876ff8)



![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\cosh(2\lambda )\\-2\cosh(2\lambda )&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7051e92a35badbc10b3096bd2e43a4e328f19674)













































































































