In supramolecular chemistry,[1] host–guest chemistry describes complexes that are composed of two or more molecules or ions that are held together in unique structural relationships by forces other than those of full covalent bonds. Host–guest chemistry encompasses the idea of molecular recognition and interactions through non-covalent bonding. Non-covalent bonding is critical in maintaining the 3D structure of large molecules, such as proteins and is involved in many biological processes in which large molecules bind specifically but transiently to one another.
Although non-covalent interactions could be roughly divided into those with more electrostatic or dispersive contributions, there are few commonly mentioned types of non-covalent interactions: ionic bonding, hydrogen bonding, van der Waals forces and hydrophobic interactions.[2]
Host-guest interaction has raised dramatical attention since it was discovered. It is an important field, because many biological processes require the host-guest interaction, and it can be useful in some material designs. There are several typical host molecules, such as, cyclodextrin, crown ether, et al.
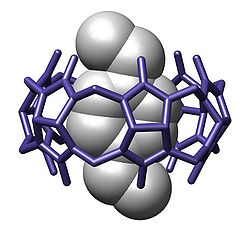

Overview edit
Although van der Waals postulated the intermolecular interaction in 1873, in 1894, Fischer built a philosophical root for supramolecular chemistry. He pointed out that enzyme-protein interactions behave in a "lock-and-key" manner. This interaction is the foundation to host-guest chemistry. With the deeper understanding of the non-covalent interactions, for example, the clear elucidation of DNA structure, chemists started to emphasize the importance of non-covalent interactions.[5] In 1967, Charles J. Pedersen discovered crown ethers, which are ring-like structures capable of chelating certain metal ions. Then, in 1969, Jean-Marie Lehn discovered a class of molecules similar to crown ethers, called cryptands. After that, Donald J. Cram synthesized many variations to crown ethers, on top of separate molecules capable of selective interaction with certain chemicals. The three scientists were awarded the Nobel Prize in Chemistry in 1987 for "development and use of molecules with structure-specific interactions of high selectivity”.[6] In 2016, Bernard L. Feringa, Sir J. Fraser Stoddart, and Jean-Pierre Sauvage were awarded the Nobel Prize in Chemistry, "for the design and synthesis of molecular machines".[7]
Supramolecular chemistry refers to the chemical systems that contains discrete number chemical components. The strengths of the systems vary from the intermolecular forces to covalent bindings. The researchers mentioned above created and enlarged the area of host-guest interaction, one of the most important concepts of the supramolecular chemistry fields. There are two significant components in the host-guest interaction. One is the "host molecules", which usually have "pore-like" structure that is able to capture some other molecules. The other one is the "guest molecules", which are generally smaller than the host molecules, and capable of binding the host molecules. The driving forces of the interaction might vary in different cases, such as hydrophobic effect, chelate effect, van der Waals force, et al.[8] Different bindings will provide variant properties for the materials, i.e., stimuli-responsiveness, self-healing, matrix rigidification. As a consequence, the host-guest interaction can be applied for self-healing materials, stimuli-responsive materials, room-temperature phosphorescence (RTP), improvement of mechanical properties, et al. The sizes of the host and guest molecules play an essential role in the interactions, and some typical examples of the host interactions will be discussed as follows.[8][9][10][11]
Host–guest chemistry is a branch of supramolecular chemistry in which a host molecule binds a so-called guest molecule or ion. The two components of the complex interact by non-covalent forces, most commonly by hydrogen-bonding. Binding between host and guest can be highly selective, in which case the interaction is called molecular recognition. Often, a dynamic equilibrium exist between the unbound and the bound states:
- H ="host", G ="guest", HG ="host–guest complex"
The "host" component is often the larger molecule, and it encloses the smaller, "guest", molecule. In biological systems, the analogous terms of host and guest are commonly referred to as enzyme and substrate respectively.[12]
Main types of macrocyclic hosts edit
Crown ether edit
Crown ethers are ring-like structures composed of several units of ethylene glycol. Because the radius of their pores are similar to that of alkali metal ions, crown ethers are well known for their ability to bind metallic ions. For example, 12-crown-4, 15-crown-5, 18-crown-6, 21-crown-7, and 24-crown-8 interact with potassium, sodium, ammonium, and calcium ions, respectively.[8] Among the aforementioned crown ethers, all the ions have the strongest binding affinity with 18-crown-6 because the size of 18-crown-6 most closely matches that of the ions. Besides ionic species, crown ethers can also bind to neutral molecules, e.g., 1, 2, 3- triazole. Crown ethers can also be threaded with long, linear molecules and/or polymers, giving rise to supramolecular structures called rotaxanes. Given that the crown ethers are not bound to the chains, they can move up and down the threading molecule.[11]
Cyclodextrin edit
Cyclodextrin (CD) is composed of several glucose units and connects by ether bonds. There are three kinds of CDs, α-CD (6 units), β-CD (7 units), and γ-CD (8 units). The heights of the structure are all around 8 Å, while the cavity sizes of them are different, around 5, 6, and 8 Å, respectively. By comparing the size of the guest molecule and the CD, the binding behavior can be predicted. For instance, if the guest molecule is larger than the CD, it can be assumed that the binding will not occur. Typically, the α-CD can thread onto one PEG chain, while γ-CD can thread onto 2 PEG chains. β-CD can bind with thiophene-based molecule.[8]
Cryptophanes edit
The structure of cryptophanes contain 6 phenyl rings, mainly connected in 4 ways . Due to the phenyl groups and aliphatic chains, the cages inside cryptophanes are highly hydrophobic, suggesting the capability of capturing non-polar molecules. Based on this, cryptophanes can be employed to capture xenon in aqueous solution, which could be helpful in biological studies.[8]
Resorcinarenes and Pyrogallolarenes edit
One of the classic structures of resorcinarenes and pyrogallolarenes is shown below. Because of the phenol group, some hydrogen bonds are foromed among the molecules. Sometimes, the binding ratio of the host and guest could reach 2 : 1.[8]
Other receptors (cucurbit[n]urils, CB) edit
Cucurbit[n]urils have similar size of γ-CD, which also behave similarly (e.g., 1 cucurbit[n]uril can thread onto 2 PEG chains).[8]
Thermodynamic principles of host–guest interactions edit
The thermodynamics of the host and guest interaction can be assessed by NMR spectroscopy, UV/visible spectroscopy, and isothermal titration calorimetry.[13] Quantitative analysis of binding constant values provides useful thermodynamic information.[12]
An association constant, can be defined by the expression
where {HG} is the thermodynamic activity of the complex at equilibrium. {H} represents the activity of the host and {G} the activity of the guest. The quantities , and are the corresponding concentrations and is a quotient of activity coefficients.
In practice the equilibrium constant is usually defined in terms of concentrations.
When this definition is used, it is implied that the quotient of activity coefficients has a numerical value of one. It then appears that the equilibrium constant, has the dimension 1/concentration, but that cannot be true since the standard Gibbs free energy change, is proportional to the logarithm of K.
This apparent paradox is resolved when the dimension of is defined to be the reciprocal of the dimension of the quotient of concentrations. The implication is that is regarded as having a constant value under all relevant experimental conditions. Nevertheless it is common practice to attach a dimension, such as millimole per litre or micromole per litre, to a value of K that has been determined experimentally.
A Large value indicates that host and guest molecules interact strongly to form the host–guest complex.
Determination of binding constant values and kinetic constant edit
Simple host–guest complexation edit
When the host and guest molecules combine to form a single complex, the equilibrium is represented as
and the equilibrium constant, K, is defined as
where [X] denotes the concentration of a chemical species X (all activity coefficients are assumed to have a numerical values of 1). The mass-balance equations, at any data point,
where and represent the total concentrations, of host and guest, can be reduced to a single quadratic equation in, say, [G] and so can be solved analytically for any given value of K. The concentrations [H] and [HG] can then derived.
The next step in the calculation is to calculate the value, , of a quantity corresponding to the quantity observed . Then, a sum of squares, U, over all data points, np, can be defined as
and this can be minimized with respect to the stability constant value, K, and a parameter such the chemical shift of the species HG (nmr data) or its molar absorbency (uv/vis data). The minimization can be performed in a spreadsheet application such as EXCEL by using the in-built SOLVER utility.
This procedure is applicable to 1:1 adducts.
Nuclear magnetic resonance (NMR) data edit
With nuclear magnetic resonance (NMR) spectra the observed chemical shift value, δ, arising from a given atom contained in a reagent molecule and one or more complexes of that reagent, will be the concentration-weighted average of all shifts of those chemical species. Chemical exchange is assumed to be rapid on the NMR time-scale. terms of mole fractions,
is the chemical shift of the ith chemical species which contains the nucleus and is the concentration /mole fraction ( c is a concentration / mol dm−3) of that species. This expression has the same mathematical form as Beer's law. Chemical shift values may be obtained for more than one nucleus in an analogous way that absorbance may be measured at more than one wavelength. Typical isotopes that may be used in this context are 1H,13C and 31P. It is usual to use a deuterated solvent when measuring 1H chemical shift values.
Absorbance data edit
It is assumed that the absorbance of each species is proportional to the concentration of that species, according to the Beer–Lambert law.
where λ is a wavelength, is the optical path length of the cuvette which contains the solution of the N compounds (chromophores), is the molar absorbance (also known as the extinction coefficient) of the ith chemical species at the wavelength λ, ci is its concentration. When the concentrations have been calculated as above and absorbance has been measured for samples with various concentrations of host and guest, the Beer–Lambert law provides a set of equations, at a given wavelength, that which can be solved by a linear least-squares process for the unknown extinction coefficient values at that wavelength.
Fluorescence data edit
The treatment of this type of data is similar to the treatment of absorbance data. In fact the equation defining the relation between fluorescent intensity and species' concentrations is very similar.
where is the fluorescent intensity of the ith species at unit concentration.
Calorimetry edit
The heat evolved when an aliquot of host solution is added to a solution containing the guest is the sum of contributions from each reaction
where is a measured heat change value (corrected for all extraneous heat contributions) at data point j, is the amount of heat absorbed or emitted when 1 mole of the ith reaction product is formed and is the actual change in the number of moles of that product at that data point. is calculated by solving the equations of mass-balance with given values of the equilibrium constants. If the equilibrium constant values are known, the standard enthalpy change may be calculated by a linear least-squares process, otherwise a non-linear method of data-fitting must be used.
Isothermal titration calorimetry is commonly used to determine the values of both an equilibrium constant and the corresponding standard reaction enthalpy. The manufactures of ITC instruments supply some software with which these quantities may be obtained from experimental data values.
General complexation reaction edit
For each equilibrium involving a host, H, and a guest G
the equilibrium constant, , is defined as
The values of the free concentrations, and are obtained by solving the equations of mass balance with known or estimated values for the stability constants.
Then, the concentrations of each complex species may also be calculated as . The relationship between a species' concentration and the measured quantity is specific for the measurement technique, as indicated in each section above. Using this relationship, the set of parameters, the stability constant values and values of properties such as molar absorptivity or specified chemical shifts, may be refined by a non-linear least-squares refinement process. For a more detailed exposition of the theory see Determination of equilibrium constants. Some dedicated computer programs are listed at Implementations.
Kinetic parameters edit
The binding process is reversible, indicating that the associate constant (ka) is not far larger than disassociate constant (kd). Combing the rate of the reaction, ka, kd, concentration, and time, the relation of the free guest molecule and time can be calculated.[14] By calculating the integration of UV spectrum or NMR,[15][14] the concentration as a function of time curve can be obtained.
Cooperativity edit
In cooperativity, the initial ligand binding affects the host's affinity for subsequent ligands. In positive cooperativity, the first binding event enhances the affinity of the host for another ligand. Examples of positive and negative cooperativity are hemoglobin and aspartate receptor, respectively.[16]
The thermodynamic properties of cooperativity have been studied in order to define mathematical parameters that distinguish positive or negative cooperativity. The traditional Gibbs free energy equation states: . However, to quantify cooperativity in a host–guest system, the binding energy needs to be considered. The schematic on the right shows the binding of A, binding of B, positive cooperative binding of A–B, and lastly, negative cooperative binding of A–B. Therefore, an alternate form of the Gibbs free energy equation would be
where:
- = free energy of binding A
- = free energy of binding B
- = free energy of binding for A and B tethered
- = sum of the free energies of binding
It is considered that if more than the sum of and , it is positively cooperative. If is less, then it is negatively cooperative.[17] Host–guest chemistry is not limited to receptor-lingand interactions. It is also demonstrated in ion-pairing systems. Such interactions are studied in an aqueous media utilizing synthetic organometallic hosts and organic guest molecules. For example, a poly-cationic receptor containing copper (the host) is coordinated with molecules such as tetracarboxylates, tricarballate, aspartate, and acetate (the guests). This study illustrates that entropy rather than enthalpy determines the binding energy of the system leading to negative cooperativity. The large change in entropy originates from the displacement of solvent molecules surrounding the ligand and the receptor. When multiple acetates bind to the receptor, it releases more water molecules to the environment than a tetracarboxylate. This led to a decrease in free energy implying that the system is cooperating negatively.[18] In a similar study, utilizing guanidinium and Cu(II) and polycarboxylate guests, it is demonstrated that positive cooperatively is largely determined by enthalpy.[19] In addition to thermodynamic studies, host–guest chemistry also has biological applications.
Applications edit
Self-healing edit
Because of the non-covalent host-guest interaction, the polymer backbone can have enough flexibility to diffuse. If a crack exists in the materials, after compressing the two materials around the crack, because of the fast exchange of the host-guest molecular structure, the crack will rejoin again revealing good self-healing properties. Harada et al reported a self-healing hydrogel constructed by vinyl-group-modified cyclodextrin and adamantane.[20][22] Another strategy is to use the interaction between the polymer backbone and host molecule (host molecule threading onto the polymer). If the threading process is fast enough, self-healing can also be achieved.[21]
Room-Temperature Phosphorescence edit
Generally, it is not easy to achieve pure organic phosphorescence, partly because of the instability of the triplet state (easily be quenched by moisture, oxygen, etc). Host-guest structures can provide a rigid matrix, which protects the triplet state from being quenched. In this circumstance, α-CD and CB could be used,[23][24] in which the phosphor is served as a guest to interact with the host. For example, 4-phenylpyridium derivatives interacted with CB, and copolymerize with acrylamide. The resulting polymer yielded ~2 s of phosphorescence lifetime. Additionally, Zhu et al used crown ether and potassium ion to modify the polymer, and enhance the emission of phosphorescence.[25]
Stimuli-responsive materials edit
Some guest molecules are charged compounds, which might be oxidized or reduced by certain chemicals. This type of guest molecule can present redox responsiveness. Some host molecules (i.e., α-CD) or guest molecules (i.e., tetra ammonium ion) are pH-sensitive, different pH can result in different species, which significantly influences the binding behavior, giving the material pH responsive properties. Some guest molecules may change their configurations under different lights, which makes the material photo-responsive.[26] Cai et al employed a halogen bond to prepare a host-guest system, and the materials are heat- and mechano-responsive with long persistent emission.[27]
Encryption edit
An encryption system constructed by pillar[5]arene, spiropyran and pentanenitrile (free state and grafted to polymer) was constructed by Wang et al. After UV irradiation, spiropyran would transform into merocyanine. When the visible light was shined on the material, the merocyanine close to the pillar[5]arene-free pentanenitrile complex had faster transformation to spiropyran; on the contrary, the one close to pillar[5]arene-grafted pentanenitrile complex has much slower transformation rate. This spiropyran-merocyanine transformation can be used for message encryption.[28] Another strategy is based on the metallacages and polycyclic aromatic hydrocarbons.[29] Because of the fluorescnece emission differences between the complex and the cages, the information could be encrypted.
Mechanical property edit
Although some host-guest interactions are not strong, increasing the amount of the host-guest interaction can improve the mechanical properties of the materials. As an example, threading the host molecules onto the polymer is one of the commonly used strategies for increasing the mechanical properties of the polymer. It takes time for the host molecules to de-thread from the polymer, which can be a way of energy dissipation.[22][30][31] Another method is to use the slow exchange host-guest interaction. Though the slow exchange improves the mechanical properties, simultaneously, self-healing properties will be sacrificed.[32]
Sensing edit
Traditionally, chemical sensing has been approached with a system that contains a covalently bound indicator to a receptor though a linker. Once the analyte binds, the indicator changes color or fluoresces. This technique is called the indicator-spacer-receptor approach (ISR).[33] In contrast to ISR, indicator-displacement assay (IDA) utilizes a non-covalent interaction between a receptor (the host), indicator, and an analyte (the guest). Similar to ISR, IDA also utilizes colorimetric (C-IDA) and fluorescence (F-IDA) indicators. In an IDA assay, a receptor is incubated with the indicator. When the analyte is added to the mixture, the indicator is released to the environment. Once the indicator is released it either changes color (C-IDA) or fluoresces (F-IDA).[34]
IDA offers several advantages versus the traditional ISR chemical sensing approach. First, it does not require the indicator to be covalently bound to the receptor. Secondly, since there is no covalent bond, various indicators can be used with the same receptor. Lastly, the media in which the assay may be used is diverse.[35]
Chemical sensing techniques such as C-IDA have biological implications. For example, protamine is a coagulant that is routinely administered after cardiopulmonary surgery that counter acts the anti-coagulant activity of herapin. In order to quantify the protamine in plasma samples, a colorimetric displacement assay is used. Azure A dye is blue when it is unbound, but when it is bound to herapin, it shows a purple color. The binding between Azure A and heparin is weak and reversible. This allows protamine to displace Azure A. Once the dye is liberated it displays a purple color. The degree to which the dye is displaced is proportional to the amount of protamine in the plasma.[36]
F-IDA has been used by Kwalczykowski and co-workers to monitor the activities of helicase in E.coli. In this study they used thiazole orange as the indicator. The helicase unwinds the dsDNA to make ssDNA. The fluorescence intensity of thiazole orange has a greater affinity for dsDNA than ssDNA and its fluorescence intensity increases when it is bound to dsDNA than when it is unbound.[37][38]
Conformational switching edit
A crystalline solid has been traditionally viewed as a static entity where the movements of its atomic components are limited to its vibrational equilibrium. As seen by the transformation of graphite to diamond, solid to solid transformation can occur under physical or chemical pressure. It has been proposed that the transformation from one crystal arrangement to another occurs in a cooperative manner.[39][40] Most of these studies have been focused in studying an organic or metal-organic framework.[41][42] In addition to studies of macromolecular crystalline transformation, there are also studies of single-crystal molecules that can change their conformation in the presence of organic solvents. An organometallic complex has been shown to morph into various orientations depending on whether it is exposed to solvent vapors or not.[43]
Environmental applications edit
Host guest systems have been utilized to remove hazardous materials from the environment. They can be made in different sizes and different shapes to trap a variety of chemical guests. One application is the ability of p-tert-butycalix[4]arene to trap a cesium ion. Cesium-137 is radioactive and there is a need to remove it from nuclear waste in an efficient manner. Host–guest chemistry has also been used to remove carcinogenic aromatic amines, and their N-nitroso derivatives from water. These waste materials are used in many industrial processes and found in a variety of products such as: pesticides, drugs, and cosmetics.[44][45]
References edit
- ^ Steed, Jonathan W.; Atwood, Jerry L. (2009). Supramolecular Chemistry (2nd. ed.). Wiley. p. 1002. ISBN 978-0-470-51234-0.
- ^ Lodish, H.; Berk, A.; Kaiser, C. (2008). Molecular Cell Biology. Macmillan. ISBN 978-0-7167-7601-7.
- ^ Freeman, Wade A. (1984). "Structures of the p-xylylenediammonium chloride and calcium hydrogensulfate adducts of the cavitand 'cucurbituril', C36H36N24O12". Acta Crystallographica B. 40 (4): 382–387. doi:10.1107/S0108768184002354.
- ^ Valdés, Carlos; Toledo, Leticia M.; Spitz, Urs; Rebek, Julius (1996). "Structure and Selectivity of a Small Dimeric Encapsulating Assembly". Chem. Eur. J. 2 (8): 989–991. doi:10.1002/chem.19960020814.
- ^ "Supramolecular chemistry", Wikipedia, 2023-01-25, retrieved 2023-02-15
- ^ "The Nobel Prize in Chemistry 1987". NobelPrize.org. Retrieved 2023-02-15.
- ^ "The Nobel Prize in Chemistry 2016". NobelPrize.org. Retrieved 2023-02-15.
- ^ a b c d e f g h i Comprehensive supramolecular chemistry II. J. L. Atwood, George W. Gokel, Leonard J. Barbour. Amsterdam, Netherlands. 2017. ISBN 978-0-12-803199-5. OCLC 992802408.
{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link) - ^ Stoddart, J. F. (1988). "Chapter 12. Host–guest chemistry". Annu. Rep. Prog. Chem., Sect. B: Org. Chem. 85: 353–386. doi:10.1039/OC9888500353. ISSN 0069-3030.
- ^ Harada, Akira (2013), "Supramolecular Polymers (Host-Guest Interactions)", in Kobayashi, Shiro; Müllen, Klaus (eds.), Encyclopedia of Polymeric Nanomaterials, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 1–5, doi:10.1007/978-3-642-36199-9_54-1, ISBN 978-3-642-36199-9, retrieved 2023-02-15
- ^ a b Seale, James S. W.; Feng, Yuanning; Feng, Liang; Astumian, R. Dean; Stoddart, J. Fraser (2022). "Polyrotaxanes and the pump paradigm". Chemical Society Reviews. 51 (20): 8450–8475. doi:10.1039/D2CS00194B. ISSN 0306-0012. PMID 36189715. S2CID 252682455.
- ^ a b Anslyn, Eric V.; Dougherty, Dennis A. (2005). Modern Physical Organic Chemistry. MacMillan. ISBN 978-1-891389-31-3.
- ^ Piñeiro, Á.; Banquy, X.; Pérez-Casas, S.; Tovar, É.; García, A.; Villa, A.; Amigo, A.; Mark, A. E.; Costas, M. (2007). "On the Characterization of Host–Guest Complexes: Surface Tension, Calorimetry, and Molecular Dynamics of Cyclodextrins with a Non-ionic Surfactant". Journal of Physical Chemistry B. 111 (17): 4383–92. doi:10.1021/jp0688815. PMID 17428087.
- ^ a b Herrmann, W.; Keller, B.; Wenz, G. (1997-08-01). "Kinetics and Thermodynamics of the Inclusion of Ionene-6,10 in α-Cyclodextrin in an Aqueous Solution". Macromolecules. 30 (17): 4966–4972. Bibcode:1997MaMol..30.4966H. doi:10.1021/ma961373g. ISSN 0024-9297.
- ^ Puig-Rigall, Joan; Serra-Gómez, Rafael; Stead, Ian; Grillo, Isabelle; Dreiss, Cécile A.; González-Gaitano, Gustavo (2019-02-26). "Pseudo-Polyrotaxanes of Cyclodextrins with Direct and Reverse X-Shaped Block Copolymers: A Kinetic and Structural Study". Macromolecules. 52 (4): 1458–1468. Bibcode:2019MaMol..52.1458P. doi:10.1021/acs.macromol.8b02509. ISSN 0024-9297. S2CID 104324504.
- ^ Koshland, D (1996). "The structural basis of negative cooperativity: receptors and enzymes". Current Opinion in Structural Biology. 6 (6): 757–761. doi:10.1016/S0959-440X(96)80004-2. PMID 8994875.
- ^ Jencks, W. P. (1981). "On the attribution and additivity of binding energies". Proceedings of the National Academy of Sciences, USA. 78 (7): 4046–4050. Bibcode:1981PNAS...78.4046J. doi:10.1073/pnas.78.7.4046. PMC 319722. PMID 16593049.
- ^ Dobrzanska, L; Lloyd, G; Esterhuysen, C; Barbour, L (2003). "Studies into the Thermodynamic Origin of Negative Cooperativity in Ion-Pairing Molecular Recognition". Journal of the American Chemical Society. 125 (36): 10963–10970. doi:10.1021/ja030265o. PMID 12952478.
- ^ Hughes, A.; Anslyn, E (2007). "A cationic host displaying positive cooperativity in water". Proceedings of the National Academy of Sciences, USA. 104 (16): 6538–6543. Bibcode:2007PNAS..104.6538H. doi:10.1073/pnas.0609144104. PMC 1871821. PMID 17420472.
- ^ a b Ikura, Ryohei; Park, Junsu; Osaki, Motofumi; Yamaguchi, Hiroyasu; Harada, Akira; Takashima, Yoshinori (December 2022). "Design of self-healing and self-restoring materials utilizing reversible and movable crosslinks". NPG Asia Materials. 14 (1): 10. Bibcode:2022npjAM..14...10I. doi:10.1038/s41427-021-00349-1. ISSN 1884-4049.
- ^ a b Xie, Jing; Yu, Peng; Wang, Zhanhua; Li, Jianshu (2022-03-14). "Recent Advances of Self-Healing Polymer Materials via Supramolecular Forces for Biomedical Applications". Biomacromolecules. 23 (3): 641–660. doi:10.1021/acs.biomac.1c01647. ISSN 1525-7797. PMID 35199999. S2CID 247082155.
- ^ a b Park, Junsu; Murayama, Shunsuke; Osaki, Motofumi; Yamaguchi, Hiroyasu; Harada, Akira; Matsuba, Go; Takashima, Yoshinori (October 2020). "Extremely Rapid Self‐Healable and Recyclable Supramolecular Materials through Planetary Ball Milling and Host–Guest Interactions". Advanced Materials. 32 (39): 2002008. doi:10.1002/adma.202002008. ISSN 0935-9648. PMID 32844527. S2CID 221326154.
- ^ Yan, Xi; Peng, Hao; Xiang, Yuan; Wang, Juan; Yu, Lan; Tao, Ye; Li, Huanhuan; Huang, Wei; Chen, Runfeng (January 2022). "Recent Advances on Host–Guest Material Systems toward Organic Room Temperature Phosphorescence". Small. 18 (1): 2104073. doi:10.1002/smll.202104073. ISSN 1613-6810. PMID 34725921. S2CID 240421091.
- ^ Xu, Wen‐Wen; Chen, Yong; Lu, Yi‐Lin; Qin, Yue‐Xiu; Zhang, Hui; Xu, Xiufang; Liu, Yu (February 2022). "Tunable Second‐Level Room‐Temperature Phosphorescence of Solid Supramolecules between Acrylamide–Phenylpyridium Copolymers and Cucurbit[7]uril". Angewandte Chemie International Edition. 61 (6): e202115265. doi:10.1002/anie.202115265. ISSN 1433-7851. PMID 34874598. S2CID 244922727.
- ^ Zhu, Weijie; Xing, Hao; Li, Errui; Zhu, Huangtianzhi; Huang, Feihe (2022-11-08). "Room-Temperature Phosphorescence in the Amorphous State Enhanced by Copolymerization and Host–Guest Complexation". Macromolecules. 55 (21): 9802–9809. Bibcode:2022MaMol..55.9802Z. doi:10.1021/acs.macromol.2c00680. ISSN 0024-9297. S2CID 253051272.
- ^ Blanco-Gómez, Arturo; Cortón, Pablo; Barravecchia, Liliana; Neira, Iago; Pazos, Elena; Peinador, Carlos; García, Marcos D. (2020). "Controlled binding of organic guests by stimuli-responsive macrocycles". Chemical Society Reviews. 49 (12): 3834–3862. doi:10.1039/D0CS00109K. hdl:2183/31671. ISSN 0306-0012. PMID 32395726. S2CID 218599759.
- ^ Dai, Wenbo; Niu, Xiaowei; Wu, Xinghui; Ren, Yue; Zhang, Yongfeng; Li, Gengchen; Su, Han; Lei, Yunxiang; Xiao, Jiawen; Shi, Jianbing; Tong, Bin; Cai, Zhengxu; Dong, Yuping (2022-03-21). "Halogen Bonding: A New Platform for Achieving Multi‐Stimuli‐Responsive Persistent Phosphorescence". Angewandte Chemie International Edition. 61 (13): e202200236. doi:10.1002/anie.202200236. ISSN 1433-7851. PMID 35102661. S2CID 246443916.
- ^ Ju, Huaqiang; Zhu, Chao Nan; Wang, Hu; Page, Zachariah A.; Wu, Zi Liang; Sessler, Jonathan L.; Huang, Feihe (February 2022). "Paper without a Trail: Time‐Dependent Encryption using Pillar[5]arene‐Based Host–Guest Invisible Ink". Advanced Materials. 34 (6): 2108163. Bibcode:2022AdM....3408163J. doi:10.1002/adma.202108163. ISSN 0935-9648. PMID 34802162. S2CID 244482426.
- ^ Hou, Yali; Zhang, Zeyuan; Lu, Shuai; Yuan, Jun; Zhu, Qiangyu; Chen, Wei-Peng; Ling, Sanliang; Li, Xiaopeng; Zheng, Yan-Zhen; Zhu, Kelong; Zhang, Mingming (2020-11-04). "Highly Emissive Perylene Diimide-Based Metallacages and Their Host–Guest Chemistry for Information Encryption". Journal of the American Chemical Society. 142 (44): 18763–18768. doi:10.1021/jacs.0c09904. ISSN 0002-7863. PMID 33085462. S2CID 224824066.
- ^ Jin, Jia‐Ni; Yang, Xi‐Ran; Wang, Yan‐Fang; Zhao, Lei‐Min; Yang, Liu‐Pan; Huang, Liping; Jiang, Wei (2023-01-18). "Mechanical Training Enabled Reinforcement of Polyrotaxane‐Containing Hydrogel". Angewandte Chemie. 135 (8). doi:10.1002/ange.202218313. ISSN 0044-8249.
- ^ Wang, Shuaipeng; Chen, Yong; Sun, Yonghui; Qin, Yuexiu; Zhang, Hui; Yu, Xiaoyong; Liu, Yu (2022-01-20). "Stretchable slide-ring supramolecular hydrogel for flexible electronic devices". Communications Materials. 3 (1): 2. Bibcode:2022CoMat...3....2W. doi:10.1038/s43246-022-00225-7. ISSN 2662-4443.
- ^ Huang, Zehuan; Chen, Xiaoyi; O’Neill, Stephen J. K.; Wu, Guanglu; Whitaker, Daniel J.; Li, Jiaxuan; McCune, Jade A.; Scherman, Oren A. (January 2022). "Highly compressible glass-like supramolecular polymer networks". Nature Materials. 21 (1): 103–109. Bibcode:2022NatMa..21..103H. doi:10.1038/s41563-021-01124-x. ISSN 1476-1122. PMID 34819661. S2CID 244532641.
- ^ de Silva, A.P.; McCaughan, B; McKinney, B.O. F.; Querol, M. (2003). "Newer optical-based molecular devices from older coordination chemistry". Dalton Transactions. 10 (10): 1902–1913. doi:10.1039/b212447p.
- ^ Anslyn, E. (2007). "Supramolecular Analytical Chemistry". Journal of Organic Chemistry. 72 (3): 687–699. doi:10.1021/jo0617971. PMID 17253783.
- ^ Nguyen, B.; Anslyn, E. (2006). "Indicator-displacement assays". Coord. Chem. Rev. 250 (23–24): 3118–3127. doi:10.1016/j.ccr.2006.04.009.
- ^ Yang, V.; Fu, Y.; Teng, C.; Ma, S.; Shanberge, J. (1994). "A method for the quantitation of protamine in plasma" (PDF). Thrombosis Research. 74 (4): 427–434. doi:10.1016/0049-3848(94)90158-9. hdl:2027.42/31577. PMID 7521974.
- ^ Eggleston, A.; Rahim, N.; Kowalczykowski, S; Ma, S.; Shanberge, J. (1996). "A method for the quantitation of protamine in plasma". Nucleic Acids Research. 24 (7): 1179–1186. doi:10.1093/nar/24.7.1179. PMC 145774. PMID 8614617.
- ^ Biancardi, Alessandro; Tarita, Biver; Alberto, Marini; Benedetta, Mennucci; Fernando, Secco (2011). "Thiazole orange (TO) as a light-switch probe: a combined quantum-mechanical and spectroscopic study". Physical Chemistry Chemical Physics. 13 (27): 12595–12602. Bibcode:2011PCCP...1312595B. doi:10.1039/C1CP20812H. PMID 21660321.
- ^ Atwood, J; Barbour, L; Jerga, A; Schottel, L (2002). "Guest Transport in a nonporous Organic Solid via Dynamic van der Waals Cooperativity". Science. 298 (5595): 1000–1002. Bibcode:2002Sci...298.1000A. doi:10.1126/science.1077591. PMID 12411698. S2CID 17584598.
- ^ Kitagawa, S; Uemura, K (2005). "Dynamic porous properties of coordination polymers inspired by hydrogen bonds". Chemical Society Reviews. 34 (2): 109–119. doi:10.1039/b313997m. PMID 15672175.
- ^ Sozzani, P; Bracco, S; Commoti, A; Ferretti, R; Simonutti, R (2005). "Methane and Carbon Dioxide Storage in a Porous van der Waals Crystal". Angewandte Chemie. 44 (12): 1816–1820. doi:10.1002/anie.200461704. PMID 15662674.
- ^ Uemura, K; Kitagawa, S; Fukui, K; Saito, K (2004). "A Contrivance for a Dynamic Porous Framework: Cooperative Guest Adsorption Based on Square Grids Connected by Amide−Amide Hydrogen Bonds". J. Am. Chem. Soc. 126 (12): 3817–3828. doi:10.1021/ja039914m. PMID 15038736.
- ^ Dobrzanska, L; Lloyd, G; Esterhuysen, C; Barbour, L (2006). "Guest-Induced Conformational Switching in a Single Crystal". Angewandte Chemie. 45 (35): 5856–5859. doi:10.1002/anie.200602057. PMID 16871642.
- ^ Eric Hughes; Jason Jordan; Terry Gullion (2001). "Structural Characterization of the [Cs(p-tert-butylcalix[4]arene -H) (MeCN)] Guest–Host System by 13C-133Cs REDOR NMR". Journal of Physical Chemistry B. 105 (25): 5887–5891. doi:10.1021/jp004559x.
- ^ Serkan Erdemir; Mufit Bahadir; Mustafa Yilmaz (2009). "Extraction of Carcinogenic Aromatic Amines from Aqueous Solution Using Calix[n]arene Derivatives as Carriers". Journal of Hazardous Materials. 168 (2–3): 1170–1176. doi:10.1016/j.jhazmat.2009.02.150. PMID 19345489.