| Great dodecahemidodecahedron | |
|---|---|
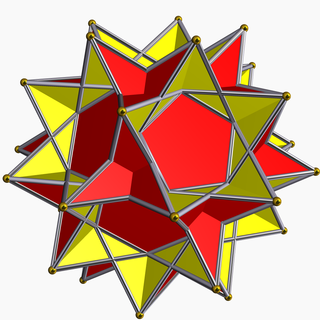
| |
| Type | Uniform star polyhedron |
| Elements | F = 18, E = 60 V = 30 (χ = −12) |
| Faces by sides | 12{5/2}+6{10/3} |
| Coxeter diagram | |
| Wythoff symbol | 5/3 5/2 | 5/3 (double covering) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U70, C86, W107 |
| Dual polyhedron | Great dodecahemidodecacron |
| Vertex figure |  5/2.10/3.5/3.10/3 |
| Bowers acronym | Gidhid |
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices.[1] Its vertex figure is a crossed quadrilateral.

Aside from the regular small stellated dodecahedron {5/2,5} and great stellated dodecahedron {5/2,3}, it is the only nonconvex uniform polyhedron whose faces are all non-convex regular polygons (star polygons), namely the star polygons {5/2} and {10/3}.
It is a hemipolyhedron with 6 decagrammic faces passing through the model center.
Related polyhedra edit
Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the great icosidodecahedron (having the pentagrammic faces in common) and the great icosihemidodecahedron (having the decagrammic faces in common).
| Great icosidodecahedron |
Great dodecahemidodecahedron |
Great icosihemidodecahedron |
| Icosidodecahedron (convex hull) |
Gallery edit
| Traditional filling |
Modulo-2 filling |
See also edit
References edit
- ^ Maeder, Roman. "70: great dodecahemidodecahedron". MathConsult.