The term Great Year has more than one major meaning. It is defined by scientific astronomy as "The period of one complete cycle of the equinoxes around the ecliptic, or about 25,800 years". Ptolemy reported that his teacher Hipparchus, by comparing the position of the vernal equinox against the fixed stars in his time and in earlier observations, discovered that it shifts westward approximately one degree every 72 years. Thus the time it would take the equinox to make a complete revolution through all the zodiac constellations and return to its original position would be approximately 25,920 years. In the heliocentric model, the precession can be pictured as the axis of the Earth's rotation making a slow revolution around the normal to the plane of the ecliptic. The position of the Earth's axis in the northern night sky currently almost aligns with the star Polaris, the North Star. But as the direction of the axis is changing, this is a passing coincidence which was not always so and will not be so again until a Great Year has passed.
The Platonic Year,[1] which is also called the Great Year, has a different more ancient and mystical meaning. Plato hypothesized that winding the orbital motions of the Sun, Moon and naked eye planets forward or back in time would arrive at a point where they are in the same positions as they are today. He called this time period the Great Year and suggested that such a unified return would take place about every 36,000 years.
By extension, the term "Great Year" can be used for any concept of eternal return in the world's mythologies or philosophies. Historian Otto Neugebauer writes:
The difficulty with the term "great year" lies in its ambiguity. Almost any period can be found sometime or somewhere honored with this name.[2]
Description of the science edit
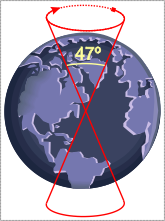
The plane of the ecliptic is the plane described by the apparent motion of the Sun against the starry background. It is the Earth's orbital motion about the Sun which causes this apparent motion to occur. The Earth's axis of rotation is not set perpendicular to this plane but at a present angle of 23.5 degrees to the perpendicular. The alignment of the axis is maintained throughout the year so that the point of sky above the north or south poles remains unchanged throughout the Earth's annual rotation around the Sun.[3]
A slow conical motion of the Earth's polar axis about its normal to the plane of the ecliptic is caused by the attractive force of the other heavenly bodies on the equatorial protuberance of the Earth. A similar conical motion can also be observed in a gyroscope that is subjected to lateral forces.
The resultant motion of the Earth's axis is called general precession and the equinox points in the ecliptic move westward along the ecliptic at the rate of about 50.3 seconds of arc per year as a result. In 25,772 years, the points are once again at the same point in the sky where observations began.[1]
In addition the tilt, or obliquity, of the Earth's axis is not constant but changes in a cycle of its own. During a cycle that averages about 40,000 years, the tilt of the axis varies between 22.1 and 24.5 degrees.[4]
History of both definitions edit
Plato (c. 360 BC) used the term "perfect year" to describe the return of the celestial bodies (planets) and the diurnal rotation of the fixed stars (circle of the Same) to their original positions; there is no evidence he had any knowledge of axial precession.[5] The cycle which Plato describes is one of planetary and astral conjunction, which can be postulated without any awareness of axial precession.
Hipparchus (c. 120 BC) is the first Greek credited with discovering axial precession roughly two hundred years after Plato's death (see below).
Cicero (1st century BC) followed Plato in defining the Great Year as a combination of solar, lunar and planetary cycles.[6][7]
Plato's description of the perfect year is found in his dialogue Timaeus:
And so people are all but ignorant of the fact that time really is the wanderings of these bodies, bewilderingly numerous as they are and astonishingly variegated. It is none the less possible, however, to discern that the perfect number of time brings to completion the perfect year at that moment when the relative speeds of all eight periods have been completed together and, measured by the circle of the Same that moves uniformly, have achieved their consummation."[8]
In De Natura Deorum, Cicero wrote
On the diverse motions of the planets the mathematicians have based what they call the Great Year, "which is completed when the sun, moon and five planets having all finished their courses have returned to the same positions relative to one another. The length of this period is hotly debated, but it must necessarily be a fixed and definite time."[6]
Macrobius (early fifth century AD) in his commentary on Cicero's Somnium Scipionis states that 'the philosophers' reckon the Great Year as 15,000 years.[9]
Censorinus (3rd century AD) wrote that Aristarchus of Samos reckoned a Great Year as 2484 years: but it has been argued that this is a miscopying of 2434, which represents 45 Exeligmos cycles.[9][10]
The origin of the Platonic Year would seem to have no connection with the precession of the equinoxes as this was unknown in Plato's time.[11] Two centuries after Plato, Hipparchus is credited with discovering the period of equinox precession,[12] and the term "Great Year" eventually came to be applied to the period of that precession caused by the slow gyration of the Earth's axis.
Some time around the middle of the second century BC, the astronomer Hipparchus discovered that the fixed stars as a whole gradually shifted their position in relation to the annually determined locations of the Sun at the equinoxes and solstices... Otto Neugebauer argued that Hipparchus in fact believed that this [36,000 years] was the maximum figure and that he also computed the true rate of one complete precession cycle at just under 26,000 years...[13]
It is argued that a confusion between the two originated with the astronomer Ptolemy (c. 170 AD), who "adopted the larger, erroneous, figure, with the result that henceforth the two versions of the Great Year — the Platonic Great Year, defined by the planets, and the precessional, defined by the stars — were to be increasingly confused."[14]
Ptolemy has even been accused of committing scientific fraud by making up observations that would give the figure of 36,000 years even though the data available to him were good enough to get very near the true figure of 26,000.[15]
Josephus (first century AD) refers to a 'Great Year' (Ancient Greek: μέγας ἐνιαυτός) of 600 years.[16]
God afforded them a longer time of life on account of their virtue, and the good use they made of it in astronomical and geometrical discoveries, which would not have afforded the time of foretelling [the periods of the stars] unless they had lived six hundred years; for the great year is completed in that interval.[16]
It has been suggested that he obtained this value from Berossos (c. 3rd century BC) who reckoned time in intervals of 60, 600 and 3600 years.[17]
Isaac Newton (1642 – 1726/27) determined the cause of precession and established the rate of precession at 1 degree per 72 years, very close to the best value measured today, thus demonstrating the magnitude of the error in the earlier value of 1 degree per century.[18]
See also edit
- Astrological age – Time period in ancient historical and astrological theories of time
- Axial precession – Change of rotational axis in an astronomical body (Precession § Astronomy)
- Yuga – Age or era in Hinduism
References edit
- ^ a b "Aerospace Science and Technology Dictionary G Section". Hq.nasa.gov. 1989-10-18. Archived from the original on 2005-04-21. Retrieved 2014-03-02.
- ^ Neugebauer O., (1975) A History of Ancient mathematical astronomy, Birkhäuser, p.618
- ^ "Aerospace Science and Technonlogy Dictionary P Section". www.hq.nasa.gov. Archived from the original on 2005-04-21. Retrieved 2019-02-09.
- ^ "Milutin Milankovitch". earthobservatory.nasa.gov. 2000-03-24. Retrieved 2019-02-15.
- ^ Wood, Michael (2010-06-24). The Platonic Year. Oxford University Press. doi:10.1093/acprof:oso/9780199557660.001.0001. ISBN 9780191701726.
- ^ a b Cicero, De Natura Deorum II.51. "Full text with an English translation by H. Rackham". 1933. Retrieved 2019-11-13.
- ^ Nicholas Campion, "The Great Year: Astrology, Millenarianism and History in the Western Tradition" (Arkana/Penguin Books, 1994), p. 6.
- ^ Plato, Timaeus 39d, in John M. Cooper (ed.), "Plato: Complete Works" (Hackett Publishing Company, 1997), p. 1243
- ^ a b J. D. North (1989). Stars, Mind & Fate: Essays in Ancient and Mediaeval Cosmology. Bloomsbury Academic. p. 96. ISBN 978-0-907628-94-1.
- ^ Aristarchos & System B 2002, DIO 11.1 May 31 (p. 6) Comments on the Aristarchan Evidence
- ^ William Harris Stahl, "Macrobius: Commentary on the Dream of Scipio" (Columbia University Press, 1952), p. 21
- ^ "Aerospace Science and Technology Dictionary G Section". Hq.nasa.gov. 1989-10-18. Archived from the original on 2005-04-21. Retrieved 2015-08-23.
- ^ Nicholas Campion, "The Great Year: Astrology, Millenarianism and History in the Western Tradition" (Arkana/Penguin Books, 1994), p.246.
- ^ Nicholas Campion, "The Great Year: Astrology, Millenarianism and History in the Western Tradition" (Arkana/Penguin Books, 1994), p. 246–247.
- ^ R.R.Newton, "The Authenticity of Ptolemy's star data"
- ^ a b Josephus – Antiquities of the Jews – Book I, Chapter 3, Paragraph 9
- ^ Josephus, Jewish Antiquities, Loeb, p.1, note a
- ^ "Internet History Sourcebooks". Fordham.edu. p. letter 17. Retrieved 2014-03-02.
Further reading edit
- Callatay, G. de (1996). Annus Platonicus, A Study of World Cycles in Greek Latin and Arabian Sources. Louvain: l'Institut Orientaliste de Louvain.
- Campion, Nicholas (1994). The Great Year. Penguin. ISBN 0140192964.
- Cristoff, Boris (1981). Roca, Martínez (ed.). El destino de la humanidad. Barcelona: colección Fontana.
- Mcevilley, Thomas C. (2001). "Chapter 3: The Cosmic Cycle". The Shape of Ancient Thought: Comparative Studies in Greek and Indian Philosophy. Allworth. ISBN 1581152035.