This article includes a list of general references, but it lacks sufficient corresponding inline citations. (June 2017) |
In mathematics, a filter or order filter is a special subset of a partially ordered set (poset), describing "large" or "eventual" elements. Filters appear in order and lattice theory, but also topology, whence they originate. The notion dual to a filter is an order ideal.
Special cases of filters include ultrafilters, which are filters that cannot be enlarged, and describe nonconstructive techniques in mathematical logic.
Filters on sets were introduced by Henri Cartan in 1937. Nicolas Bourbaki, in their book Topologie Générale, popularized filters as an alternative to E. H. Moore and Herman L. Smith's 1922 notion of a net; order filters generalize this notion from the specific case of a power set under inclusion to arbitrary partially ordered sets. Nevertheless, the theory of power-set filters retains interest in its own right, in part for substantial applications in topology.
Motivation edit
Fix a partially ordered set (poset) P. Intuitively, a filter F is a subset of P whose members are elements large enough to satisfy some criterion.[1] For instance, if x ∈ P, then the set of elements above x is a filter, called the principal filter at x. (If x and y are incomparable elements of P, then neither the principal filter at x nor y is contained in the other.)
Similarly, a filter on a set S contains those subsets that are sufficiently large to contain some given thing. For example, if S is the real line and x ∈ S, then the family of sets including x in their interior is a filter, called the neighborhood filter at x. The thing in this case is slightly larger than x, but it still does not contain any other specific point of the line.
The above considerations motivate the upward closure requirement in the definition below: "large enough" objects can always be made larger.
To understand the other two conditions, reverse the roles and instead consider F as a "locating scheme" to find x. In this interpretation, one searches in some space X, and expects F to describe those subsets of X that contain the goal. The goal must be located somewhere; thus the empty set ∅ can never be in F. And if two subsets both contain the goal, then should "zoom in" to their common region.
An ultrafilter describes a "perfect locating scheme" where each scheme component gives new information (either "look here" or "look elsewhere"). Compactness is the property that "every search is fruitful," or, to put it another way, "every locating scheme ends in a search result."
A common use for a filter is to define properties that are satisfied by "generic" elements of some topological space.[2] This application generalizes the "locating scheme" to find points that might be hard to write down explicitly.
Definition edit
A subset F of a partially ordered set (P, ≤) is a filter or dual ideal if the following are satisfied:
- Nontriviality
- The set F is non-empty.
- Downward directed
- For every x, y ∈ F, there is some z ∈ F such that z ≤ x and z ≤ y.
- Upward closure
- For every x ∈ F and p ∈ P, the condition x ≤ p implies p ∈ F.
If, additionally, F ≠ P, then F is said to be a proper filter. Authors in set theory and mathematical logic often require all filters to be proper; this article will eschew that convention.[3] An ultrafilter is a filter contained in no other proper filter.
Filter bases edit
A subset S of F is a base or basis for F if the upper set generated by S (i.e., the smallest upwards-closed set containing S) is all of F. Every filter is a base for itself.
Moreover, if B ⊆ P is nonempty and downward directed, then B generates an upper set F that is a filter (for which B is a base). Such sets are called prefilters, as well as the aforementioned filter base/basis, and F is said to be generated or spanned by B. A prefilter is proper if and only if it generates a proper filter.
Given p ∈ P, the set {x : p ≤ x} is the smallest filter containing p, and sometimes written ↑ p. Such a filter is called a principal filter; p is said to be the principal element of F, or generate F.
Refinement edit
Suppose B and C are two prefilters on P, and, for each c ∈ C, there is a b ∈ B, such that b ≤ c. Then we say that B is finer than (or refines) C; likewise, C is coarser than (or coarsens) B. Refinement is a preorder on the set of prefilters. In fact, if C also refines B, then B and C are called equivalent, for they generate the same filter. Thus passage from prefilter to filter is an instance of passing from a preordering to associated partial ordering.
Special cases edit
Historically, filters generalized to order-theoretic lattices before arbitrary partial orders. In the case of lattices, downward direction can be written as closure under finite meets: for all x, y ∈ F, one has x ∧ y ∈ F.[4]
Linear filters edit
A linear (ultra)filter is an (ultra)filter on the lattice of vector subspaces of a given vector space, ordered by inclusion. Explicitly, a linear filter on a vector space X is a family B of vector subspaces of X such that if A, B ∈ B and C is a vector subspace of X that contains A, then A ∩ B ∈ B and C ∈ B.[5]
A linear filter is proper if it does not contain {0}.[5]
Filters on a set; subbases edit
| Families of sets over | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Is necessarily true of or, is closed under: |
Directed by |
F.I.P. | ||||||||
| π-system | ||||||||||
| Semiring | Never | |||||||||
| Semialgebra (Semifield) | Never | |||||||||
| Monotone class | only if | only if | ||||||||
| 𝜆-system (Dynkin System) | only if |
only if or they are disjoint |
Never | |||||||
| Ring (Order theory) | ||||||||||
| Ring (Measure theory) | Never | |||||||||
| δ-Ring | Never | |||||||||
| 𝜎-Ring | Never | |||||||||
| Algebra (Field) | Never | |||||||||
| 𝜎-Algebra (𝜎-Field) | Never | |||||||||
| Dual ideal | ||||||||||
| Filter | Never | Never | ||||||||
| Prefilter (Filter base) | Never | Never | ||||||||
| Filter subbase | Never | Never | ||||||||
| Open Topology | (even arbitrary ) |
Never | ||||||||
| Closed Topology | (even arbitrary ) |
Never | ||||||||
| Is necessarily true of or, is closed under: |
directed downward |
finite intersections |
finite unions |
relative complements |
complements in |
countable intersections |
countable unions |
contains | contains | Finite Intersection Property |
|
Additionally, a semiring is a π-system where every complement is equal to a finite disjoint union of sets in | ||||||||||
Given a set S, the power set P(S) is partially ordered by set inclusion; filters on this poset are often just called "filters on S," in an abuse of terminology. For such posets, downward direction and upward closure reduce to:[3]
- Closure under finite intersections
- If A, B ∈ F, then so too is A ∩ B ∈ F.
- Isotony
- [6] If A ∈ F and A ⊆ B ⊆ S, then B ∈ F.
A proper[7]/non-degenerate[8] filter is one that does not contain ∅, and these three conditions (including non-degeneracy) are Henri Cartan's original definition of a filter.[9][10] It is common — though not universal — to require filters on sets to be proper (whatever one's stance on poset filters); we shall again eschew this convention.
Prefilters on a set are proper if and only if they do not contain ∅ either.
For every subset T of P(S), there is a smallest filter F containing T. As with prefilters, T is said to generate or span F; a base for F is the set U of all finite intersections of T. The set T is said to be a filter subbase when F (and thus U) is proper.
Proper filters on sets have the finite intersection property.
If S = ∅, then S admits only the improper filter {∅}.
Free filters edit
A filter is said to be a free if the intersection of its members is empty. A proper principal filter is not free.
Since the intersection of any finite number of members of a filter is also a member, no proper filter on a finite set is free, and indeed is the principal filter generated by the common intersection of all of its members. But a nonprincipal filter on an infinite set is not necessarily free: a filter is free if and only if it includes the Fréchet filter (see § Examples).
Examples edit
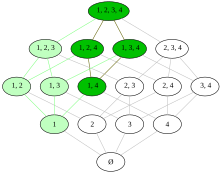
See the image at the top of this article for a simple example of filters on the finite poset P({1, 2, 3, 4}).
Partially order ℝ → ℝ, the space of real-valued functions on ℝ, by pointwise comparison. Then the set of functions "large at infinity,"
The set {{k : k ≥ N} : N ∈ ℕ} is a filter in P(ℕ). More generally, if D is any directed set, then
The Fréchet filter on an infinite set X is
Given an ordinal a, a subset of a is called a club if it is closed in the order topology of a but has net-theoretic limit a. The clubs of a form a filter: the club filter, ♣(a).
The previous construction generalizes as follows: any club C is also a collection of dense subsets (in the ordinal topology) of a, and ♣(a) meets each element of C. Replacing C with an arbitrary collection C̃ of dense sets, there "typically" exists a filter meeting each element of C̃, called a generic filter. For countable C̃, the Rasiowa–Sikorski lemma implies that such a filter must exist; for "small" uncountable C̃, the existence of such a filter can be forced through Martin's axiom.
Let P denote the set of partial orders of limited cardinality, modulo isomorphism. Partially order P by:
- A ≤ B if there exists a strictly increasing f : A → B.
Then the subset of non-atomic partial orders forms a filter. Likewise, if I is the set of injective modules over some given commutative ring, of limited cardinality, modulo isomorphism, then a partial order on I is:
- A ≤ B if there exists an injective linear map f : A → B.[11]
Given any infinite cardinal κ, the modules in I that cannot be generated by fewer than κ elements form a filter.
Every uniform structure on a set X is a filter on X × X.
Relationship to ideals edit
The dual notion to a filter — that is, the concept obtained by reversing all ≤ and exchanging ∧ with ∨ — is an order ideal. Because of this duality, any question of filters can be mechanically translated to a question about ideals and vice-versa; in particular, a prime or maximal filter is a filter whose corresponding ideal is (respectively) prime or maximal.
A filter is an ultrafilter if and only if the corresponding ideal is minimal.
In model theory edit
For every filter F on a set S, the set function defined by
In topology edit
In general topology and analysis, filters are used to define convergence in a manner similar to the role of sequences in a metric space. They unify the concept of a limit across the wide variety of arbitrary topological spaces.
To understand the need for filters, begin with the equivalent concept of a net. A sequence is usually indexed by the natural numbers ℕ, which are a totally ordered set. Nets generalize the notion of a sequence by replacing ℕ with an arbitrary directed set. In certain categories of topological spaces, such as first-countable spaces, sequences characterize most topological properties, but this is not true in general. However, nets — as well as filters — always do characterize those topological properties.
Filters do not involve any set external to the topological space X, whereas sequences and nets rely on other directed sets. For this reason, the collection of all filters on X is always a set, whereas the collection of all X-valued nets is a proper class.
Neighborhood bases edit
Any point x in the topological space X defines a neighborhood filter or system Nx: namely, the family of all sets containing x in their interior. A set N of neighborhoods of x is a neighborhood base at x if N generates Nx. Equivalently, S ⊆ X is a neighborhood of x if and only if there exists N ∈ N such that N ⊆ S.
Convergent filters and cluster points edit
A prefilter B converges to a point x, written B → x, if and only if B generates a filter F that contains the neighborhood filter Nx — explicitly, for every neighborhood U of x, there is some V ∈ B such that V ⊆ U. Less explicitly, B → x if and only if B refines Nx, and any neighborhood base at x can replace Nx in this condition. Clearly, every neighborhood base at x converges to x.
A filter F (which generates itself) converges to x if Nx ⊆ F. The above can also be reversed to characterize the neighborhood filter Nx: Nx is the finest filter coarser than each filter converging to x.
If B → x, then x is called a limit (point) of B. The prefilter B is said to cluster at x (or have x as a cluster point) if and only if each element of B has non-empty intersection with each neighborhood of x. Every limit point is a cluster point but the converse is not true in general. However, every cluster point of an ultrafilter is a limit point.
See also edit
- Filtration (mathematics)
- Filtration (probability theory) – Model of information available at a given point of a random process
- Filtration (abstract algebra)
- Generic filter – in set theory, given a collection of dense open subsets of a poset, a filter that meets all sets in that collection
- Ideal (set theory) – Non-empty family of sets that is closed under finite unions and subsets
Notes edit
- ^ Koutras et al. 2021.
- ^ Igarashi, Ayumi; Zwicker, William S. (16 February 2021). "Fair division of graphs and of tangled cakes". arXiv:2102.08560 [math.CO].
- ^ a b Dugundji 1966, pp. 211–213.
- ^ Davey, B. A.; Priestley, H. A. (1990). Introduction to Lattices and Order. Cambridge Mathematical Textbooks. Cambridge University Press. p. 184.
- ^ a b Bergman & Hrushovski 1998.
- ^ Dolecki & Mynard 2016, pp. 27–29.
- ^ Goldblatt, R. Lectures on the Hyperreals: an Introduction to Nonstandard Analysis. p. 32.
- ^ Narici & Beckenstein 2011, pp. 2–7.
- ^ Cartan 1937a.
- ^ Cartan 1937b.
- ^ Bumby, R. T. (1965-12-01). "Modules which are isomorphic to submodules of each other". Archiv der Mathematik. 16 (1): 184–185. doi:10.1007/BF01220018. ISSN 1420-8938.
References edit
- Nicolas Bourbaki, General Topology (Topologie Générale), ISBN 0-387-19374-X (Ch. 1–4): Provides a good reference for filters in general topology (Chapter I) and for Cauchy filters in uniform spaces (Chapter II)
- Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 3-540-13627-4. OCLC 17499190.
- Burris, Stanley; Sankappanavar, Hanamantagouda P. (2012). A Course in Universal Algebra (PDF). Springer-Verlag. ISBN 978-0-9880552-0-9. Archived from the original on 1 April 2022.
- Cartan, Henri (1937a). "Théorie des filtres". Comptes rendus hebdomadaires des séances de l'Académie des sciences. 205: 595–598.
- Cartan, Henri (1937b). "Filtres et ultrafiltres". Comptes rendus hebdomadaires des séances de l'Académie des sciences. 205: 777–779.
- Dolecki, Szymon; Mynard, Frederic (2016). Convergence Foundations Of Topology. New Jersey: World Scientific Publishing Company. ISBN 978-981-4571-52-4. OCLC 945169917.
- Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
- Koutras, Costas D.; Moyzes, Christos; Nomikos, Christos; Tsaprounis, Konstantinos; Zikos, Yorgos (20 October 2021). "On Weak Filters and Ultrafilters: Set Theory From (and for) Knowledge Representation". Logic Journal of the IGPL. doi:10.1093/jigpal/jzab030.
- MacIver R., David (1 July 2004). "Filters in Analysis and Topology" (PDF). Archived from the original (PDF) on 2007-10-09. (Provides an introductory review of filters in topology and in metric spaces.)
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Willard, Stephen (2004) [1970]. General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
Further reading edit
- Bergman, George M.; Hrushovski, Ehud (1998). "Linear ultrafilters". Communications in Algebra. 26 (12): 4079–4113. CiteSeerX 10.1.1.54.9927. doi:10.1080/00927879808826396.