Blackboard bold is a style of writing bold symbols on a blackboard by doubling certain strokes, commonly used in mathematical lectures, and the derived style of typeface used in printed mathematical texts. The style is most commonly used to represent the number sets (natural numbers), (integers), (rational numbers), (real numbers), and (complex numbers).
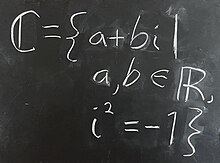
To imitate a bold typeface on a typewriter, a character can be typed over itself (called double-striking);[1] symbols thus produced are called double-struck, and this name is sometimes adopted for blackboard bold symbols,[2] for instance in Unicode glyph names.
In typography, a typeface with characters that are not solid is called inline, handtooled, or open face.[3]
History edit
Traditionally, various symbols were indicated by boldface in print but on blackboards and in manuscripts "by wavy underscoring, or enclosure in a circle, or even by wavy overscoring".[6]
Most typewriters have no dedicated bold characters at all. To produce a bold effect on a typewriter, a character can be double-struck with or without a small offset. By the mid 1960s typewriter accessories such as the "Doublebold" could automatically double-strike every character while engaged.[7] While this method makes a character bolder, and can effectively emphasize words or passages, in isolation a double-struck character is not always clearly different from its single-struck counterpart.[8][9]
Blackboard bold originated from the attempt to write bold symbols on typewriters and blackboards that were legible but distinct, perhaps starting in the late 1950s in France, and then taking hold at the Princeton University mathematics department in the early 1960s.[8][10] Mathematical authors began typing faux-bold letters by double-striking them with a significant offset or over-striking them with the letter I, creating new symbols such as IR, IN, CC, or ZZ; at the blackboard, lecturers began writing bold symbols with certain doubled strokes.[8][10] The notation caught on: blackboard bold spread from classroom to classroom and is now used around the world.[8]
The style made its way into print starting in the mid 1960s. Early examples include Robert Gunning and Hugo Rossi's Analytic Functions of Several Complex Variables (1965)[12][10] and Lynn Loomis and Shlomo Sternberg's Advanced Calculus (1968).[11] But initial adoption was sporadic and most publishers continued using boldface. In 1979 Wiley recommended its authors avoid "double-backed shadow or outline letters, sometimes called blackboard bold", because they could not always be printed;[13] in 1982 Wiley refused to include blackboard bold characters in mathematical books because the type was difficult and expensive to obtain.[14]
Donald Knuth preferred boldface to blackboard bold and so did not include blackboard bold in the Computer Modern typeface that he created for the TeX mathematical typesetting system he first released in 1978.[14] When Knuth's 1984 The TeXbook needed an example of blackboard bold for the index, he produced using the letters I and R with a negative space between;[15] in 1988 Robert Messer extended this to a full set of "poor person's blackboard bold" macros, overtyping each capital letter with carefully placed I characters or vertical lines.[16]
Not all mathematical authors were satisfied with such workarounds. The American Mathematical Society created a simple chalk-style blackboard bold typeface in 1985 to go with the AMS-TeX package created by Michael Spivak, accessed using the \Bbb command (for "blackboard bold"); a few years later in 1990, the AMS released an update with a new inline-style blackboard bold font intended to better match Times.[17] Since then, a variety of other blackboard bold typefaces have been created, some following the style of traditional inline typefaces and others closer in form to letters drawn with chalk.[18]
Unicode included the most common blackboard bold letters among the "Letterlike Symbols" in version 1.0 (1991), inherited from the Xerox Character Code Standard. Later versions of Unicode extended this set to all uppercase and lowercase Latin letters and a variety of other symbols, among the "Mathematical Alphanumeric Symbols".[19]
In professionally typeset books, publishers and authors have gradually adopted blackboard bold, and its use is now commonplace,[14] but some still use ordinary bold symbols. Some authors use blackboard bold letters on the blackboard or in manuscripts, but prefer an ordinary bold typeface in print; for example, Jean-Pierre Serre has used blackboard bold in lectures, but has consistently used ordinary bold for the same symbols in his published works.[20] The Chicago Manual of Style's recommendation has evolved over time: In 1993, for the 14th edition, it advised that "blackboard bold should be confined to the classroom" (13.14); In 2003, for the 15th edition, it stated that "open-faced (blackboard) symbols are reserved for familiar systems of numbers" (14.12). The international standard ISO 80000-2:2019 lists R as the symbol for the real numbers but notes "the symbols IR and are also used", and similarly for N, Z, Q, C, and P (prime numbers).[21]
Encoding edit
TeX, the standard typesetting system for mathematical texts, does not contain direct support for blackboard bold symbols, but the American Mathematical Society distributes the popular AMSFonts collection, loaded from the amssymb package, which includes a blackboard bold typeface for uppercase Latin letters accessed using \mathbb (e.g. \mathbb{R} produces ).[23]
In Unicode, a few of the more common blackboard bold characters (ℂ, ℍ, ℕ, ℙ, ℚ, ℝ, and ℤ) are encoded in the Basic Multilingual Plane (BMP) in the Letterlike Symbols (2100–214F) area, named DOUBLE-STRUCK CAPITAL C etc. The rest, however, are encoded outside the BMP, in Mathematical Alphanumeric Symbols (1D400–1D7FF), specifically from U+1D538 to U+1D550 (uppercase, excluding those encoded in the BMP), U+1D552 to U+1D56B (lowercase) and U+1D7D8 to U+1D7E1 (digits).
Usage edit
The following table shows all available Unicode blackboard bold characters.[24]
The first column shows the letter as typically rendered by the LaTeX markup system. The second column shows the Unicode code point. The third column shows the Unicode symbol itself (which will only display correctly on browsers that support Unicode and have access to a suitable typeface). The fourth column describes some typical usage in mathematical texts.[25] Some of the symbols (particularly and ) are nearly universal in their interpretation,[14] while others are more varied in use.
| LaTeX | Unicode code point (hex) | Unicode symbol | Mathematics usage |
|---|---|---|---|
U+1D538
|
𝔸 | Represents affine space, , or the ring of adeles. Occasionally represents the algebraic numbers,[26] the algebraic closure of (more commonly written or Q ), or the algebraic integers, an important subring of the algebraic numbers. | |
U+1D552
|
𝕒 | ||
U+1D539
|
𝔹 | Sometimes represents a ball, a boolean domain, or the Brauer group of a field. | |
U+1D553
|
𝕓 | ||
U+2102
|
ℂ | Represents the set of complex numbers.[14] | |
U+1D554
|
𝕔 | ||
U+1D53B
|
𝔻 | Represents the unit disk in the complex plane, for example as the conformal disk model of the hyperbolic plane. By generalisation may mean the n-dimensional ball. Occasionally may mean the decimal fractions (see number), split-complex numbers, or domain of discourse. | |
U+1D555
|
𝕕 | ||
U+2145
|
ⅅ | ||
U+2146
|
ⅆ | May represent the differential symbol. | |
U+1D53C
|
𝔼 | Represents the expected value of a random variable, or Euclidean space, or a field in a tower of fields, or the Eudoxus reals. | |
U+1D556
|
𝕖 | ||
U+2147
|
ⅇ | Occasionally used for the mathematical constant e. | |
U+1D53D
|
𝔽 | Represents a field.[26] Often used for finite fields, with a subscript to indicate the order.[26] Also represents a Hirzebruch surface or a free group, with a subscript to indicate the number of generators (or generating set, if infinite). | |
U+1D557
|
𝕗 | ||
U+1D53E
|
𝔾 | Represents a Grassmannian or a group, especially an algebraic group. | |
U+1D558
|
𝕘 | ||
U+210D
|
ℍ | Represents the quaternions (the H stands for Hamilton),[26] or the upper half-plane, or hyperbolic space,[26] or hyperhomology of a complex. | |
U+1D559
|
𝕙 | ||
U+1D540
|
𝕀 | The closed unit interval or the ideal of polynomials vanishing on a subset. Occasionally the identity mapping on an algebraic structure, or an indicator function. The set of imaginary numbers (i.e., the set of all real multiples of the imaginary unit). | |
U+1D55A
|
𝕚 | ||
U+2148
|
ⅈ | Occasionally used for the imaginary unit. | |
U+1D541
|
𝕁 | Sometimes represents the irrational numbers, . | |
U+1D55B
|
𝕛 | ||
U+2149
|
ⅉ | ||
U+1D542
|
𝕂 | Represents a field.[26] This is derived from the German word Körper, which is German for field (literally, 'body'; in French the term is corps). May also be used to denote a compact space. | |
U+1D55C
|
𝕜 | Represents a field. | |
U+1D543
|
𝕃 | Represents the Lefschetz motive. See Motive (algebraic geometry). | |
U+1D55D
|
𝕝 | ||
U+1D544
|
𝕄 | Sometimes represents the monster group. The set of all m-by-n matrices is sometimes denoted . In geometric algebra, represents the motor group of rigid motions. In functional programming and formal semantics, denotes the type constructor for a monad. | |
U+1D55E
|
𝕞 | ||
U+2115
|
ℕ | Represents the set of natural numbers.[21] May or may not include zero. | |
U+1D55F
|
𝕟 | ||
U+1D546
|
𝕆 | Represents the octonions.[26] | |
U+1D560
|
𝕠 | ||
U+2119
|
ℙ | Represents projective space, the probability of an event,[26] the prime numbers,[21] a power set, the positive reals, the irrational numbers, or a forcing poset. | |
U+1D561
|
𝕡 | ||
U+211A
|
ℚ | Represents the set of rational numbers.[14] (The Q stands for quotient.) | |
U+1D562
|
𝕢 | ||
U+211D
|
ℝ | Represents the set of real numbers.[14] | |
U+1D563
|
𝕣 | ||
U+1D54A
|
𝕊 | Represents a sphere, or the sphere spectrum, or occasionally the sedenions. | |
U+1D564
|
𝕤 | ||
U+1D54B
|
𝕋 | Represents the circle group, particularly the unit circle in the complex plane (and the n-dimensional torus), or a Hecke algebra (Hecke denoted his operators as Tn or ), or the tropical semiring, or twistor space. | |
U+1D565
|
𝕥 | ||
U+1D54C
|
𝕌 | ||
U+1D566
|
𝕦 | ||
U+1D54D
|
𝕍 | Represents a vector space or an affine variety generated by a set of polynomials, or in probability theory and statistics the variance. | |
U+1D567
|
𝕧 | ||
U+1D54E
|
𝕎 | Represents the whole numbers (here in the sense of non-negative integers), which also are represented by . | |
U+1D568
|
𝕨 | ||
U+1D54F
|
𝕏 | Occasionally used to denote an arbitrary metric space. | |
U+1D569
|
𝕩 | ||
U+1D550
|
𝕐 | ||
U+1D56A
|
𝕪 | ||
U+2124
|
ℤ | Represents the set of integers.[14] (The Z is for Zahlen, German for 'numbers', and zählen, German for 'to count'.) When it has a positive integer subscript, it can mean the finite cyclic group of that size. | |
U+1D56B
|
𝕫 | ||
U+213E
|
ℾ | ||
U+213D
|
ℽ | ||
U+213F
|
ℿ | ||
U+213C
|
ℼ | ||
U+2140
|
⅀ | ||
U+1D7D8
|
𝟘 | In algebra of logical propositions, it represents a contradiction or falsity. | |
U+1D7D9
|
𝟙 | In set theory, the top element of a forcing poset, or occasionally the identity matrix in a matrix ring. Also used for the indicator function and the unit step function, and for the identity operator or identity matrix. In geometric algebra, represents the unit antiscalar, the identity element under the geometric antiproduct. In algebra of logical propositions, it represents a tautology. | |
U+1D7DA
|
𝟚 | In category theory, the interval category. | |
U+1D7DB
|
𝟛 | ||
U+1D7DC
|
𝟜 | ||
U+1D7DD
|
𝟝 | ||
U+1D7DE
|
𝟞 | ||
U+1D7DF
|
𝟟 | ||
U+1D7E0
|
𝟠 | ||
U+1D7E1
|
𝟡 |
In addition, a blackboard-bold μn (not found in Unicode or amsmath LaTeX) is sometimes used by number theorists and algebraic geometers to designate the group scheme of n-th roots of unity.[27]
Note: Only uppercase Roman letters are given LaTeX renderings because Wikipedia's implementation uses the AMSFonts blackboard bold typeface, which does not support other characters.
See also edit
References edit
- ^ Gilreath, Charles T. (1993). "Graphic cueing of text: The typographic and diagraphic dimensions". Visible Language. 27 (3): 336–361.
- ^ Rosendorf, Theodore (2009). The Typographic Desk Reference. Oak Knoll Press. pp. 89–90.
- ^ Bringhurst, Robert (1992). "Glossary of Typographic Terms". Elements of Typographic Style. Hartley & Marks. p. 234. ISBN 0-88179-033-8.
Inline: A letter in which the inner portions of the main strokes have been carved away, leaving the edges more or less intact. Inline faces lighten the color while preserving the shapes and proportions of the original face.
Hutchings, R.S. (1965). "Inlines and Outlines". A Manual of Decorated Typefaces. Hastings House. pp. 10–11.Consuegra, David (2004). American Type: Design & Designers. Allworth Press. "Handtooled typefaces", p. 280; "Inline typefaces", p. 282; "Open face typefaces", p. 286–287.
- ^ Gunning, Robert C. (1966). Lectures on Riemann Surfaces. Mathematical Notes. Princeton University Press. p. 1.
- ^ Narasimhan, Raghavan (1966). Introduction to the Theory of Analytic Spaces. Lecture Notes in Mathematics. Vol. 25. Springer. p. 9. doi:10.1007/bfb0077071. ISBN 978-3-540-03608-1.
- ^ Hodgman, Charles D.; Selby, Samuel M.; Weast, Robert C., eds. (1959). C.R.C. Standard Mathematical Tables (12th ed.). Chemical Rubber Publishing Company. p. 494. Chaundy, Theodore W.; Barrett, P.R.; Batey, Charles (1954). The Printing of Mathematics. Oxford University Press. p. 52.
The sign for bold type is a wavy line beneath the words or symbols in question; for security the word 'bold' may be added in the margin.
- ^ Karch, R. Randolph (1970). Graphic Arts Procedures. American Technical Society. p. 199.
- ^ a b c d Webb, Stephen (2018). "Set of Natural Numbers ℕ". Clash Of Symbols: A Ride Through The Riches Of Glyphs. Springer. pp. 198–199, 233.
- ^ An example of double-struck type produced by an impact printer of the early 1980s can be found in: Waite, Mitchell; Arca, Julie (1982). Word Processing Primer. BYTE/McGraw-Hill. pp. 76–77.
- ^ a b c Rudolph, Lee (2003-10-06). "Re: History of blackboard bold?". Newsgroup: compt.text.tex. Archived from the original on 2021-09-23. Retrieved 2023-07-25. This usenet post (as mirrored by The Math Forum) seems to have been one of the sources for Webb 2018; see p. 233
- ^ a b Loomis, Lynn Harold; Sternberg, Shlomo (1968). Advanced Calculus. Addison Wesley. p. 241. The later revised edition is available from Sternberg's website.
- ^ Gunning, Robert C.; Rossi, Hugo (1965). Analytic functions of several complex variables. Prentice-Hall.
- ^ A guide for Wiley-Interscience and Ronald Press Authors in the Preparation and Production of Manuscript and Illustrations (2nd ed.). John Wiley & Sons. 1979.
- ^ a b c d e f g h Krantz, S. (2001). "2.8 Technical Issues". Handbook of Typography for the Mathematical Sciences. Chapman & Hall/CRC. p. 35. ISBN 9781584881490.
- ^ Knuth, Donald (1984). The TeXbook. Addison-Wesley. p. 460.
- ^ Messer, Robert (1988). "Blackboard Bold" (PDF). TUGboat. 9 (1): 19–20.
- ^ Beeton, Barbara (1985). "Mathematical Symbols and Cyrillic Fonts Ready for Distribution" (PDF). TUGboat. 6 (2): 59–63. Spivak, Michael (1986). The Joy of TeX: A Gourmet Guide to Typesetting with the AMS-TeX Macro Package. American Mathematical Society. p. 260. "Coming in January from the American Mathematical Society" (PDF). TUGboat. 10 (3): 365–366. 1989. Beeton, Barbara (2020-09-05). "Re: Who designed the mathematical blackboard bold letters of AMS, and when?". TeX–LaTeX Stack Exchange. Retrieved 2023-07-27.
The [1985] blackboard bold letters [...] are blocky in appearance, somewhat similar to those in the Monotype blackboard bold, but of much lower quality. (It's no surprise that Knuth did not like them.)
- ^ Vieth, Ulrik (2012). "OpenType math font development: Progress and challenges" (PDF). TUGboat. 33 (3): 302–308.
Design choices of Blackboard Bold alphabets again fall into multiple groups. One group favors a serif design which is derived from the main serif font: [...] Another group favor a sans-serif design which may be unrelated to the main sans-serif font: [...] Finally, the designs of individual letters can vary significantly among different math fonts, and are an additional consideration in font choice. For example, some users may have fairly strong preferences regarding such details as to whether the stem or the diagonal of the letter 'N' is double-struck.
- ^ Aliprand, Joan; Allen, Julie; et al., eds. (2003). "Math Alphanumeric Symbols: U+1D400–U+1D7FF". The Unicode Standard, Version 4.0. Addison-Wesley. pp. 354–357.
- ^ Example Serre lecture: "Writing Mathematics Badly" video talk (part 3/3), starting at 7′08″ Example Serre book: Serre, Jean-Pierre (1994). Cohomologie galoisienne. Springer.
- ^ a b c "7. Standard number sets and intervals". ISO 80000-2 Quantities and Units: Mathematics (2nd ed.). International Organization for Standardization. August 2019. Table 3, No. 2-7.4.
- ^ Kummer, Olaf (2006). "doublestroke – Typeset mathematical double stroke symbols". Comprehensive TeX Archive Network. Retrieved 2023-07-27.
- ^ Pakin, Scott (25 June 2020). The Comprehensive LATEX Symbol List (PDF). Archived (PDF) from the original on 2022-10-09.
- ^ Carlisle, David; Ion, Patrick (2023). "Double Struck (Open Face, Blackboard Bold)". XML Entity Definitions for Characters (Technical report) (3rd ed.). World Wide Web Consortium. Retrieved 2023-07-27.
Note: Characters highlighted [in yellow] are in the Plane 0 [Basic Multilingual Plane], not in the Mathematical Alphanumeric Symbols block in Plane 1.
- ^ Weisstein, Eric W. "Doublestruck". mathworld.wolfram.com. Retrieved 2022-12-21.
- ^ a b c d e f g h Sevryuk, Mikhail B. (1998-12-02). "Writing on a computer: some discouraging experiences". Arnold's Mathematical Seminar.
- ^ Milne, James S. (1980). Étale cohomology. Princeton University Press. pp. xiii, 66.




