User:Xelo747/sandbox

This is the user sandbox of Xelo747. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

Possible Bifurcations

Hopf Bifurcation

SNIC bifurcation

Homoclinic bifurcation

Current clamp simulations of the Morris-Lecar model. The injected current for the SNIC bifurcation and the homoclinic bifurcation is varied between 30 nA and 50 nA, while the current for the Hopf bifurcation is varied between 80nA and 100nA

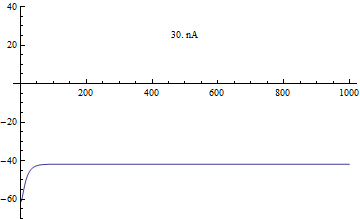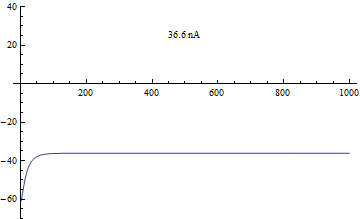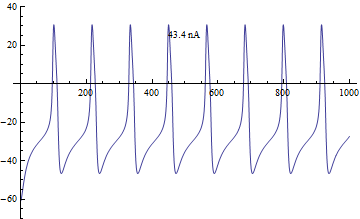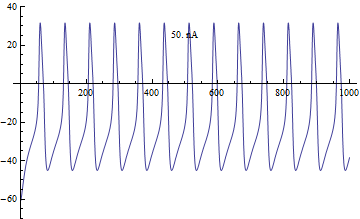
Kinetics edit

There are many different mathematical descriptions of ion channels but arguably the most accurate is the single channel kinetics using Markov Chains. An ion channel can exist in many different conductance states with transition rates governed by the voltage across the cell membrane.

Let us begin with a simple hypothetical Ion channel with two states, open $O$ and closed $C$ . The closed state transitions to the open state at a rate $\alpha (v)$ while the open state transitions to the closed state at rate $\beta (v)$ . Note that both $\alpha$ and $\beta$ are functions of voltage $v$ .

C{\overset {\alpha (v)}{\underset {\beta (v)}{\rightleftharpoons }}}O

Following Michaelis–Menten kinetics we can write down a formula for how a population of ion channels behave. Let $x={\frac {O}{O+C}}$ denote the percentage of ion channels in the open state. Similarly $1-x={\frac {C}{O+C}}$ is the percentage of ion channels in the closed state.

{\begin{aligned}{\frac {dx}{dt}}&=\alpha (v)x-\beta (v)((1-x)\\{\frac {dx}{dt}}&=(\alpha (v)+\beta (v))x-\beta (v)\\{\frac {dx}{dt}}&={\frac {x_{\infty }(v)-x}{\tau _{x}(v)}}\end{aligned}}

Conveniently $0<x_{\infty }(v)<1$ and $0<\tau _{x}(v)$ . $x_{\infty }(v)$ is known as the steady state and $\tau _{x}(v)$ is the time constant.

The most usual function for the stead state activation is usually a Boltzmann equation given by the form

x(V)={\frac {1}{2}}(1+\tanh({\frac {V-V_{\frac {1}{2}}}{k}}))

Random Equations edit

$C{\frac {dV}{dt}}=I_{inj}(t)-\sum _{i\in chan}g_{i}x_{i}^{p}y_{i}^{q}(V-E)$

${\frac {dx_{i}}{dt}}={\frac {x_{i_{\infty }}(V)-x_{i}}{\tau _{x_{i}}(V)}}$ hello ${\frac {dy_{i}}{dt}}={\frac {y_{i_{\infty }}(V)-y_{i}}{\tau _{y_{i}}(V)}}$ Pazuzu

$x_{i_{\infty }}(V)$ , $\tau _{x_{i}}(V)$ , $y_{i_{\infty }}(V)$ , $\tau _{y_{i}}(V)$ $I_{inj}(t)$