User:Tombo12354/sandbox

"Nose curve" redirects here. For a quartic curve, see Bullet-nose curve.

Normalized P-V curve

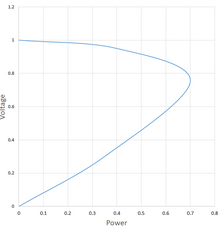
Power-voltage curve (also P-V curve) describes the relationship between the active power delivered to the electrical load and the voltage at the load terminals in an electric power system under a constant power factor. When plotted with power as a horizontal axis, the curve resembles a human nose, thus it is sometimes called a nose curve. The overall shape of the curve (similar to a parabola placed on its side) is defined by the power flow between two points connected by an impedance.

The curve is important for power system analysis, and helps define transient stability, or the ability of an AC system to recover from sudden disturbances. The tip of the "nose" defines the maximum power that can be delivered by the system, and can be adjusted by varying the parameters governing power flow. In general, a leading power factor stretches the nose further to the right and upwards, while a lagging power factor shrinks the curve.

Understanding the Power-Voltage relationship is an important part of understanding and control power flow. By changing the pv curve of a system, power transfer can be increased without adversly affecting voltage or stability.

Background

The PV curve, and more generally the power-voltage relationship, can be understood by analysis the power flow between two points connected through an impedance network. The two-port network model for a transmission line is often used for this, as it relates recieving-end voltage and current to the sending-end voltage and current and the transmission line parameters. It also allows the same analytical techniques for different types of lines, where different parameters dominate power transfer and voltage more. This model governs both the high-level relationship for power flow across a transmission line connecting two substations but also power out of a generator to its connection point.

Reviewing Impedance and Admittance is also important, as they are used and combined frequently. For reference, the impedance and admitance of resistors, inductors, and capacitors is included below.

Element	Impedance (Z)	Admittance (Y)
Resistor	${R}$	${\frac {1}{R}}$
Inductor	${j{\omega }L}$	${\frac {1}{j{\omega }L}}$
Capacitor	${\frac {1}{j{\omega }C}}$	$j{\omega }C$

Theory

Using the two-port model for a transmission line, the following equations represent sending-end voltage and current

${\bar {V_{s}}}={\bar {A}}{\bar {V_{r}}}+{\bar {B}}{\bar {I_{r}}}$

${\bar {I_{s}}}={\bar {C}}{\bar {V_{r}}}+{\bar {D}}{\bar {I_{r}}}$

where

${\bar {V_{s}}},{\bar {V_{r}}}$ are the voltage magnitude and phase-angle at the sending-end and recieving-end, respectively

${\bar {I_{s}}},{\bar {I_{r}}}$ are the current magnitude and phase-angle at the sending-end and recieving-end, respectively

${\bar {A}},{\bar {B}},{\bar {C}},{\bar {D}}$ are the ABCD parameters of the two-port model

The ABCD parameters and are shown as vectors, as they represent the impedance and admittance of the transmission line, and may have both magnitude and phase. Apparent Power, and thus real and reactive power, delivered to the recieving-end is given by

${\bar {S_{r}}}={\bar {V_{r}}}{\bar {I_{r}}}^{*}=P_{r}+jQ_{r}$

Combining this with the equation for sending-end voltage and simplifying gives

$P_{r}={\frac {V_{s}V_{r}}{B}}\cos {(\beta -\delta )}-{\frac {A{V_{r}}^{2}}{B}}\cos {(\beta -\alpha )}$

$Q_{r}={\frac {V_{s}V_{r}}{B}}\sin {(\beta -\delta )}-{\frac {A{V_{r}}^{2}}{B}}\sin {(\beta -\alpha )}$

Where $A,\alpha$ and $B,\beta$ represent the magnitude and phase-angle of ${\bar {A}}$ and ${\bar {B}}$, respectively, and $\delta$ is the phase-angle difference between the sending and recieving end voltages, referred to as the Power Angle, Torque Angle, or Load Angle. Examing the relation between recieving-end voltage and power shows the equation to be of the form $ry-sy^{2}=x$, which produces a sideways parabola, or the distinctive "nose" of the p-v curve.

These equations cover the general case of power flow, regardless of what assumption are use for the circuit parameters. Various cases can be used to analysis power under different applications.

Lossless Line

A special case where the transmission line consist of only a series inductance is often used to represent simple power transfer, and is referred to as the lossless transmission line. While not a real case, generally series inductance is far greater than series resistance, and shunt capacitance can actually improves power flow over just inductance. From this, the lossless transmission line offers a simple approximation that helps understand conceptual power flow.

With only a series inductance, the equations for sending-end voltage and current are

${\bar {V_{s}}}={\bar {V_{r}}}+{\bar {Z}}{\bar {I_{r}}}={\bar {V_{r}}}-jX_{L}{\bar {I_{r}}}$

${\bar {I_{s}}}={\bar {I_{r}}}={\bar {I}}$

from these equations, the ABCD matrix is

${\begin{bmatrix}1&jX_{L}\\0&1\end{bmatrix}}={\begin{bmatrix}1\angle 0&X_{L}\angle 90\\0\angle 0&1\angle 0\end{bmatrix}}$

using the identities $\cos(90-x)=\sin(x)$ and $\sin(90-x)=\cos(x)$, the real and reactive power simplify to

$P_{r}={\frac {V_{s}V_{r}}{X_{L}}}\sin(\delta )$

$Q_{r}={\frac {V_{r}}{X_{L}}}[V_{s}\cos(\delta )-V_{r}]$

Power delivered as a function of power angle shows that power transfer can be increased by increasing the power angle, maximizing at 90°. After that, further increases of power angle decrease power transfer. Plotting the voltage-power relationship of a lossless line shows them to be linearly related, where increasing voltage magnitude at the recieving end increases power transfer. While this implies a losslsss line could double the power flow by doubling the recieving-end voltage magnitude, realistically the recieving-end voltage cannot be increased much past its nominal rating without equipment failures. Normalizing the power and voltage by the per-unit base power and voltage, respectively, is common to make comparisons between systems easier.

Power can also be controlled by varying the voltage manitude at either end or changing the line impedance, however this requires more advanced devices, such as FACTs devices.

Short Transmission Line

The lossless model can be made more accurate by include a series resistance. This model is accurate represents shorter transmission lines, typically up to 50 miles. In short lines, shunt capacitance is negligible and typically not included.

With both a series resistance and inductance, the equations for sending-end voltage and current simplify are

${\bar {V_{s}}}={\bar {V_{r}}}+{\bar {Z}}{\bar {I_{r}}}={\bar {V_{r}}}+(R+jX_{L}){\bar {I_{r}}}$

${\bar {I_{s}}}={\bar {I_{r}}}={\bar {I}}$

from these equations, the ABCD matrix is

${\begin{bmatrix}1&R+jX_{L}\\0&1\end{bmatrix}}={\begin{bmatrix}1\angle 0&Z_{L}\angle \phi \\0\angle 0&1\angle 0\end{bmatrix}}$

where

$Z_{L}={\sqrt {R^{2}+X_{L}^{2}}}$ and is the magnitude of the lines impedance

$\phi =\arctan {({\frac {X_{L}}{R}})}$ and is the phase-angle between the resistance and reactance

Another common name for $\phi$ is the Power Factor angle, of which the Power Factor $pf=\cos {\phi }$. With these parameters, the real and reactive power become

$P_{r}={\frac {V_{s}V_{r}}{Z_{L}}}\cos {(\phi -\delta )}-{\frac {{V_{r}}^{2}}{Z_{L}}}\cos {(\phi )}$

$Q_{r}={\frac {V_{s}V_{r}}{Z_{L}}}\sin {(\phi -\delta )}-{\frac {{V_{r}}^{2}}{Z_{L}}}\sin {(\phi )}$

For $\phi =90$° $(R=0)$, the equation returns to the lossless case. With $\phi =0$° ($X=0$), there is no power transfer unless the sending-end magnitude is higher than the recieving end, and with a lower sending-end voltage negative power is transferred. While theoretically a concern, in reality the line's reactance is far greater than its resistance.

Medium Transmission Line

For transmission lines longer than 50 miles, the capacitance between the line and ground becomes significant. To accurately model these lines, the admittance of the transmission line needs to be considered, in addition to the line's impedance. The medium transmission line model is accurate for lines up to 150 miles.

While the transmission line's impedance is represented as a series resistance and inductance, it's admittance is represented as a shunt capacitance on either end of the impedance. With this model, commonly referred to as the Nominal $\Pi$ representation, three additional currents must be considered: the current in the sending-end admittance, the current through the line impedance, and the current in the recieving-end admittance. With these additional currents, the equations for recieving-end voltage and current become

${\bar {V_{s}}}={\bar {V_{r}}}+{\bar {Z}}{\bar {I_{Z}}}={\bar {V_{r}}}+{\bar {Z}}({\bar {I_{2}}}+{\bar {I_{r}}})$

${\bar {I_{s}}}={\bar {I_{Z}}}+{\bar {I_{2}}}=({\bar {I_{r}}}+{\bar {I_{1}}})+{\bar {I_{2}}}$

As the admittance is at the sending and recieving ends, the voltage across them is just the sending and recieving end voltages. Using ohms law, the equations can be rewritten

${\bar {V_{s}}}={\bar {V_{r}}}+{\bar {Z}}({\bar {I_{r}}}+{\frac {{\bar {Y}}{\bar {V_{r}}}}{2}})$

${\bar {I_{s}}}={\bar {I_{r}}}+{\frac {{\bar {V_{r}}}{\bar {Y}}}{2}}+{\frac {{\bar {V_{s}}}{\bar {Y}}}{2}}$

where

${\bar {Z}}=R+jX_{L}$

${\bar {Y}}=jX_{C}$

While the equation for sending-end voltage is in terms of recieving-end voltage and current, and provides the A and B parameters, the equation for sending-end current contains the sending-voltage. This can be manipulated by using the sending-end voltage equation to get an equation for the C and D parameters. From these equations, the ABCD matrix is

${\begin{bmatrix}{\frac {{\bar {Y}}{\bar {Z_{L}}}}{2}}+1&{\bar {Z_{L}}}\\{\bar {Y}}({\frac {{\bar {Y}}{\bar {Z_{L}}}}{4}}+1)&{\frac {{\bar {Y}}{\bar {Z_{L}}}}{2}}+1\end{bmatrix}}$

With these parameters, the real and reactive power become

$P_{r}={\frac {V_{s}V_{r}}{Z_{L}}}\cos {(\phi -\delta )}-{\frac {A{V_{r}}^{2}}{Z_{L}}}\cos {(\phi -\alpha )}$

$Q_{r}={\frac {V_{s}V_{r}}{Z_{L}}}\sin {(\phi -\delta )}-{\frac {A{V_{r}}^{2}}{Z_{L}}}\sin {(\phi -\alpha )}$

Where $A$ and $\alpha$ are the magnitude and phase angle of the A parameter.

Applications

Old

As the load increases from zero, the power-voltage point travels from the top left part of the curve to the tip of the "nose" (power increases, but the voltage drops). The tip corresponds to the maximum power that can be delivered to the load (as long as sufficient reactive power reserves are available). Past this "collapse" point additional loads cause drop in both voltage and power, as the power-voltage point travels to the bottom left corner of the plot. Intuitively this result can be explained when a load that consists entirely of resistors is considered: as the load increases (its resistance thus lowers), more and more of the generator power dissipates inside the generator itself (that has it own fixed resistance connected sequentially with the load). Operation on the bottom part of the curve (where the same power is delivered with lower voltage – and thus higher current and losses) is not practical, as it corresponds to the "uncontrollability" region.

If sufficient reactive power is not available, the limit of the load power will be reached prior to the power-voltage point getting to the tip of the "nose". The operator shall maintain a sufficient margin between the operating point on the P-V curve and this maximum loading condition, otherwise, a voltage collapse can occur.

A similar curve for the reactive power is called Q-V curve.

Sources

• Van Cutsem, Thierry; Vournas, Costas (2006). "Emergency Monitoring and Corrective Control of Voltage Instability: PV Curves and Maximum Load Power". Real-Time Stability in Power Systems: Techniques for Early Detection of the Risk of Blackout. Springer Science & Business Media. pp. 95-. ISBN 978-0-387-25626-9. OCLC 1039231417.
• Padiyar, K. R.; Kulkarni, Anil M. (31 December 2018). Dynamics and Control of Electric Transmission and Microgrids. John Wiley & Sons. p. 286. ISBN 978-1-119-17339-7. OCLC 1048018159.
• Machowski, Jan; Bialek, Janusz W.; Bumby, Jim (31 August 2011). Power System Dynamics: Stability and Control (2 ed.). John Wiley & Sons. ISBN 978-1-119-96505-3. OCLC 1037459298.
• Milano, Federico (8 September 2010). Power System Modelling and Scripting. Springer Science & Business Media. p. 106. ISBN 978-3-642-13669-6. OCLC 1005815809.
• Tang, Yong (7 April 2021). Voltage Stability Analysis of Power System. Springer Nature. pp. 32–33. ISBN 978-981-16-1071-4. OCLC 1246238334.