User:Harry Princeton/Uniform tilings

Summary

1-uniform tilings include 3 regular tilings, and 8 semiregular ones, with 2 or more types of regular polygon faces. There are 20 2-uniform tilings. 3-uniform tilings include 22 2-Catalaves tilings and 39 3-Catalaves ones. The 3 regular tilings have regular dual tilings. In general n-isogonal tilings have n-isohedral dual tilings, with 1-to-1 correspondence between vertices of $n$ uniform tilings and the planigons of dual $n$ uniform tilings.

k-uniform, m-Archimedean tiling counts

	m
	1	2	3	4	5	6	7	14	15	Total
1	11	0	0	0	0	0	0	0	0	11
2	0	20	0	0	0	0	0	0	0	22
3	0	22	39	0	0	0	0	0	0	61
4	0	33	85	33	0	0	0	0	0	151
5	0	74	149	94	15	0	0	0	0	332
6	0	100	284	187	92	10	0	0	0	673
7	?	?	?	?	?	?	7	0	0	a lot
14	?	?	?	?	?	?	?	0	0	∞
15	0	0	0	0	0	0	0	0	0	0

For example, these are two 14-Catalaves tilings, one with 92 uniformity (mine), and the other with 174 uniformity:

Two 14-Catalaves Tilings

O34S12T6EI2Rr11D14F3s2C9B23H3	O438S8T4EI2Rr13D12F2s2C88B19H10
$1+4+12+6+1+2+1+11+14+3+2+9+23+3=92$	$4+8+8+4+1+2+1+13+12+2+2+88+19+10=174$

Dual Polygonal Faces (Coregular Polygons or Vertex Regular Planigons)

OSTEIRrDFsCBHi (fifteen VRPs)

There are 15 vertex regular planigons (VRPs) in dual uniform tilings, 14 of which can be present in dual $k\geq 2$ uniform tilings:

1. Isosceles obtuse triangle (V3.12²): O.
2. 30-60-90 right triangle (V4.6.12): 3.
3. Skew quadrilateral (V3².4.12): S.
4. Tie kite (V3.4.3.12): T.
5. Equilateral triangle (V6³): E.
6. Isosceles trapezoid (V3².6²): I.
7. Rhombus (V(3.6)²): R.
8. Right trapezoid (V3.4².6): r.
9. Deltoid (V3.4.6.4): D.
10. Floret pentagon (V3⁴.6): F.
11. Square (V4⁴): s.
12. Cairo pentagon (V3².4.3.4): C.
13. Barn pentagon (V3³.4²): B.
14. Hexagon (V3⁶): H.
15. Isosceles right triangle (V4.8²): i.

or O3STEIRrDFsCBHi for short. Note that i stands by itself in the kisquadrille tiling. They are presented below:

Triangles				Quadrilaterals
V4.82	V3.122	V4.6.12	V63	V32.4.12	V3.4.3.12	V32.62	V(3.6)2
	Quadrilaterals			Pentagons			Hexagon
	V3.42.6	V3.4.6.4	V44	V34.6	V32.4.3.4	V33.42	V36

The square tiling (Q) is self-dual, so that s = V4⁴ is a square, and the triangular tiling E (Δ) and hexagonal tiling H (H) are dual to each other.

Everything except for STIr can tile the plane alone (the 3 regular and 8 Laves tilings).

For STIr, four dual 2-uniform tilings using S, T, I, r in the highest proportion are shown, in addition to a 7-Krötenheerdt dual uniform tiling 3STIrCB which uses all four:

Four demiregular planigons ('semiplanigons') to scale, plus one with all four.

Quadrilaterals				All
SH	OT	IH	Rr	3STIrCB
				(all)

Derivation of Demiregular VRPs (STIr)

3 demiregular VRPs can also be derived by adding or removing tiny triangles from 3 of the 11 Catalaves VRPs: the skew quadrilateral V(3².4.12) is a truncated scalene right triangle V(4.6.12). The isosceles trapezoid is a truncated triangle V(6³) or extended Floret pentagon V(3⁴.6). The right trapezoid V(3.4².6) is an extended prismatic pentagon V(3³.4²). Meanwhile, the last demiregular VRP, the tie kite V(3.4.3.12), can be derived by dissecting a square V(4⁴) into four equilateral triangles V(6³) and four tie kites V(3.4.3.12), but not to scale!

3 demiregular VRPs can also be derived by adding or removing tiny triangles from 3 of the 11 Catalaves VRPs: the skew quadrilateral V(3².4.12) is a truncated scalene right triangle V(4.6.12). The isosceles trapezoid is a truncated triangle V(6³) or extended Floret pentagon V(3⁴.6). The right trapezoid V(3.4².6) is an extended prismatic pentagon V(3³.4²). Meanwhile, the last demiregular VRP, the tie kite V(3.4.3.12), can be derived by dissecting a square V(4⁴) into four equilateral triangles V(6³) and four tie kites V(3.4.3.12), but not to scale!

A Cutlery of Planigons

All vertex regular planigons are shown to scale, in sufficiently many orientations. Every planigon in all 12 or 24 orientations realized, such that the reference side length of the uniform tilings is 201 pixels.

All vertex regular planigons colored by number of sides. So triangles are colored yellow, quadrilaterals red, pentagons cyan, and hexagons green. This is consistent with uniform tilings, and may be confused as such. There is little variety here.

A collection of all usable regular polygons and vertex regular planigons, in dark version. This can be used in MS Paint (with flips and 90-degree rotations) to create arbitrary convex uniform and dual uniform tilings, colored by vertex regular planigon (for uniformity, shade them different colors). The pixel size is 104 pixels per unit.

Every planigon in all 12 or 24 orientations realized, such that the reference side length of the uniform tilings is 104 pixels. Made in Paint.

Every planigon in all 12 or 24 orientations realized, such that the reference side length of the uniform tilings is 104 pixels. The sides of all planigons are uniformized, such that every pair of edges coincides without pixel overlap. In fact, this also includes the two generalized (multi-tiled) insets, one over degree six vertices and one over degree twelve vertices.

A basis of regular polygons, planigons, and semiplanigons which are used to cover k-dual uniform tilings. There are 15 polygons in all. All the sides are uniformized, and everything is to scale. The side length reads $s=2{\sqrt {3}}$.

The dual construction of all planigons, colored and transparent. The center of every regular polygon face is connected at the midpoints to form the planigons. A better version is shown below, in the construction of the fifteen VRPs:

Miscellaneous: a Project in Uniform Planar Tilings

Listed on top are 65 of Tomruen's k-uniform tilings. Then it is transformed into Harry Princeton's version, along with the dual uniform tilings, to scale and adequately colored. Faint dissections/insets are shown whenever applicable. Scroll for convenience.

A project in uniform planar tilings by Harry Princeton.

OSTEIRrDFsCBHi (fifteen VRPs)

O3STEIRrDFsCBHi for short:

i	O	3	E	S	T	I	R
	r	D	s	F	C	B	H

The Regular (Dual) Tilings

Again, the square tiling (Q) is self-dual, so that s = V4⁴ is a square, and the triangular tiling E (Δ) and hexagonal tiling H (H) are dual to each other.

3 Regular dual tilings

E	s	H

The Laves Tilings

There are 8 semiregular Laves Tilings:

8 Semiregular Laves Tilings

Triangles
i	O	3
Quadrilaterals
R	D
Pentagons
F	C	B

20 Dual 2-Uniform Tilings

There are 20 2-dual uniform tilings. They can only be Krötenheerdt (2-uniform, 2-Catalaves):

20 Duals of 2-uniform (demiregular) tilings (all Krötenheerdt)

CH	DC	DB	rD	3D
SH	OT	IH	FH	FH2
IF	IR	Rr	Rr2	CB
CB2	sB	sB2	BH	BH2

Side-by-side comparison of uniform and co-uniform tilings

Main article: List of k-uniform tilings

Side-by-side comparison of uniform and co-uniform tilings from List of k-uniform tilings:

Uniform						Co-uniform

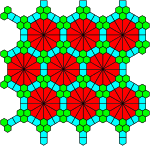
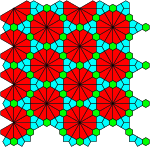
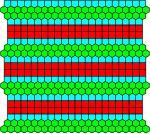
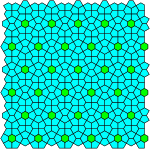
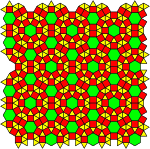
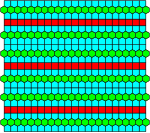
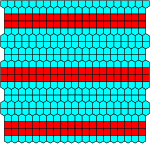
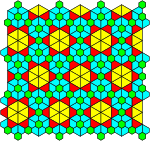
References

• Grunbaum, Branko; Shephard, Geoffrey C. (1977). "Tilings by regular polygons". Math. Mag. 50 (5): 227–247. doi:10.2307/2689529. JSTOR 2689529.
• Grünbaum, Branko; Shephard, G. C. (1978). "The ninety-one types of isogonal tilings in the plane". Trans. Am. Math. Soc. 252: 335–353. doi:10.1090/S0002-9947-1978-0496813-3. MR 0496813.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Debroey, I.; Landuyt, F. (1981). "Equitransitive edge-to-edge tilings". Geometriae Dedicata. 11 (1): 47–60. doi:10.1007/BF00183189.
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Ren, Ding; Reay, John R. (1987). "The boundary characteristic and Pick's theorem in the Archimedean planar tilings". J. Combinat. Theory A. 44 (1): 110–119. doi:10.1016/0097-3165(87)90063-X.
• Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
• Order in Space: A design source book, Keith Critchlow, 1970 ISBN 978-0-670-52830-1
• Sommerville, Duncan MacLaren Young (1958). An Introduction to the Geometry of n Dimensions. Dover Publications. Chapter X: The Regular Polytopes
• Préa, P. (1997). "Distance sequences and percolation thresholds in Archimedean Tilings". Mathl. Comput. Modelling. 26 (8–10): 317–320. doi:10.1016/S0895-7177(97)00216-1.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Kovic, Jurij (2011). "Symmetry-type graphs of Platonic and Archimedean solids". Math. Commun. 16 (2): 491–507.
• Pellicer, Daniel; Williams, Gordon (2012). "Minimal covers of the Archimedean Tilings". El. J. Combinat. 19 (3): #P6. doi:10.37236/2512.

External links

• n-uniform tilings Brian Galebach
• Dutch, Steve. "Uniform Tilings". Retrieved 2006-09-09.
• Weisstein, Eric W. "Tessellation". MathWorld.
• Weisstein, Eric W. "Semiregular tessellation". MathWorld.
• Weisstein, Eric W. "Demiregular tessellation". MathWorld.