User:Camiloortizas/Sandbox

Gaussian q-distribution

The Gaussian $q$-distribution introduced by Diaz and Teruel is a q-analogue of the Gaussian or Normal distribution.

Let $q$ be a real number in the interval [0,1). The Gaussian $q$-density is the function

$s_{q}:\mathbb {R} \rightarrow \mathbb {R}$

given by

$s_{q}={\begin{cases}0&{\mbox{if }}x<-\nu \\{\frac {1}{c(q)}}E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]_{q}}}&{\mbox{if }}-\nu \leq x\leq \nu \\0&{\mbox{if }}x>\nu .\end{cases}}$

where

$\nu =\nu (q)={\frac {1}{\sqrt {1-q}}}$

$c(q)=2(1-q)^{1/2}\sum _{m=0}^{\infty }{\frac {(-1)^{m}q^{(m)(m+1)}}{(1-q^{2m+1})(1-q^{2})_{q^{2}}^{m}}}$.

The $q$-analogue $[t]_{q}$ of the real number $t$ is given by

$[t]_{q}={\frac {q^{t}-1}{q-1}}$.

The $q$-analogue of the exponential function $E_{q}^{x}$ is given by

$E_{q}^{x}=\sum _{j=0}^{\infty }q^{j(j-1)/2}{\frac {x^{j}}{[j]!}}$

where the $q$-analogue of the factorial $[n]_{q}!$ is given by

$[n]_{q}!=[n]_{q}[n-1]_{q}...[2]_{q}$

for an integer $n>2$ and $[1]_{q}!=[0]_{q}!=1$

The cumulative Gaussian $q$-distribution

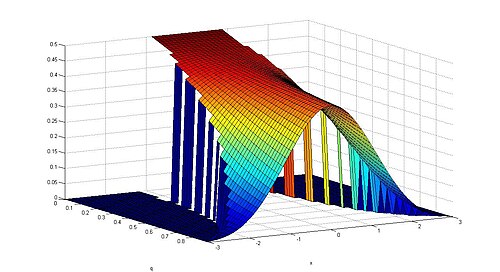The Gaussian q-density.

$G_{q}:\mathbb {R} \rightarrow \mathbb {R}$

is given by

${\begin{cases}0&{\mbox{if }}x<-\nu \\{\frac {1}{c(q)}}\int _{-\nu }^{x}E_{q^{2}}^{\frac {-q^{2}t^{2}}{[2]}}d_{q}t&{\mbox{if }}-\nu \leq x\leq \nu \\1&{\mbox{if }}x>\nu \end{cases}}$

where the integration symbol denotes the Jackson integral.

Explicitly the function $G_{q}$ is given by

$G_{q}(x)={\begin{cases}0&{\mbox{if}}x<-\nu ,\\{\displaystyle {\frac {1}{2}}+{\frac {1-q}{c(q)}}\sum _{n=0}^{\infty }{\frac {q^{n(n+1)}(q-1)^{n}}{(1-q^{2n+1})(1-q^{2})_{q^{2}}^{n}}}x^{2n+1}}&{\mbox{if }}-\nu \leq x\leq \nu \\1&{\mbox{if}}\ x>\nu \end{cases}}$

where $(a+b)_{q}^{n}=\prod _{i=0}^{n-1}(a+q^{i}b)$

The Cumulative Gaussian q-distribution.

The moment (mathematics) of the Gaussian $q$-distribution are given by

${\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]}}x^{2n}d_{q}x=[2n-1]!!$

${\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]}}x^{2n+1}d_{q}x=0$

Where the symbol $[2n-1]!!$
is the q-analogue of the double factorial given by

$[2n-1][2n-3]\cdots [1]=[2n-1]!!$

References

• R. Diaz, E. Pariguan, On the Gaussian q-distribution, J. Math. Anal. Appl. 358 (2009) 1-9.

• R. Diaz, C. Teruel, q,k-Generalized Gamma and Beta Functions, J. Nonlinear Math. Phys. 12 (2005) 118–134.