The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data.[1] System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences (inputs to the system) and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
| Black box systems | |
|---|---|
 | |
| System | |
| Black box, Oracle machine | |
| Methods and techniques | |
| Black-box testing, Blackboxing | |
| Related techniques | |
| Feed forward, Obfuscation, Pattern recognition, White box, White-box testing, Gray-box testing, System identification | |
| Fundamentals | |
| A priori information, Control systems, Open systems, Operations research, Thermodynamic systems | |
Overview
editA dynamic mathematical model in this context is a mathematical description of the dynamic behavior of a system or process in either the time or frequency domain. Examples include:
- physical processes such as the movement of a falling body under the influence of gravity;
- economic processes such as stock markets that react to external influences.
One of the many possible applications of system identification is in control systems. For example, it is the basis for modern data-driven control systems, in which concepts of system identification are integrated into the controller design, and lay the foundations for formal controller optimality proofs.
Input-output vs output-only
editSystem identification techniques can utilize both input and output data (e.g. eigensystem realization algorithm) or can include only the output data (e.g. frequency domain decomposition). Typically an input-output technique would be more accurate, but the input data is not always available.
Optimal design of experiments
editThe quality of system identification depends on the quality of the inputs, which are under the control of the systems engineer. Therefore, systems engineers have long used the principles of the design of experiments.[2] In recent decades, engineers have increasingly used the theory of optimal experimental design to specify inputs that yield maximally precise estimators.[3][4]
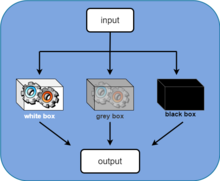
White- and black-box
editOne could build a white-box model based on first principles, e.g. a model for a physical process from the Newton equations, but in many cases, such models will be overly complex and possibly even impossible to obtain in reasonable time due to the complex nature of many systems and processes.
A more common approach is therefore to start from measurements of the behavior of the system and the external influences (inputs to the system) and try to determine a mathematical relation between them without going into the details of what is actually happening inside the system. This approach is called system identification. Two types of models are common in the field of system identification:
- grey box model: although the peculiarities of what is going on inside the system are not entirely known, a certain model based on both insight into the system and experimental data is constructed. This model does however still have a number of unknown free parameters which can be estimated using system identification.[5][6] One example[7] uses the Monod saturation model for microbial growth. The model contains a simple hyperbolic relationship between substrate concentration and growth rate, but this can be justified by molecules binding to a substrate without going into detail on the types of molecules or types of binding. Grey box modeling is also known as semi-physical modeling.[8]
- black box model: No prior model is available. Most system identification algorithms are of this type.
In the context of nonlinear system identification Jin et al.[9] describe grey-box modeling by assuming a model structure a priori and then estimating the model parameters. Parameter estimation is relatively easy if the model form is known but this is rarely the case. Alternatively, the structure or model terms for both linear and highly complex nonlinear models can be identified using NARMAX methods.[10] This approach is completely flexible and can be used with grey box models where the algorithms are primed with the known terms, or with completely black-box models where the model terms are selected as part of the identification procedure. Another advantage of this approach is that the algorithms will just select linear terms if the system under study is linear, and nonlinear terms if the system is nonlinear, which allows a great deal of flexibility in the identification.
Identification for control
editIn control systems applications, the objective of engineers is to obtain a good performance of the closed-loop system, which is the one comprising the physical system, the feedback loop and the controller. This performance is typically achieved by designing the control law relying on a model of the system, which needs to be identified starting from experimental data. If the model identification procedure is aimed at control purposes, what really matters is not to obtain the best possible model that fits the data, as in the classical system identification approach, but to obtain a model satisfying enough for the closed-loop performance. This more recent approach is called identification for control, or I4C in short.
The idea behind I4C can be better understood by considering the following simple example.[11] Consider a system with true transfer function :
and an identified model :
From a classical system identification perspective, is not, in general, a good model for . In fact, modulus and phase of are different from those of at low frequency. What is more, while is an asymptotically stable system, is a simply stable system. However, may still be a model good enough for control purposes. In fact, if one wants to apply a purely proportional negative feedback controller with high gain , the closed-loop transfer function from the reference to the output is, for
and for
Since is very large, one has that . Thus, the two closed-loop transfer functions are indistinguishable. In conclusion, is a perfectly acceptable identified model for the true system if such feedback control law has to be applied. Whether or not a model is appropriate for control design depends not only on the plant/model mismatch but also on the controller that will be implemented. As such, in the I4C framework, given a control performance objective, the control engineer has to design the identification phase in such a way that the performance achieved by the model-based controller on the true system is as high as possible.
Sometimes, it is even more convenient to design a controller without explicitly identifying a model of the system, but directly working on experimental data. This is the case of direct data-driven control systems.
Forward model
editA common understanding in Artificial Intelligence is that the controller has to generate the next move for a robot. For example, the robot starts in the maze and then the robot decides to move forward. Model predictive control determines the next action indirectly. The term “model” is referencing to a forward model which doesn't provide the correct action but simulates a scenario.[12] A forward model is equal to a physics engine used in game programming. The model takes an input and calculates the future state of the system.
The reason why dedicated forward models are constructed is because it allows one to divide the overall control process. The first question is how to predict the future states of the system. That means, to simulate a plant over a timespan for different input values. And the second task is to search for a sequence of input values which brings the plant into a goal state. This is called predictive control.
The forward model is the most important aspect of a MPC-controller. It has to be created before the solver can be realized. If it's unclear what the behavior of a system is, it's not possible to search for meaningful actions. The workflow for creating a forward model is called system identification. The idea is to formalize a system in a set of equations which will behave like the original system.[13] The error between the real system and the forward model can be measured.
There are many techniques available to create a forward model: ordinary differential equations is the classical one which is used in physics engines like Box2d. A more recent technique is a neural network for creating the forward model.[14]
See also
edit- Black box
- Generalized filtering
- Hysteresis
- Structural identifiability
- System realization
- Parameter estimation
- Linear time-invariant system theory
- Model selection
- Nonlinear autoregressive exogenous model
- Open system (systems theory)
- Pattern recognition
- System dynamics
- Systems theory
- Model order reduction
- Grey box completion and validation
- Data-driven control system
- Black box model of power converter
References
edit- ^ Torsten, Söderström; Stoica, P. (1989). System identification. New York: Prentice Hall. ISBN 978-0138812362. OCLC 16983523.
- ^ Spall, J. C. (2010), “Factorial Design for Efficient Experimentation: Generating Informative Data for System Identification,” IEEE Control Systems Magazine, vol. 30(5), pp. 38–53. https://doi.org/10.1109/MCS.2010.937677
- ^ Goodwin, Graham C. & Payne, Robert L. (1977). Dynamic System Identification: Experiment Design and Data Analysis. Academic Press. ISBN 978-0-12-289750-4.
- ^ Walter, Éric & Pronzato, Luc (1997). Identification of Parametric Models from Experimental Data. Springer.
- ^ Nielsen, Henrik Aalborg; Madsen, Henrik (December 2000). "Predicting the Heat Consumption in District Heating Systems using Meteorological Forecasts" (PDF). Lyngby: Department of Mathematical Modelling, Technical University of Denmark. S2CID 134091581. Archived from the original (PDF) on 2017-04-21.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Nielsen, Henrik Aalborg; Madsen, Henrik (January 2006). "Modelling the heat consumption in district heating systems using a grey-box approach". Energy and Buildings. 38 (1): 63–71. doi:10.1016/j.enbuild.2005.05.002. ISSN 0378-7788.
- ^ Wimpenny, J.W.T. (April 1997). "The Validity of Models". Advances in Dental Research. 11 (1): 150–159. doi:10.1177/08959374970110010601. ISSN 0895-9374. PMID 9524451. S2CID 23008333.
- ^ Forssell, U.; Lindskog, P. (July 1997). "Combining Semi-Physical and Neural Network Modeling: An Example of Its Usefulness". IFAC Proceedings Volumes. 30 (11): 767–770. doi:10.1016/s1474-6670(17)42938-7. ISSN 1474-6670.
- ^ Gang Jin; Sain, M.K.; Pham, K.D.; Billie, F.S.; Ramallo, J.C. (2001). "Modeling MR-dampers: A nonlinear blackbox approach". Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148). IEEE. pp. 429-434 vol.1. doi:10.1109/acc.2001.945582. ISBN 978-0780364950. S2CID 62730770.
- ^ Billings, Stephen A (2013-07-23). Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio–Temporal Domains. doi:10.1002/9781118535561. ISBN 9781118535561.
- ^ Gevers, Michel (January 2005). "Identification for Control: From the Early Achievements to the Revival of Experiment Design*". European Journal of Control. 11 (4–5): 335–352. doi:10.3166/ejc.11.335-352. ISSN 0947-3580. S2CID 13054338.
- ^ Nguyen-Tuong, Duy and Peters, Jan (2011). "Model learning for robot control: a survey". Cognitive Processing. 12 (4). Springer: 319–340. doi:10.1007/s10339-011-0404-1. PMID 21487784. S2CID 8660085.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Kopicki, Marek and Zurek, Sebastian and Stolkin, Rustam and Moerwald, Thomas and Wyatt, Jeremy L (2017). "Learning modular and transferable forward models of the motions of push manipulated objects". Autonomous Robots. 41 (5). Springer: 1061–1082. doi:10.1007/s10514-016-9571-3.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Eric Wan and Antonio Baptista and Magnus Carlsson and Richard Kiebutz and Yinglong Zhang and Alexander Bogdanov (2001). Model predictive neural control of a high-fidelity helicopter model. {AIAA. American Institute of Aeronautics and Astronautics. doi:10.2514/6.2001-4164.
Further reading
edit- Goodwin, Graham C. & Payne, Robert L. (1977). Dynamic System Identification: Experiment Design and Data Analysis. Academic Press.
- Daniel Graupe: Identification of Systems, Van Nostrand Reinhold, New York, 1972 (2nd ed., Krieger Publ. Co., Malabar, FL, 1976)
- Eykhoff, Pieter: System Identification – Parameter and System Estimation, John Wiley & Sons, New York, 1974. ISBN 0-471-24980-7
- Lennart Ljung: System Identification — Theory For the User, 2nd ed, PTR Prentice Hall, Upper Saddle River, N.J., 1999.
- Jer-Nan Juang: Applied System Identification, Prentice-Hall, Upper Saddle River, N.J., 1994.
- Kushner, Harold J. and Yin, G. George (2003). Stochastic Approximation and Recursive Algorithms and Applications (Second ed.). Springer.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Oliver Nelles: Nonlinear System Identification, Springer, 2001. ISBN 3-540-67369-5
- T. Söderström, P. Stoica, System Identification, Prentice Hall, Upper Saddle River, N.J., 1989. ISBN 0-13-881236-5
- R. Pintelon, J. Schoukens, System Identification: A Frequency Domain Approach, 2nd Edition, IEEE Press, Wiley, New York, 2012. ISBN 978-0-470-64037-1
- Spall, J. C. (2003), Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control, Wiley, Hoboken, NJ.
- Walter, Éric & Pronzato, Luc (1997). Identification of Parametric Models from Experimental Data. Springer.