In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter H, is a distance (vertical or radial) over which a physical quantity decreases by a factor of e (the base of natural logarithms, approximately 2.718).
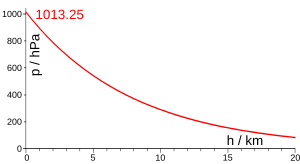
Scale height used in a simple atmospheric pressure model edit
For planetary atmospheres, scale height is the increase in altitude for which the atmospheric pressure decreases by a factor of e. The scale height remains constant for a particular temperature. It can be calculated by[1][2]
- kB = Boltzmann constant = 1.381×10−23 J⋅K−1[3]
- R = gas constant
- T = mean atmospheric temperature in kelvins = 250 K[4] for Earth
- m = mean mass of a molecule (units kg)
- M = mean mass of one mol of atmospheric particles = 0.029 kg/mol for Earth
- g = acceleration due to gravity at the current location (m/s2)
The pressure (force per unit area) at a given altitude is a result of the weight of the overlying atmosphere. If at a height of z the atmosphere has density ρ and pressure P, then moving upwards an infinitesimally small height dz will decrease the pressure by amount dP, equal to the weight of a layer of atmosphere of thickness dz.
Thus:
Combining these equations gives
This translates as the pressure decreasing exponentially with height.[5]
In Earth's atmosphere, the pressure at sea level P0 averages about 1.01×105 Pa, the mean molecular mass of dry air is 28.964 u and hence m = 28.964 × 1.660×10−27 = 4.808×10−26 kg. As a function of temperature, the scale height of Earth's atmosphere is therefore H/T = k/mg = (1.38/(4.808×9.81))×103 = 29.26 m/K. This yields the following scale heights for representative air temperatures.
- T = 290 K, H = 8500 m
- T = 273 K, H = 8000 m
- T = 260 K, H = 7610 m
- T = 210 K, H = 6000 m
These figures should be compared with the temperature and density of Earth's atmosphere plotted at NRLMSISE-00, which shows the air density dropping from 1200 g/m3 at sea level to 0.53 = 0.125 g/m3 at 70 km, a factor of 9600, indicating an average scale height of 70/ln(9600) = 7.64 km, consistent with the indicated average air temperature over that range of close to 260 K.
Note:
- Density is related to pressure by the ideal gas laws. Therefore, density will also decrease exponentially with height from a sea level value of ρ0 roughly equal to 1.2 kg m−3
- At heights over 100 km, an atmosphere may no longer be well mixed. Then each chemical species has its own scale height.
- Here temperature and gravitational acceleration were assumed to be constant but both may vary over large distances.
Planetary examples edit
Approximate atmospheric scale heights for selected Solar System bodies follow.
Scale height for a thin disk edit
For a disk of gas around a condensed central object, such as, for example, a protostar, one can derive a disk scale height which is somewhat analogous to the planetary scale height. We start with a disc of gas that has a mass which is small relative to the central object. We assume that the disc is in hydrostatic equilibrium with the z component of gravity from the star, where the gravity component is pointing to the midplane of the disk:
where:
- G = Gravitational constant ≈ 6.674×10−11 m3⋅kg−1⋅s−2[15]
- r = the radial cylindrical coordinate for the distance from the center of the star or centrally condensed object
- z = the height/altitude cylindrical coordinate for the distance from the disk midplane (or center of the star)
- M* = the mass of the star/centrally condensed object
- P = the pressure of the gas in the disk
- = the gas mass density in the disk
In the thin disk approximation, and the hydrostatic equilibrium equation is
To determine the gas pressure, one can use the ideal gas law:
- T = the gas temperature in the disk, where the temperature is a function of r, but independent of z
- = the mean molecular mass of the gas
Using the ideal gas law and the hydrostatic equilibrium equation, gives:
As an illustrative approximation, if we ignore the radial variation in the temperature, , we see that and that the disk increases in altitude as one moves radially away from the central object.
Due to the assumption that the gas temperature in the disk, T, is independent of z, is sometimes known as the isothermal disk scale height.
Disk scale height in a magnetic field edit
A magnetic field in a thin gas disk around a central object can change the scale height of the disk.[16][17][18] For example, if a non-perfectly conducting disk is rotating through a poloidal magnetic field (i.e., the initial magnetic field is perpendicular to the plane of the disk), then a toroidal (i.e., parallel to the disk plane) magnetic field will be produced within the disk, which will pinch and compress the disk. In this case, the gas density of the disk is:[18]
- is the permeability of free space
- is the electrical conductivity of the disk
- is the magnetic flux density of the poloidal field in the direction
- is the rotational angular velocity of the central object (if the poloidal magnetic field is independent of the central object then can be set to zero)
- is the keplerian angular velocity of the disk at a distance from the central object.
These formulae give the maximum height, , of the magnetized disk as
See also edit
References edit
- ^ "Glossary of Meteorology - scale height". American Meteorological Society (AMS).
- ^ "Pressure Scale Height". Wolfram Research.
- ^ "2018 CODATA Value: Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ "Daniel J. Jacob: "Introduction to Atmospheric Chemistry", Princeton University Press, 1999". Archived from the original on 2013-04-10. Retrieved 2013-04-18.
- ^ "Example: The scale height of the Earth's atmosphere" (PDF). Archived from the original (PDF) on 2011-07-16.
- ^ "Venus Fact Sheet". NASA. Retrieved 28 September 2013.
- ^ "Earth Fact Sheet". NASA. Retrieved 28 September 2013.
- ^ "Mars Fact Sheet". NASA. Retrieved 28 September 2013.
- ^ "Jupiter Fact Sheet". NASA. Archived from the original on 13 October 2011. Retrieved 28 September 2013.
- ^ "Saturn Fact Sheet". NASA. Archived from the original on 18 August 2011. Retrieved 28 September 2013.
- ^ Justus, C. G.; Aleta Duvall; Vernon W. Keller (1 August 2003). "Engineering-Level Model Atmospheres For Titan and Mars". International Workshop on Planetary Probe Atmospheric Entry and Descent Trajectory Analysis and Science, Lisbon, Portugal, October 6–9, 2003, Proceedings: ESA SP-544. ESA. Retrieved 28 September 2013.
- ^ "Uranus Fact Sheet". NASA. Retrieved 28 September 2013.
- ^ "Neptune Fact Sheet". NASA. Retrieved 28 September 2013.
- ^ "Pluto Fact Sheet". NASA. Retrieved 2020-09-28.
- ^ "2018 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ Lovelace, R.V.E.; Mehanian, C.; Mobarry, C. M.; Sulkanen, M. E. (September 1986). "Theory of Axisymmetric Magnetohydrodynamic Flows: Disks". Astrophysical Journal Supplement. 62: 1. Bibcode:1986ApJS...62....1L. doi:10.1086/191132. Retrieved 26 January 2022.
- ^ Campbell, C. G.; Heptinstall, P. M. (August 1998). "Disc structure around strongly magnetic accretors: a full disc solution with turbulent diffusivity". Monthly Notices of the Royal Astronomical Society. 299 (1): 31. Bibcode:1998MNRAS.299...31C. doi:10.1046/j.1365-8711.1998.01576.x.
- ^ a b Liffman, Kurt; Bardou, Anne (October 1999). "A magnetic scaleheight: the effect of toroidal magnetic fields on the thickness of accretion discs". Monthly Notices of the Royal Astronomical Society. 309 (2): 443. Bibcode:1999MNRAS.309..443L. doi:10.1046/j.1365-8711.1999.02852.x.