In electronics, ring modulation is a signal processing function, an implementation of frequency mixing, in which two signals are combined to yield an output signal. One signal, called the carrier, is typically a sine wave or another simple waveform; the other signal is typically more complicated and is called the input or the modulator signal. A ring modulator is an electronic device for ring modulation. A ring modulator may be used in music synthesizers and as an effects unit.
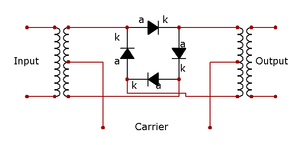

The name derives from the fact that the analog circuit of diodes originally used to implement this technique takes the shape of a ring: a diode ring.[2] The circuit is similar to a bridge rectifier, except that instead of the diodes facing left or right, they face clockwise or counterclockwise.
Ring modulation is quite similar to amplitude modulation, with the difference that in the latter the modulator is shifted to be positive before being multiplied with the carrier, while in the former the unshifted modulator is multiplied with the carrier. This has the effect that ring modulation of two sine waves having frequencies of 1,500 Hz and 400 Hz will produce as output signal the sum of a sine wave with frequency 1,900 Hz and one with frequency 1,100 Hz. These two output frequencies are known as sidebands. If one of the input signals has significant overtones (which is the case for square waves), the output will sound quite different, since each harmonic will generate its own pair of sidebands that won't be harmonically-related.[3]
Operation edit
Denoting the carrier signal by , the modulator signal by and the output signal by (where denotes time), ring modulation is described by the formula
If and are sine waves with frequencies and , respectively, then will be the sum of two (phase-shifted) sine waves, one of frequency and the other of frequency . This is a consequence of the trigonometric identity
Alternatively, one can use the fact that multiplication in the time domain is the same as convolution in the frequency domain.
Ring modulators thus output the sum and difference of the frequencies present in each waveform. This process of ring modulation produces a signal rich in partials. As well, neither the carrier nor the incoming signal are prominent in the output, and ideally, not present at all.
Two oscillators, whose frequencies were harmonically related and ring modulated against each other, produce sounds that still adhere to the harmonic partials of the notes but contain a very different spectral makeup. When the oscillators' frequencies are not harmonically related, ring modulation creates inharmonics, often producing bell-like or otherwise metallic sounds.
If the carrier signal is a square wave of frequency , whose Fourier expansion contains the fundamental and a series of reducing-amplitude odd harmonics:
and the carrier frequency is at least twice the maximum frequency of the modulating signal , then the resulting output is a series of duplicates of at increasing regions of the frequency spectrum.[4] For example, let represent a sine wave at 100 Hz, and the carrier be an ideal square wave at 300 Hz. The output will then include sine waves at 100±300 Hz, 100±900 Hz, 100±1500 Hz, 100±2100 Hz, etc., at decreasing amplitudes according to the Fourier expansion of the carrier square wave. If the carrier frequency is less than twice the upper frequency of the signal then the resulting output signal contains spectral components from both the signal and the carrier that combine in the time domain.
Because the output contains neither the individual modulator or carrier components, the ring modulator is said to be a double-balanced mixer,[5] where both input signals are suppressed (not present in the output)—the output is composed entirely of the sum of the products of the frequency components of the two inputs.
History edit
The ring modulator was invented by Frank A. Cowan in 1934 and patented in 1935[6] as an improvement on the invention of Clyde R. Keith at Bell Labs.[7] The original application was in the field of analog telephony for frequency-division multiplexing for carrying multiple voice signals over telephone cables. It has since been applied to a wider range of uses, such as voice inversion, radio transceivers, and electronic music.
While the original Cowan patent describes a circuit with a ring of four diodes, later implementations used FETs as the switching elements.
Circuit description edit
The ring modulator includes an input stage, a ring of four diodes excited by a carrier signal, and an output stage. The input and output stages typically include transformers with center-taps towards the diode ring. It is important to note that while the diode ring has some similarities to a bridge rectifier the diodes in a ring modulator all point in the same clockwise or counterclockwise direction. (See the schematic of a ring modulator in the upper right.)
The carrier, which alternates between positive and negative current, at any given time makes one pair of diodes conduct, and reverse-biases the other pair. The conducting pair carries the signal from the left transformer secondary to the primary of the transformer at the right. If the left carrier terminal is positive, the top and bottom diodes conduct. If that terminal is negative, then the side diodes conduct, but create a polarity inversion between the transformers. This action is much like that of a DPDT (double pole, double throw) switch wired for reversing connections.
A particular elegance of the ring modulator is that it is bidirectional: the signal flow can be reversed allowing the same circuit with the same carrier to be used either as a modulator or demodulator, for example in low-cost radio transceivers.
Integrated circuit methods of ring modulation edit
This section needs additional citations for verification. (February 2015) |
Some modern ring modulators are implemented using digital signal processing techniques by simply multiplying the time domain signals, producing a nearly-perfect signal output. Intermodulation products can be generated by carefully selecting and changing the frequency of the two input waveforms. If the signals are processed digitally, the frequency-domain convolution becomes circular convolution. If the signals are wideband, this will cause aliasing distortion, so it is common to oversample the operation or low-pass filter the signals prior to ring modulation.
The SID chip found in the Commodore 64 allows for triangle waves to be ring modulated. Oscillator 1 gets modulated by oscillator 3's frequency, oscillator 2 by oscillator 1's frequency, and oscillator 3 by oscillator 2's frequency. Ring modulation is disabled unless the carrier oscillator is set to produce a triangle wave, but the modulating oscillator can be set to generate any of its available waveforms. However, no matter what waveform you set the modulating oscillator to, the ring modulation will always have the effect of modulating a triangle wave with a square wave.[8][failed verification]
On an ARP Odyssey synthesizer (and a few others from that era as well) the ring modulator is an XOR function (formed from four NAND gates) fed from the square wave outputs of the two oscillators. For the limited case of square or pulse wave signals, this is identical to true ring modulation.
Analog multiplier ICs (such as those made by Analog Devices) would work as ring modulators, of course with regard to such matters as their operating limits and scale factors. Use of multiplier ICs means that the modulation products are largely confined to sum and difference frequency of inputs (unless the circuit is overdriven), rather than the much more complicated products of the rectifier circuit.
Limitations edit
Any DC component of the carrier will degrade the suppression of the carrier and thus in radio applications the carrier is typically transformer- or capacitor-coupled; in low frequency (e.g., audio) applications the carrier may or may not be desired in the output.[9]
Imperfections in the diodes and transformers introduce artifacts of the two input signals. In practical ring modulators, this leakage can be reduced by introducing opposing imbalances (e.g., variable resistors or capacitors).
Applications edit
Radio communications edit
Ring modulation has also been extensively used in radio receivers, for example, to demodulate an FM stereo signal, and to heterodyne microwave signals in mobile telephone and wireless networking systems. In this case, the circuit is sometimes called a ring demodulator, one of many possible chopper circuits.[10][11] A ring modulator can be used to generate a double-sideband suppressed-carrier (DSB-SC) wave used in radio transmission.[12]
Music and sound effects edit
One of the earliest musical instruments utilizing a ring modulator was the Melochord (1947) built by Harald Bode. It was a two-tone melody keyboard instrument with foot controllers and later added a second keyboard for timbre control, featuring a white-noise generator, envelope controller, formant filters and ring modulators for harmonics.[13] The early Melochord was extensively used by Werner Meyer-Eppler in the early days of the electronic music studio at Bonn University.[14] Meyer-Eppler mentioned the musical application of ring modulator in his book Elektrische Klangerzeugung, published in 1949.[15]
Meyer-Eppler's student Karlheinz Stockhausen used ring modulation in 1956 for some sounds in Gesang der Jünglinge and his realization score for Telemusik (1966[16]) also calls for it. Indeed, several entire compositions by Stockhausen are based around it, such as Mixtur (1964), one of the first compositions for orchestra and live electronics; Mikrophonie II (1965), where the sounds of choral voices are modulated with a Hammond organ; Mantra (1970),[16] where the sounds from two pianos are routed through ring modulators; and Licht-Bilder (2002) from Sonntag aus Licht (2003),[1] which ring-modulates flute and trumpet.[17][18][19] Other Stockhausen pieces employing ring modulation include Kontakte (1960),[1] Mikrophonie I (1964),[1] Hymnen (1969),[1] Prozession (1967),[1] and Kurzwellen (1968).[1]
A ring-modulator was the major component used in Louis and Bebe Barron's music for the film Forbidden Planet (1956). One of the best-known applications of the ring modulator may be its use by Brian Hodgson of the BBC Radiophonic Workshop to produce the distinctive voice of the Daleks in the television series Doctor Who, starting in 1963.[20]
One of the first products dedicated for music was the Bode Ring Modulator developed in 1961 by Harald Bode. Also in 1964 he developed the Bode Frequency Shifter, which produced a clearer sound by eliminating a side band.[21] These devices were designed to be controlled by voltage, compatible with modular synthesizer architecture also advocated by him,[22] and these modules were licensed to R.A. Moog for their Moog modular synthesizers started in 1963–1964.[23] In 1963, Don Buchla included an optional ring modulator in his first modular synthesizer, the Model 100.[24] Also Tom Oberheim built a ring modulator unit for his musician friend in the late 1960s,[25][26] and it became an origin of Oberheim Electronics Music Modulator[27] and Maestro Ring Modulator,[28] one of the earliest ring modulator effect products for guitarists. The EMS VCS3, Synthi A, ARP 2600, Odyssey, Rhodes Chroma and Yamaha CS-80 synthesizers also featured built-in ring modulators.
John McLaughlin employs the ring modulator heavily in the 1974 Mahavishnu Orchestra album Visions of the Emerald Beyond, especially on the track "On the Way Home to Earth". On Miles Davis' 1975 live album Agharta, guitarist Pete Cosey ran the sounds he played through a ring modulator.[29] Deep Purple's Jon Lord fed the signal from his Hammond through a Gibson Ring Modulator unit live on stage, which he described in 1989.[30][31] Founding member of Hawkwind, Dik Mik, a self-confessed non-musician, used a ring modulator as his main instrument during his time with the band (1969-1973).[32]
Vangelis used a ring modulator with his Yamaha CS-80 to improvise his 1978 avant-garde-experimental album Beaubourg. The music on the album is often atonal, with the ring modulator converting the synthesizer's sound into complex metallic timbres.[33] It remains the most experimental released work by the artist, with reviewers calling it "difficult listening at best".[34]
Ring modulation is used in the piece Ofanim (1988/1997) by Luciano Berio, and in the first section is applied to a child's voice and a clarinet: "The transformation of the child voice into a clarinet was desired. For this purpose, a pitch detector computes the instantaneous frequency of the voice. Then the child voice passes through a ring modulator, where the frequency of the carrier is set to . In this case odd harmonics prevail which is similar to the sound of a clarinet in the low register."[35][failed verification]
Analogue telephone systems edit
An early application of the ring modulator was for combining multiple analog telephone voice channels into a single wideband signal to be carried on a single cable using frequency-division multiplexing. A ring modulator in combination with carrier wave and filter was used to assign channels to different frequencies.
Early attempts at securing analog telephone channels used ring modulators to modify the spectrum of the audio speech signals. One application is spectral inversion, typically of speech; a carrier frequency is chosen to be above the highest speech frequencies (which are low-pass filtered at, say, 3 kHz, for a carrier of perhaps 3.3 kHz), and the sum frequencies from the modulator are removed by more low-pass filtering. The remaining difference frequencies have an inverted spectrum: high frequencies become low, and vice versa.
See also edit
References edit
- ^ a b c d e f g h Curtis Roads (1996). The Computer Music Tutorial, pp. 220-221. MIT Press. ISBN 9780262680820.
- ^ Richard Orton, "Ring Modulator", The New Grove Dictionary of Music and Musicians, page 429, volume 21, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan Publishers, 2001): "the ring modulator takes its name from the characteristic ring formation of four diodes in its analog circuit."
- ^ Strange, Allen (1972). Electronic Music, p. 11. Wm. C. Brown Co. Publishers. ISBN 0-697-03612-X.
- ^ "Multipliers vs. Modulators".
- ^ "Double Balanced Mixer – Theory; Circuit; Operation – Tutorial – Electronics Notes".
- ^ U.S. patent 2,025,158
- ^ U.S. patent 1,855,576
- ^ Commodore Programmer's Reference Guide, page 463
- ^ "Synth Secrets, Part 11: Amplitude Modulation".
- ^ Hamish Meikle (2008). Modern Radar Systems. Artech House. p. 336. ISBN 978-1-59693-243-2.
- ^ Abhishek Yadav (2008). Analog Communication System. Firewall Media. p. 83. ISBN 978-81-318-0319-6.
- ^ T G Thomas S Chandra Sekhar (2005). Communication Theory. Tata McGraw-Hill Education. p. 37. ISBN 978-0-07-059091-5.
- ^ Rebekkah Palov (July 2011), "Harald Bode—A Short Biography", EContact!, 13 (4), Canadian Electroacoustic Community
- ^ "The "Melochord" (1947–9)", The Keyboardmuseum Online, archived from the original on 14 November 2007 (description and history)
- ^ Werner Meyer-Eppler, Elektronische Klangerzeugung: Elektronische Musik und synthetische Sprache, (Bonn: Ferdinand Dümmlers, 1949)
- ^ a b Collins, Nick (2010). Introduction to Computer Music, pp. 124-125. John Wiley & Sons. ISBN 9780470714553.
- ^ Ludger Brümmer, "Stockhausen on Electronics, 2004", Computer Music Journal 32, no. 4 (2008):10–16.
- ^ Karlheinz Stockhausen, "Electroacoustic Performance Practice", translated by Jerome Kohl, Perspectives of New Music 34, no. 1 (Winter, 1996): 74–105. Citation on 89.
- ^ Karlheinz Stockhausen, "Einführung"/"Introduction", English translation by Suzanne Stephens, in booklet accompanying Karlheinz Stockhausen, Licht-Bilder (3. Szene vom SONNTAG aus LICHT), 2-CD set, Stockhausen Gesamtausgabe/Complete Edition 68A–B (Kürten: Stockhausen-Verlag, 2005): 10 & 51
- ^ Jeremy Bentham (1986), Doctor Who: The Early Years, (London: W. H. Allen & Co., 1986), p. 127, ISBN 0-491-03612-4
- ^ Harald Bode—A Lifetime for Sound (PDF), Harald Bode News, retrieved 27 January 2011
- ^ Harald Bode, "European Electronic Music Instrument Design", Journal of the Audio Engineering Society 9 (1961): 267.
- ^ Tom Rhea (21 March 2011), Harald Bode Biography, (New York: Experimental Television Center Ltd, 2004), archived from the original on 19 July 2011
- ^ Buchla Electronic Musical Instruments—Historical Overview, Buchla & Associates, retrieved 27 January 2011
- ^ Thomas E. Oberheim, "A Ring Modulator Device for the Performing Musician", AES Convention 38 (May 1970), No. 708 (G-4).
- ^ "Session Transcript: Tom Oberheim", Red Bull Music Academy Barcelona 2008
- ^ Oberheim Music Modulator (photo). Edison Music Corporation.
- ^ Maestro RM-1A Ring Modulator, DiscoFreq's Effects Database
- ^ Trzaskowski, Andrzej (1976). Jazz Forum: The Magazine of the International Jazz Federation: 74.
Most of the selections are kept in the rock-jazz climate with the rhythm course being interrupted now and again by an overflowing patch of accumulated layers of electronic and percussive effects (Theme from Jack Johnson, Prelude). In fact, electronic effects appear repeatedly in the form of 'bruitistic' whizzes and grinds of the synthi resembling a buzz saw and of the guitar steered through a ring modulator.
{{cite journal}}: Missing or empty|title=(help) - ^ "Lord Almighty". Keyboard. 24. 1998. Retrieved 21 January 2016.
- ^ "Interview with Jon Lord". Modern Keyboard. January 1989. Retrieved 21 January 2015.
- ^ Ian Abrahams (2004). Hawkwind: Sonic Assassins. SAF Publishing. p. 20. ISBN 9780946719693.
- ^ "Vangelis - Beaubourg". Synthtopia. 7 December 2003. Retrieved 26 August 2022.
- ^ McDonald, Steven. "Vangelis - Beaubourg". AllMusic. Retrieved 26 August 2022.
- ^ Zölzer, Udo; ed. (2002). DAFX - Digital Audio Effects, p.76-7. John Wiley & Sons. ISBN 9780471490784.
External links edit
- Scott Lehman. "Effects Explained: Ring Modulation". Harmony Central. Archived from the original on 1 December 2005.

