In geometry, a pentakis dodecahedron or kisdodecahedron is a polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. Specifically, the term typically refers to a particular Catalan solid, namely the dual of a truncated icosahedron.
| Pentakis dodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kD |
| Face type | V5.6.6 isosceles triangle |
| Faces | 60 |
| Edges | 90 |
| Vertices | 32 |
| Vertices by type | 20{6}+12{5} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 156°43′07″ arccos(−80 + 9√5/109) |
| Properties | convex, face-transitive |
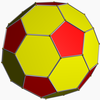 Truncated icosahedron (dual polyhedron) |
 Net |

Cartesian coordinates edit
Let be the golden ratio. The 12 points given by and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points together with the points and cyclic permutations of these coordinates. Multiplying all coordinates of the icosahedron by a factor of gives a slightly smaller icosahedron. The 12 vertices of this icosahedron, together with the vertices of the dodecahedron, are the vertices of a pentakis dodecahedron centered at the origin. The length of its long edges equals . Its faces are acute isosceles triangles with one angle of and two of . The length ratio between the long and short edges of these triangles equals .
Chemistry edit
The pentakis dodecahedron in a model of buckminsterfullerene: each (spherical) surface segment represents a carbon atom, and if all are replaced with planar faces, a pentakis dodecahedron is produced. Equivalently, a truncated icosahedron is a model of buckminsterfullerene, with each vertex representing a carbon atom.
Biology edit
The pentakis dodecahedron is also a model of some icosahedrally symmetric viruses, such as Adeno-associated virus. These have 60 symmetry related capsid proteins, which combine to make the 60 symmetrical faces of a pentakis dodecahedron.
Orthogonal projections edit
The pentakis dodecahedron has three symmetry positions, two on vertices, and one on a midedge:
| Projective symmetry |
[2] | [6] | [10] |
|---|---|---|---|
| Image | |||
| Dual image |
Concave pentakis dodecahedron edit
A concave pentakis dodecahedron replaces the pentagonal faces of a dodecahedron with inverted pyramids.
Related polyhedra editThe faces of a regular dodecahedron may be replaced (or augmented with) any regular pentagonal pyramid to produce what is in general referred to as an elevated dodecahedron. For example, if pentagonal pyramids with equilateral triangles are used, the result is a non-convex deltahedron. Any such elevated dodecahedron has the same combinatorial structure as a pentakis dodecahedron, i.e., the same Schlegel diagram.
See also editCultural references edit
References edit
External links edit
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||