This article includes a list of general references, but it lacks sufficient corresponding inline citations. (December 2011) |
In probability and statistics, the Gompertz distribution is a continuous probability distribution, named after Benjamin Gompertz. The Gompertz distribution is often applied to describe the distribution of adult lifespans by demographers[1][2] and actuaries.[3][4] Related fields of science such as biology[5] and gerontology[6] also considered the Gompertz distribution for the analysis of survival. More recently, computer scientists have also started to model the failure rates of computer code by the Gompertz distribution.[7] In Marketing Science, it has been used as an individual-level simulation for customer lifetime value modeling.[8] In network theory, particularly the Erdős–Rényi model, the walk length of a random self-avoiding walk (SAW) is distributed according to the Gompertz distribution.[9]
|
Probability density function 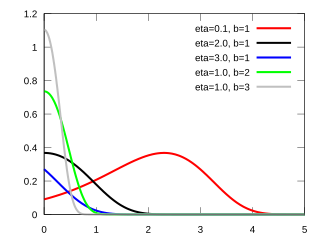 | |||
|
Cumulative distribution function  | |||
| Parameters | shape , scale | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean |
| ||
| Median | |||
| Mode |
| ||
| Variance |
| ||
| MGF |
| ||
Specification edit
Probability density function edit
The probability density function of the Gompertz distribution is:
where is the scale parameter and is the shape parameter of the Gompertz distribution. In the actuarial and biological sciences and in demography, the Gompertz distribution is parametrized slightly differently (Gompertz–Makeham law of mortality).
Cumulative distribution function edit
The cumulative distribution function of the Gompertz distribution is:
where and
Moment generating function edit
The moment generating function is:
where
Properties edit
The Gompertz distribution is a flexible distribution that can be skewed to the right and to the left. Its hazard function is a convex function of . The model can be fitted into the innovation-imitation paradigm with as the coefficient of innovation and as the coefficient of imitation. When becomes large, approaches . The model can also belong to the propensity-to-adopt paradigm with as the propensity to adopt and as the overall appeal of the new offering.
Shapes edit
The Gompertz density function can take on different shapes depending on the values of the shape parameter :
- When the probability density function has its mode at 0.
- When the probability density function has its mode at
Kullback-Leibler divergence edit
If and are the probability density functions of two Gompertz distributions, then their Kullback-Leibler divergence is given by
where denotes the exponential integral and is the upper incomplete gamma function.[10]
Related distributions edit
- If X is defined to be the result of sampling from a Gumbel distribution until a negative value Y is produced, and setting X=−Y, then X has a Gompertz distribution.
- The gamma distribution is a natural conjugate prior to a Gompertz likelihood with known scale parameter [8]
- When varies according to a gamma distribution with shape parameter and scale parameter (mean = ), the distribution of is Gamma/Gompertz.[8]
- If , then , and hence .[12]
Applications edit
- In hydrology the Gompertz distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Gompertz distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
See also edit
Notes edit
- ^ Vaupel, James W. (1986). "How change in age-specific mortality affects life expectancy" (PDF). Population Studies. 40 (1): 147–157. doi:10.1080/0032472031000141896. PMID 11611920.
- ^ Preston, Samuel H.; Heuveline, Patrick; Guillot, Michel (2001). Demography:measuring and modeling population processes. Oxford: Blackwell.
- ^ Benjamin, Bernard; Haycocks, H.W.; Pollard, J. (1980). The Analysis of Mortality and Other Actuarial Statistics. London: Heinemann.
- ^ Willemse, W. J.; Koppelaar, H. (2000). "Knowledge elicitation of Gompertz' law of mortality". Scandinavian Actuarial Journal. 2000 (2): 168–179. doi:10.1080/034612300750066845. S2CID 122719776.
- ^ Economos, A. (1982). "Rate of aging, rate of dying and the mechanism of mortality". Archives of Gerontology and Geriatrics. 1 (1): 46–51. doi:10.1016/0167-4943(82)90003-6. PMID 6821142.
- ^ Brown, K.; Forbes, W. (1974). "A mathematical model of aging processes". Journal of Gerontology. 29 (1): 46–51. doi:10.1093/geronj/29.1.46. PMID 4809664.
- ^ Ohishi, K.; Okamura, H.; Dohi, T. (2009). "Gompertz software reliability model: estimation algorithm and empirical validation". Journal of Systems and Software. 82 (3): 535–543. doi:10.1016/j.jss.2008.11.840.
- ^ a b c Bemmaor, Albert C.; Glady, Nicolas (2012). "Modeling Purchasing Behavior With Sudden 'Death': A Flexible Customer Lifetime Model". Management Science. 58 (5): 1012–1021. doi:10.1287/mnsc.1110.1461.
- ^ Tishby, Biham, Katzav (2016), The distribution of path lengths of self avoiding walks on Erdős-Rényi networks, arXiv:1603.06613.
- ^ Bauckhage, C. (2014), Characterizations and Kullback-Leibler Divergence of Gompertz Distributions, arXiv:1402.3193.
- ^ Calculator for probability distribution fitting [1]
- ^ Kleiber, Christian; Kotz, Samuel (2003). Statistical Size Distributions in Economics and Actuarial Sciences. Wiley. p. 179. doi:10.1002/0471457175. ISBN 9780471150640.
References edit
- Bemmaor, Albert C.; Glady, Nicolas (2011). "Implementing the Gamma/Gompertz/NBD Model in MATLAB" (PDF). Cergy-Pontoise: ESSEC Business School.[permanent dead link]
- Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society of London. 115: 513–583. doi:10.1098/rstl.1825.0026. JSTOR 107756. S2CID 145157003.
- Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd ed.). New York: John Wiley & Sons. pp. 25–26. ISBN 0-471-58494-0.
- Sheikh, A. K.; Boah, J. K.; Younas, M. (1989). "Truncated Extreme Value Model for Pipeline Reliability". Reliability Engineering and System Safety. 25 (1): 1–14. doi:10.1016/0951-8320(89)90020-3.








![{\displaystyle \left(1/b\right)\ln \left[\left(1/\eta \right)\ln \left(1/2\right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2025ab32684a86966829b308bb1452815fe57bf)




![{\displaystyle +\left(\pi ^{2}/6\right)+2\gamma \ln \left(\eta \right)+[\ln \left(\eta \right)]^{2}-e^{\eta }[{\text{Ei}}\left(-\eta \right)]^{2}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0850883c7b5814914301c155e014ceb896b962b7)

![{\displaystyle {\begin{aligned}{\text{ and }}{}_{3}{\text{F}}_{3}&\left(1,1,1;2,2,2;-z\right)=\\&\sum _{k=0}^{\infty }\left[1/\left(k+1\right)^{3}\right]\left(-1\right)^{k}\left(z^{k}/k!\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/119de9d74e9e1513410d20f25e74f7b7336a0948)

