Half maximal effective concentration (EC50) is a measure of the concentration of a drug, antibody or toxicant which induces a biological response halfway between the baseline and maximum after a specified exposure time.[1] More simply, EC50 can be defined as the concentration required to obtain a 50% [...] effect[2] and may be also written as [A]50.[3] It is commonly used as a measure of a drug's potency, although the use of EC50 is preferred over that of 'potency', which has been criticised for its vagueness.[3] EC50 is a measure of concentration, expressed in molar units (M), where 1 M is equivalent to 1 mol/L.
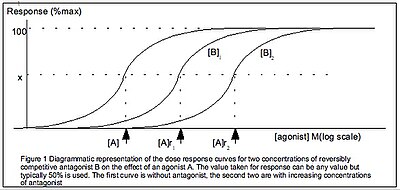
The EC50 of a graded dose response curve therefore represents the concentration of a compound where 50% of its maximal effect is observed.[4] The EC50 of a quantal dose response curve represents the concentration of a compound where 50% of the population exhibit a response,[5] after a specified exposure duration.
For clarification, a graded dose response curve shows the graded effect of the drug (y axis) over the dose of the drug (x axis) in one or an average of subjects. A quantal dose response curve shows the percentage of subjects where a response is noted in an all-or-none manner (y axis) over the dose of the drug (x axis).
For competition binding assays and functional antagonist assays IC50 is the most common summary measure of the dose-response curve. For agonist/stimulator assays the most common summary measure is the EC50.[6]
The EC50 is also related to IC50 which is a measure of a compound's inhibition (50% inhibition).
Calculation of EC50 edit
Biological responses to ligand concentrations typically follow a sigmoidal function. The inflection point at which the increase in response with increasing ligand concentration begins to slow is the EC50, which can be mathematically determined by derivation of the best-fit line. While relying on a graph for estimation is more convenient, this typical method yields less accurate results and less precise.[6]
The response or effect, E, is dependent on both the binding of the drug and the drug-bound receptor. The agonist that binds to the receptor and initiates the response is usually abbreviated A or D. At low agonist concentrations, [A], the response, E is immeasurably low but at higher [A], E becomes measurable. E increases with [A] until at sufficiently high [A], when E plateaus towards an asymptotic maximum attainable response, Emax. The [A] at which E is 50% of Emax is termed the half maximal effective concentration and is abbreviated EC50, or rarely [A]50. The term "potency" refers to the EC50 value. The lower the EC50, the less the concentration of a drug is required to produce 50% of maximum effect and the higher the potency. The EC10 and EC90 concentrations to induce 10% and 90% maximal responses are defined similarly.
There is a wide range of EC50 values of drugs; they are typically anywhere from nM to mM. Hence, it is often more practical to refer to the logarithmically transformed pEC50 values instead of EC50, where
.
Relation to affinity and efficacy edit
A drug's potency is dependent on the drug's affinity and efficacy.
Affinity edit
Affinity describes how well a drug can bind to a receptor. Faster or stronger binding is represented by a higher affinity, or equivalently a lower dissociation constant. The EC50 should not be confused with the affinity constant, Kd. While the former reflects the drug concentration needed for a level of tissue response, the latter reflects the drug concentration needed for an amount of receptor binding.
Efficacy edit
Efficacy is the relationship between receptor occupancy and the ability to initiate a response at the molecular, cellular, tissue or system level.
Relation to the Hill Equation edit
The EC50 relates to the Hill equation, which is a function of the agonist concentration, [A]:
where E is the observed response or effect above baseline, and n, the Hill coefficient reflects the slope of the curve.[7]
The EC50 represents the point of inflection of the Hill equation, beyond which increases of [A] have less impact on E. In dose response curves, the logarithm of [A] is often taken, turning the Hill equation into a sigmoidal logistic function. In this case, the EC50 represents the rising section of the sigmoid curve.
Limitations edit
The effects of a stressor or drug generally depend on the exposure time. Therefore, the EC50 (and similar statistics) will be a function of exposure time. The exact shape of this time function will depend upon the stressor (e.g., the specific toxicant), its mechanism of action, the organism exposed, etc. This time dependency hampers the comparison of potency or toxicity between compounds and between different organisms.
A drug will not have a single value of EC50 due to different tissues having different sensitivities to the drug (in part due to tissue specific receptor expression).[citation needed] Furthermore, EC50 is dependent on many factors including species, tissue and cell type and genetics.[citation needed]
See also edit
- Measures of pollutant concentration
- Certain safety factor
- LD50 (median lethal dose)
- Therapeutic index
References edit
- ^ "Introducing dose response curves". Graphpad Software. Archived from the original on 2012-07-30.
- ^ Chen, Zheng; Bertin, Riccardo; Froldi, Guglielmina (2013-05-01). "EC50 estimation of antioxidant activity in DPPH assay using several statistical programs". Food Chemistry. 138 (1): 414–420. doi:10.1016/j.foodchem.2012.11.001. ISSN 0308-8146. PMID 23265506.
- ^ a b c Neubig, Richard R. (2003). "International Union of Pharmacology Committee on Receptor Nomenclature and Drug Classification. XXXVIII. Update on Terms and Symbols in Quantitative Pharmacology" (PDF). Pharmacological Reviews. 55 (4): 597–606. doi:10.1124/pr.55.4.4. PMID 14657418. S2CID 1729572.
- ^ "Northwestern Molbiosci EC50 definition". Archived from the original on 2010-06-14. Retrieved 2019-05-27.
- ^ "Drug Dose and Clinical Response". Archived from the original on 2007-02-20. Retrieved 2019-04-16.
- ^ a b Assay Operations for SAR Support Archived 2006-11-29 at the Wayback Machine NIH Chemical Genomics Center
- ^ EC50 equation Archived 2012-04-17 at the Wayback Machine