In the context of digital signal processing (DSP), a digital signal is a discrete time, quantized amplitude signal. In other words, it is a sampled signal consisting of samples that take on values from a discrete set (a countable set that can be mapped one-to-one to a subset of integers). If that discrete set is finite, the discrete values can be represented with digital words of a finite width. Most commonly, these discrete values are represented as fixed-point words (either proportional to the waveform values or companded) or floating-point words.[1][2][3][4][5]

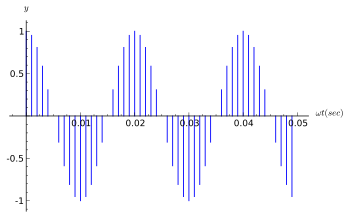
The process of analog-to-digital conversion produces a digital signal.[6] The conversion process can be thought of as occurring in two steps:
- sampling, which produces a continuous-valued discrete-time signal, and
- quantization, which replaces each sample value with an approximation selected from a given discrete set (for example, by truncating or rounding).
It can be shown that an analog signal can be reconstructed after conversion to digital (down to the precision afforded by the quantization used), provided that the signal has negligible power in frequencies above the Nyquist limit and does not saturate the quantizer.
Common practical digital signals are represented as 8-bit (256 levels), 16-bit (65,536 levels), 24-bit (16.8 million levels), and 32-bit (4.3 billion levels) using pulse-code modulation where the number of quantization levels is not necessarily limited to powers of two. A floating point representation is used in many DSP applications.
References edit
- ^ Smith, Steven W. (2002-11-06). "3". Digital Signal Processing: A Practical Guide for Engineers and Scientists. Demystifying Technology. Vol. 1 (1 ed.). Newnes. pp. 35–39. ISBN 075067444X.
- ^ Harris, Frederic J. (2004-05-24). "1.1". Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR. p. 2. ISBN 0131465112.
- ^ Vaseghi, Saeed V. (2009-03-02). "1.4". Advanced Digital Signal Processing and Noise Reduction (4 ed.). Chichester, West Suffix, United Kingdom: John Wiley & Sons. p. 23. ISBN 0470754060.
- ^ Diniz, Paulo S. R.; Eduardo A. B. da Silva; Sergio L. Netto (2010-09-13). "1.1". Digital Signal Processing: System Analysis and Design (2 ed.). New York & UK: Cambridge University Press. p. 5. ISBN 0521887755.
- ^ Manolakis, Dimitris G.; Vinay K. Ingle (2011-11-21). "1.1.1". Applied Digital Signal Processing: Theory and Practice. Cambridge, UK: Cambridge University Press. p. 5. ISBN 0521110025.
- ^ Ingle, Vinay K.; John G. Proakis (2011-01-01). "1.1". Digital Signal Processing Using MATLAB (3 ed.). Stamford, CT: CL Engineering. p. 3. ISBN 1111427372.