In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). ⓘ Each step represents a frequency ratio of 21⁄53, or 22.6415 cents (ⓘ), an interval sometimes called the Holdrian comma.
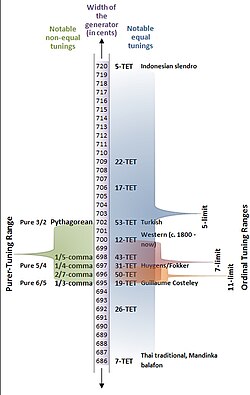
53-TET is a tuning of equal temperament in which the tempered perfect fifth is 701.89 cents wide, as shown in Figure 1.
The 53-TET tuning equates to the unison, or tempers out, the intervals 32805⁄32768, known as the schisma, and 15625⁄15552, known as the kleisma. These are both 5 limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53 ET tempers out both characterizes it completely as a 5 limit temperament: it is the only regular temperament tempering out both of these intervals, or commas, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka. Because it tempers these out, 53-TET can be used for both schismatic temperament, tempering out the schisma, and Hanson temperament (also called kleismic), tempering out the kleisma.
The interval of 7⁄4 is 4.8 cents sharp in 53-TET, and using it for 7-limit harmony means that the septimal kleisma, the interval 225⁄224, is also tempered out.
History and use edit
Theoretical interest in this division goes back to antiquity. Jing Fang (78–37 BCE), a Chinese music theorist, observed that a series of 53 just fifths ([3⁄2]53) is very nearly equal to 31 octaves (231). He calculated this difference with six-digit accuracy to be 177147⁄176776.[2][3] Later the same observation was made by the mathematician and music theorist Nicholas Mercator (c. 1620–1687), who calculated this value precisely as (353)⁄(284) = 19383245667680019896796723⁄19342813113834066795298816,[verification needed] which is known as Mercator's comma.[4] Mercator's comma is of such small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1⁄53 of that comma (≈ 0.0682 cent ≈ 1⁄315 syntonic comma ≈ 1⁄344 pythagorean comma). Thus, 53 tone equal temperament is for all practical purposes equivalent to an extended Pythagorean tuning.
After Mercator, William Holder published a treatise in 1694 which pointed out that 53 equal temperament also very closely approximates the just major third (to within 1.4 cents), and consequently 53 equal temperament accommodates the intervals of 5 limit just intonation very well.[5][6] This property of 53-TET may have been known earlier; Isaac Newton's unpublished manuscripts suggest that he had been aware of it as early as 1664–1665.[7]
Music edit
In the 19th century, people began devising instruments in 53 TET, with an eye to their use in playing near-just 5-limit music. Such instruments were devised by R.H.M. Bosanquet[8](p 328–329) and the American tuner J.P. White.[8](p 329) Subsequently, the temperament has seen occasional use by composers in the west, and by the early 20th century, 53 TET had become the most common form of tuning in Ottoman classical music, replacing its older, unequal tuning. Arabic music, which for the most part bases its theory on quartertones, has also made some use of it; the Syrian violinist and music theorist Twfiq Al-Sabagh proposed that instead of an equal division of the octave into 24 parts a 24 note scale in 53 TET should be used as the master scale for Arabic music.[citation needed]
Croatian composer Josip Štolcer-Slavenski wrote one piece, which has never been published, which uses Bosanquet's Enharmonium during its first movement, entitled Music for Natur-ton-system.[9][10][11] Furthermore, General Thompson worked in league with the London-based guitar maker Louis Panormo to produce the Enharmonic Guitar.[12]
Notation edit
Attempting to use standard notation, seven letter notes plus sharps or flats, can quickly become confusing. This is unlike the case with 19 TET and 31 TET where there is little ambiguity. By not being meantone, it adds some problems that require more attention. Specifically, the major third is different from a ditone, two tones, each of which is two fifths minus an octave. Likewise, the minor third is different from a semiditone. The fact that the syntonic comma is not tempered out means that notes and intervals need to be defined more precisely. Ottoman classical music uses a notation of flats and sharps for the 9 comma tone.
In this article, diatonic notation will be used creating the following chromatic scale, where sharps and flats aren't enharmonic, with the exception of only two pairs of pitches:
For all the other notes, the various triple and quadruple sharps and flats are different pitches.
C, C♯, C , C♯ , C , D , D , D , D♭,
D, D♯, D , D♯ , D , E , E , E , E♭,
F, F♯, F , F♯ , F , G , G , G , G♭,
G, G♯, G , G♯ , G , A , A , A , A♭,
A, A♯, A , A♯ , A , B , B , B , B♭,
Another possible notation, based on Pythagorean fifths:
C, B♯, A♯ , E , D♭, C♯, B , F , E ,
D, C , B♯ , F , E♭, D♯, C♯ , G , F♭,
F, E♯, D♯ , A , G♭, F♯, E , D /B , A ,
G, F , E♯ , B , A♭, G♯, F♯ , C , B ,
A, G , F /D , C , B♭, A♯, G♯ , D , C♭,
Chords of 53 equal temperament edit
Since 53-TET is a Pythagorean system, with nearly pure fifths, major and minor triads cannot be spelled in the same manner as in a meantone tuning. Instead, the major triads are chords like C-F♭-G (using the Pythagorean-based notation), where the major third is a diminished fourth; this is the defining characteristic of schismatic temperament. Likewise, the minor triads are chords like C-D♯-G. In 53-TET, the dominant seventh chord would be spelled C-F♭-G-B♭, but the otonal tetrad is C-F♭-G-C , and C-F♭-G-A♯ is still another seventh chord. The utonal tetrad, the inversion of the otonal tetrad, is spelled C-D♯-G-G .
Further septimal chords are the diminished triad, having the two forms C-D♯-G♭ and C-F -G♭, the subminor triad, C-F -G, the supermajor triad C-D -G, and corresponding tetrads C-F -G-B and C-D -G-A♯. Since 53-TET tempers out the septimal kleisma, the septimal kleisma augmented triad C-F♭-B in its various inversions is also a chord of the system. So is the Orwell tetrad, C-F♭-D -G in its various inversions.
Because 53-TET is compatible with both the schismatic temperament and the syntonic temperament, it can be used as a pivot tuning in a temperament modulation (a musical effect enabled by dynamic tonality).
Interval size edit
Because a distance of 31 steps in this scale is almost precisely equal to a just perfect fifth, in theory this scale can be considered a slightly tempered form of Pythagorean tuning that has been extended to 53 tones. As such the intervals available can have the same properties as any Pythagorean tuning, such as fifths that are (practically) pure, major thirds that are wide from just (about 81⁄64 opposed to the purer 5⁄4, and minor thirds that are conversely narrow (32⁄27 compared to 6⁄5).
However, 53-TET contains additional intervals that are very close to just intonation. For instance, the interval of 17 steps is also a major third, but only 1.4 cents narrower than the very pure just interval 5⁄4. 53-TET is very good as an approximation to any interval in 5 limit just intonation. Similarly, the pure just interval 6⁄5 is only 1.3 cents wider than 14 steps in 53-TET.
The matches to the just intervals involving the 7th harmonic are slightly less close (43 steps are 4.8 cents sharp for 7⁄4), but all such intervals are still quite closely matched with the highest deviation being the 7⁄5 tritone. The 11th harmonic and intervals involving it are less closely matched, as illustrated by the undecimal neutral seconds and thirds in the table below. 7-limit ratios are colored light gray, and 11- and 13-limit ratios are colored dark gray.
| Size (steps) |
Size (cents) |
Interval name | Just ratio |
Just (cents) |
Error (cents) |
Limit |
|---|---|---|---|---|---|---|
| 53 | 1200.00 | perfect octave | 2:1 | 1200.00 | 0 | 2 |
| 48 | 1086.79 | classic major seventh | 15:8 | 1088.27 | −1.48 | 5 |
| 45 | 1018.87 | just minor seventh | 9:5 | 1017.60 | +1.27 | 5 |
| 44 | 996.23 | Pythagorean minor seventh | 16:9 | 996.09 | +0.14 | 3 |
| 43 | 973.59 | harmonic seventh | 7:4 | 968.83 | +4.76 | 7 |
| 39 | 883.02 | major sixth | 5:3 | 884.36 | −1.34 | 5 |
| 37 | 837.73 | tridecimal neutral sixth | 13:8 | 840.53 | −2.8 | 13 |
| 36 | 815.09 | minor sixth | 8:5 | 813.69 | +1.40 | 5 |
| 31 | 701.89 | perfect fifth | 3:2 | 701.96 | −0.07 | 3 |
| 30 | 679.25 | grave fifth | 40:27 | 680.45 | −1.21 | 5 |
| 27 | 611.32 | Pythagorean augmented fourth | 729:512 | 611.73 | −0.41 | 3 |
| 26 | 588.68 | diatonic tritone | 45:32 | 590.22 | −1.54 | 5 |
| 26 | 588.68 | septimal tritone | 7:5 | 582.51 | +6.17 | 7 |
| 25 | 566.04 | classic tritone | 25:18 | 568.72 | −2.68 | 5 |
| 24 | 543.40 | undecimal major fourth | 11:8 | 551.32 | −7.92 | 11 |
| 24 | 543.40 | double diminished fifth | 512:375 | 539.10 | +4.30 | 5 |
| 24 | 543.40 | undecimal augmented fourth | 15:11 | 536.95 | +6.45 | 11 |
| 23 | 520.76 | acute fourth | 27:20 | 519.55 | +1.21 | 5 |
| 22 | 498.11 | perfect fourth | 4:3 | 498.04 | +0.07 | 3 |
| 21 | 475.47 | grave fourth | 320:243 | 476.54 | −1.07 | 5 |
| 21 | 475.47 | septimal narrow fourth | 21:16 | 470.78 | +4.69 | 7 |
| 20 | 452.83 | classic augmented third | 125:96 | 456.99 | −4.16 | 5 |
| 20 | 452.83 | tridecimal augmented third | 13:10 | 454.21 | −1.38 | 13 |
| 19 | 430.19 | septimal major third | 9:7 | 435.08 | −4.90 | 7 |
| 19 | 430.19 | classic diminished fourth | 32:25 | 427.37 | +2.82 | 5 |
| 18 | 407.54 | Pythagorean ditone | 81:64 | 407.82 | −0.28 | 3 |
| 17 | 384.91 | just major third | 5:4 | 386.31 | −1.40 | 5 |
| 16 | 362.26 | grave major third | 100:81 | 364.80 | −2.54 | 5 |
| 16 | 362.26 | neutral third, tridecimal | 16:13 | 359.47 | +2.79 | 13 |
| 15 | 339.62 | neutral third, undecimal | 11:9 | 347.41 | −7.79 | 11 |
| 15 | 339.62 | acute minor third | 243:200 | 337.15 | +2.47 | 5 |
| 14 | 316.98 | just minor third | 6:5 | 315.64 | +1.34 | 5 |
| 13 | 294.34 | Pythagorean semiditone | 32:27 | 294.13 | +0.21 | 3 |
| 12 | 271.70 | classic augmented second | 75:64 | 274.58 | −2.88 | 5 |
| 12 | 271.70 | septimal minor third | 7:6 | 266.87 | +4.83 | 7 |
| 11 | 249.06 | classic diminished third | 144:125 | 244.97 | +4.09 | 5 |
| 10 | 226.41 | septimal whole tone | 8:7 | 231.17 | −4.76 | 7 |
| 10 | 226.41 | diminished third | 256:225 | 223.46 | +2.95 | 5 |
| 9 | 203.77 | whole tone, major tone | 9:8 | 203.91 | −0.14 | 3 |
| 8 | 181.13 | whole tone, minor tone | 10:9 | 182.40 | −1.27 | 5 |
| 7 | 158.49 | neutral second, greater undecimal | 11:10 | 165.00 | −6.51 | 11 |
| 7 | 158.49 | grave whole tone | 800:729 | 160.90 | −2.41 | 5 |
| 7 | 158.49 | neutral second, lesser undecimal | 12:11 | 150.64 | +7.85 | 11 |
| 6 | 135.85 | major diatonic semitone | 27:25 | 133.24 | +2.61 | 5 |
| 5 | 113.21 | Pythagorean major semitone | 2187:2048 | 113.69 | −0.48 | 3 |
| 5 | 113.21 | just diatonic semitone | 16:15 | 111.73 | +1.48 | 5 |
| 4 | 90.57 | major limma | 135:128 | 92.18 | −1.61 | 5 |
| 4 | 90.57 | Pythagorean minor semitone | 256:243 | 90.22 | +0.34 | 3 |
| 3 | 67.92 | just chromatic semitone | 25:24 | 70.67 | −2.75 | 5 |
| 3 | 67.92 | greater diesis | 648:625 | 62.57 | +5.35 | 5 |
| 2 | 45.28 | just diesis | 128:125 | 41.06 | +4.22 | 5 |
| 1 | 22.64 | syntonic comma | 81:80 | 21.51 | +1.14 | 5 |
| 0 | 0.00 | perfect unison | 1:1 | 0.00 | 0.00 | 1 |
Scale diagram edit
The following are 21 of the 53 notes in the chromatic scale. The rest can easily be added.
Holdrian comma edit
In music theory and musical tuning the Holdrian comma, also called Holder's comma, and rarely the Arabian comma,[13] is a small musical interval of approximately 22.6415 cents,[13] equal to one step of 53 equal temperament, or (ⓘ). The name comma is misleading, since this interval is an irrational number and does not describe the compromise between intervals of any tuning system; it assumes this name because it is an approximation of the syntonic comma (21.51 cents)(ⓘ), which was widely used as a measurement of tuning in William Holder's time.
The origin of Holder's comma resides in the fact that the Ancient Greeks (or at least Boethius[14]) believed that in the Pythagorean tuning the tone could be divided in nine commas, four of which forming the diatonic semitone and five the chromatic semitone. If all these commas are exactly of the same size, there results an octave of 5 tones + 2 diatonic semitones, 5 × 9 + 2 × 4 = 53 equal commas. Holder[15] attributes the division of the octave in 53 equal parts to Nicholas Mercator,[16] who would have named the 1/53 part of the octave the "artificial comma".
Mercator's comma and the Holdrian comma edit
Mercator's comma is a name often used for a closely related interval because of its association with Nicholas Mercator.[17] One of these intervals was first described by Ching-Fang in 45 BCE.[13] Mercator applied logarithms to determine that (≈ 21.8182 cents) was nearly equivalent to a syntonic comma of ≈ 21.5063 cents (a feature of the prevalent meantone temperament of the time). He also considered that an "artificial comma" of might be useful, because 31 octaves could be practically approximated by a cycle of 53 just fifths. William Holder, for whom the Holdrian comma is named, favored this latter unit because the intervals of 53 equal temperament are closer to just intonation than that of 55. Thus Mercator's comma and the Holdrian comma are two distinct but related intervals.
Use in Turkish makam theory edit
The Holdrian comma has been employed mainly in Ottoman/Turkish music theory by Kemal Ilerici, and by the Turkish composer Erol Sayan. The name of this comma is Holder koması in Turkish.
| Name of interval | Commas | Cents | Symbol |
|---|---|---|---|
| Koma | 1 | 22.64 | F |
| Bakiye | 4 | 90.57 | B |
| Küçük Mücennep | 5 | 113.21 | S |
| Büyük Mücennep | 8 | 181.13 | K |
| Tanini | 9 | 203.77 | T |
| Artık Aralık (12) | 12 | 271.70 | A (12) |
| Artık Aralık (13) | 13 | 294.34 | A (13) |
For instance, the Rast makam (similar to the Western major scale, or more precisely to the justly-tuned major scale) may be considered in terms of Holdrian commas:
where denotes a Holdrian comma flat,[i] while in contrast, the Nihavend makam (similar to the Western minor scale):
where ♭ denotes a five-comma flat, has medium seconds between d–e♭, e–f, g–a♭, a♭–b♭, and b♭–c′, a medium second being somewhere in between 8 and 9 commas.[13]
Notes edit
- ^ In common Arabic and Turkish practice, the third note e and the seventh note b in Rast are even lower than in this theory, almost exactly halfway between western major and minor thirds above c and g, i.e. closer to 6.5 commas (three-quarter tone) above d or a and 6.5 below f or c, the thirds c–e and g–b often referred to as a "neutral thirds" by musicologists.
References edit
- ^ Milne, Andrew; Sethares, William; Plamondon, James (2007). "Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over a Tuning Continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15. S2CID 27906745.
- ^ McClain, Ernest and Ming Shui Hung. Chinese Cyclic Tunings in Late Antiquity, Ethnomusicology Vol. 23 No. 2, 1979. pp. 205–224.
- ^ "後漢書/卷91 - 维基文库,自由的图书馆". zh.wikisource.org (in Chinese). Retrieved 2022-06-23.
- ^ Monzo, Joe (2005). "Mercator's Comma", Tonalsoft.
- ^ Holder, William, Treatise on the Natural Grounds and Principles of Harmony, facsimile of the 1694 London edition, Broude Brothers, 1967
- ^ Stanley, Jerome, William Holder and His Position in Seventeenth-Century Philosophy and Music Theory, The Edwin Mellen Press, 2002
- ^ Barbieri, Patrizio. Enharmonic instruments and music, 1470–1900 Archived 2009-02-15 at the Wayback Machine. (2008) Latina, Il Levante Libreria Editrice, p. 350.
- ^ a b von Helmholtz, H.L.F. (1954). Ellis, Alexander (ed.). On the Sensations of Tone (second English ed.). Dover Publications. pp. 328–329.
- ^ Slavencki, Josip (21 June 2007). "Preface to 53EDO piece" (manuscript). The Faculty of Music in Belgrade Serbia – via Wikimedia Commons.
- ^ Slavencki, Josip (21 June 2007). "Title with 53EDO movement" (manuscript). The Faculty of Music in Belgrade Serbia – via Wikimedia Commons.
- ^ Slavenski, Josip (February 2018). "Music Natural 53e6v". soundcloud.com.
Croatian composer Josip Štolcer-Slavenski wrote one piece, which has never been published, which uses Bosanquet's Enharmonium during its first movement, entitled Music for Natur-ton-system
- ^ Westbrook, James (2012). "General Thompson's Enharmonic Guitar". Soundboard. Vol. 38, no. 4. pp. 45–52.
- ^ a b c d Habib Hassan Touma (1996). The Music of the Arabs, p.23. trans. Laurie Schwartz. Portland, Oregon: Amadeus Press. ISBN 0-931340-88-8.
- ^ A. M. S. Boethius, De institutione musica, Book 3, Chap. 8. According to Boethius, Pythagoras' disciple Philolaos would have said that the tone consisted in two diatonic semitones and a comma; the diatonic semitone consisted in two diaschismata, each formed of two commas. See J. Murray Barbour, Tuning and Temperament: A Historical Survey, 1951, p. 123
- ^ W. Holder, A Treatise of the Natural Grounds, and Principles of Harmony, London, 3d edition, 1731, p. 79.
- ^ "The late Nicholas Mercator, a Modest Person, and a Learned and Judicious Mathematician, in a Manuscript of his, of which I have had a Sight."
- ^ W. Holder, A Treatise..., ibid., writes that Mersenne had calculated 58¼ commas in the octave; Mercator "working by the Logarithms, finds out but 55, and a little more."
- Holder, William (1967) [1694]. A Treatise on the Natural Grounds, and Principles of Harmony (facsimile ed.). New York, NY: Broude Brothers. pp. 103–106.
External links edit
- Rodgers, Prent (May 2007). "Whisper Song in 53 EDO". Bumper Music (podcast) (slower ed.).
- Hanson, Larry (1989). "Development of a 53 tone keyboard layout" (PDF). Xenharmonicon XII. Hanover, NH: Frog Peak Music: 68–85. Retrieved 2021-01-04 – via Anaphoria.com.
- "Algebra of Tonal Functions". Sonantometry (blog). 2007-05-01. Tonal Functions as 53-TET grades.
- Barbieri, Patrizio (2008). "Enharmonic instruments and music, 1470–1900". Latina, Il Levante Libreria Editrice. Italy. Archived from the original on 2009-02-15.[dead link]
- Kukula, Jim (August 2005). "Equal temperament with 53 pitches per octave". Interdependent Science. Fractal Microtonal Music. Retrieved 2021-01-04.