This article needs additional citations for verification. (March 2019) |
A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. The primary benefit of the circuit is its ability to provide extremely accurate measurements (in contrast with something like a simple voltage divider).[1] Its operation is similar to the original potentiometer.
The Wheatstone bridge was invented by Samuel Hunter Christie (sometimes spelled "Christy") in 1833 and improved and popularized by Sir Charles Wheatstone in 1843.[2] One of the Wheatstone bridge's initial uses was for soil analysis and comparison.[3]
Operation
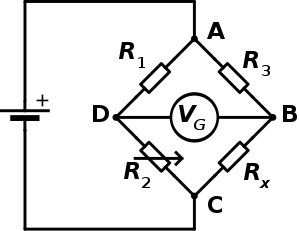
editIn the figure, Rx is the fixed, yet unknown, resistance to be measured. R1, R2, and R3 are resistors of known resistance and the resistance of R2 is adjustable. The resistance R2 is adjusted until the bridge is "balanced" and no current flows through the galvanometer Vg. At this point, the potential difference between the two midpoints (B and D) will be zero. Therefore the ratio of the two resistances in the known leg (R2 / R1) is equal to the ratio of the two resistances in the unknown leg (Rx / R3). If the bridge is unbalanced, the direction of the current indicates whether R2 is too high or too low.
At the point of balance,
Detecting zero current with a galvanometer can be done to extremely high precision. Therefore, if R1, R2, and R3 are known to high precision, then Rx can be measured to high precision. Very small changes in Rx disrupt the balance and are readily detected.
Alternatively, if R1, R2, and R3 are known, but R2 is not adjustable, the voltage difference across or current flow through the meter can be used to calculate the value of Rx, using Kirchhoff's circuit laws. This setup is frequently used in strain gauge and resistance thermometer measurements, as it is usually faster to read a voltage level off a meter than to adjust a resistance to zero the voltage.
Derivation
editQuick derivation at balance
editAt the point of balance, both the voltage and the current between the two midpoints (B and D) are zero. Therefore, I1 = I2, I3 = Ix, VD = VB.
Because of VD = VB, then VDC = VBC and VAD = VAB.
Dividing the last two equations by members and using the above currents equalities, then
Full derivation using Kirchhoff's circuit laws
editFirst, Kirchhoff's first law is used to find the currents in junctions B and D:
Then, Kirchhoff's second law is used for finding the voltage in the loops ABDA and BCDB:
When the bridge is balanced, then IG = 0, so the second set of equations can be rewritten as:
Then, equation (1) is divided by equation (2) and the resulting equation is rearranged, giving:
Due to I3 = Ix and I1 = I2 being proportional from Kirchhoff's First Law, I3I2/I1Ix cancels out of the above equation. The desired value of Rx is now known to be given as:
On the other hand, if the resistance of the galvanometer is high enough that IG is negligible, it is possible to compute Rx from the three other resistor values and the supply voltage (VS), or the supply voltage from all four resistor values. To do so, one has to work out the voltage from each potential divider and subtract one from the other. The equations for this are:
where VG is the voltage of node D relative to node B.
Significance
editThe Wheatstone bridge illustrates the concept of a difference measurement, which can be extremely accurate. Variations on the Wheatstone bridge can be used to measure capacitance, inductance, impedance and other quantities, such as the amount of combustible gases in a sample, with an explosimeter. The Kelvin bridge was specially adapted from the Wheatstone bridge for measuring very low resistances. In many cases, the significance of measuring the unknown resistance is related to measuring the impact of some physical phenomenon (such as force, temperature, pressure, etc.) which thereby allows the use of Wheatstone bridge in measuring those elements indirectly.
The concept was extended to alternating current measurements by James Clerk Maxwell in 1865[4] and further improved as Blumlein bridge by Alan Blumlein in British Patent no. 323,037, 1928.
Modifications of the basic bridge
editThe Wheatstone bridge is the fundamental bridge, but there are other modifications that can be made to measure various kinds of resistances when the fundamental Wheatstone bridge is not suitable. Some of the modifications are:
- Carey Foster bridge, for measuring small resistances
- Kelvin bridge, for measuring small four-terminal resistances
- Maxwell bridge, and Wien bridge for measuring reactive components
- Anderson's bridge, for measuring the self-inductance of the circuit, an advanced form of Maxwell's bridge
See also
edit- Diode bridge, product mixer – diode bridges
- Phantom circuit – a circuit using a balanced bridge
- Post office box (electricity)
- Potentiometer (measuring instrument)
- Potential divider
- Ohmmeter
- Resistance thermometer
- Strain gauge
References
edit- ^ "Circuits in Practice: The Wheatstone Bridge, What It Does, and Why It Matters", as discussed in this MIT ES.333 class video
- ^ Wheatstone, Charles (1843). "XIII. The Bakerian lecture.—An account of several new instruments and processes for determining the constants of a voltaic circuit". Phil. Trans. R. Soc. 133: 303–327. doi:10.1098/rstl.1843.0014.
- ^ Ekelof, Stig (February 2001). "The Genesis of the Wheatstone Bridge" (PDF). Engineering Science and Education Journal. 10 (1): 37–40. doi:10.1049/esej:20010106. discusses Christie's and Wheatstone's contributions, and why the bridge carries Wheatstone's name.
- ^ Maxwell, J. Clerk (1865). "A dynamical theory of the electromagnetic field". Philosophical Transactions of the Royal Society of London. 155: 459–512. Maxwell's bridge used a battery and a ballistic galvanometer. See pp. 475–477.
External links
edit- Media related to Wheatstone's bridge at Wikimedia Commons
- DC Metering Circuits chapter from Lessons In Electric Circuits Vol 1 DC free ebook and Lessons In Electric Circuits series.
- Test Set I-49