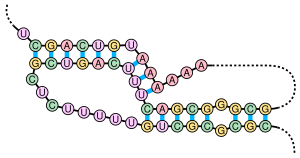

A pseudoknot is a nucleic acid secondary structure containing at least two stem-loop structures in which half of one stem is intercalated between the two halves of another stem. The pseudoknot was first recognized in the turnip yellow mosaic virus in 1982.[2] Pseudoknots fold into knot-shaped three-dimensional conformations but are not true topological knots.
Biological significance
editSeveral important biological processes rely on RNA molecules that form pseudoknots, which are often RNAs with extensive tertiary structure. For example, the pseudoknot region of RNase P is one of the most conserved elements in all of evolution. The telomerase RNA component contains a pseudoknot that is critical for activity,[1] and several viruses use a pseudoknot structure to form a tRNA-like motif to infiltrate the host cell.[3]
Computational aspects
editPseudoknots are significant in the context of bioinformatics, because a large class of important algorithms are incapable of considering secondary structures that include pseudoknots. These algorithms include the Zuker Algorithm to predict a secondary structuree given a single sequence, which is the basis of the Mfold and ViennaRNA software packages, and various algorithms based on stochastic context-free grammars, e.g., covariancee models that are currently highly successful in the context of RNA-specific homology search. Because of this limitation, pseudoknots are often ignored. In cases where pseudoknots are important, more time-consuming algorithms or algorithms based on heuristics that are not guaranteed to perform optimally must be used. However, some algorithms do not intrinsically suffer from a difficulty with pseudoknots.
This algorithmic limitation is more readily apparent in the context of the dot-bracket representation of secondary structure.
Representation of secondary structure and pseudoknots
editMany types of pseudoknots exist, differing by how they cross and how many times they cross. To reflect this difference, pseudoknots are classed into H-, K-, L-, M-types, with each successive type adding a layer of step intercalation. The simple telomerase P2b-P3 example in the article, for example, is an H-type pseudoknot.[4]
RNA secondary structure is usually represented by the dot-bracket notation, with pairing round brackets () indicating basepairs in a stem and dots representing loops. The interrupted stems of pseudoknots mean that such notation must be extended with extra brackets, or even letters, so that different sets of stems can be represented. One such extension uses, in nesting order, ([{<ABCDE for opening and edcba>}]) for closing.[5] The structure for the two (slightly varying) telomerase examples, in this notation, is:
(((.(((((........))))).))). ....]]]]]]. drawing 1 CGCGCGCUGUUUUUCUCGCUGACUUUCAGCGGGCGA---AAAAAAUGUCAGCU 50 ALIGN |.||||||||||||||||||||||||| .|.| |||||| ||||||. 1ymo 1 ---GGGCUGUUUUUCUCGCUGACUUUCAGC--CCCAAACAAAAAA-GUCAGCA 47 ((((((........)))) )).........]]]]]].
Note that U bulge at the end is normally present in telomerase RNA. It was removed in the 1ymo solution model for enhanced stability of the pseudoknot.[6]
Prediction and identification
editThe structural configuration of pseudoknots does not lend itself well to bio-computational detection due to its context-sensitivity or "overlapping" nature. The base pairing in pseudoknots is not well nested; that is, base pairs occur that "overlap" one another in sequence position. This makes the presence of pseudoknots in RNA sequences more difficult to predict by the standard method of dynamic programming, which use a recursive scoring system to identify paired stems and consequently, most cannot detect non-nested base pairs. The newer method of stochastic context-free grammars suffers from the same problem. Thus, popular secondary structure prediction methods like Mfold and Pfold will not predict pseudoknot structures present in a query sequence; they will only identify the more stable of the two pseudoknot stems.
It is possible to identify a limited class of pseudoknots using dynamic programming, but these methods are not exhaustive and scale worse as a function of sequence length than non-pseudoknotted algorithms.[7][8] The general problem of predicting lowest free energy structures with pseudoknots has been shown to be NP-complete.[9][10]
See also
editReferences
edit- ^ a b Chen, JL; Greider, CW (7 June 2005). "Functional analysis of the pseudoknot structure in human telomerase RNA". Proceedings of the National Academy of Sciences of the United States of America. 102 (23): 8077–9. Bibcode:2005PNAS..102.8080C. doi:10.1073/pnas.0502259102. PMC 1149427. PMID 15849264.
- ^ Staple DW, Butcher SE (June 2005). "Pseudoknots: RNA structures with diverse functions". PLOS Biol. 3 (6): e213. doi:10.1371/journal.pbio.0030213. PMC 1149493. PMID 15941360.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - ^ Pleij CW, Rietveld K, Bosch L (1985). "A new principle of RNA folding based on pseudoknotting". Nucleic Acids Res. 13 (5): 1717–31. doi:10.1093/nar/13.5.1717. PMC 341107. PMID 4000943.
- ^ Kucharík, M; Hofacker, IL; Stadler, PF; Qin, J (15 January 2016). "Pseudoknots in RNA folding landscapes". Bioinformatics. 32 (2): 187–94. doi:10.1093/bioinformatics/btv572. PMC 4708108. PMID 26428288.
- ^ Antczak, M; Popenda, M; Zok, T; Zurkowski, M; Adamiak, RW; Szachniuk, M (15 April 2018). "New algorithms to represent complex pseudoknotted RNA structures in dot-bracket notation". Bioinformatics. 34 (8): 1304–1312. doi:10.1093/bioinformatics/btx783. PMC 5905660. PMID 29236971.
- ^ Theimer, CA; Blois, CA; Feigon, J (4 March 2005). "Structure of the human telomerase RNA pseudoknot reveals conserved tertiary interactions essential for function". Molecular Cell. 17 (5): 671–82. doi:10.1016/j.molcel.2005.01.017. PMID 15749017.
- ^ Rivas E, Eddy S. (1999). "A dynamic programming algorithm for RNA structure prediction including pseudoknots". J Mol Biol 285(5): 2053–2068.
- ^ Dirks, R.M. Pierce N.A. (2004) An algorithm for computing nucleic acid base-pairing probabilities including pseudoknots. "J Computation Chemistry". 25:1295-1304, 2004.
- ^ Lyngsø RB, Pedersen CN. (2000). "RNA pseudoknot prediction in energy-based models". J Comput Biol 7(3–4): 409–427.
- ^ Lyngsø, R. B. (2004). Complexity of pseudoknot prediction in simple models. Paper presented at the ICALP.
External links
edit