stuff
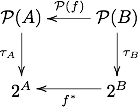
We want to verify the equation

where τC: P(C) → 2C is the map which sends any subset of the set C to the characteristic function on that subset, i.e.

where χU is given by

for any subset U ⊆ C and any element c ∈ C. To verify the equation, let both sides act on some subset S ⊆ B. We have

by the definition of the powerset functor, and so

On the right-hand side of the equation, we have

and recall that f* is the pullback by f induced by the contravariant hom-functor; it acts on maps by multiplication on the right:

So it remains to check the equality

To verify this equation, act both maps in 2A on an arbitrary element a ∈ A.


Since a ∈ f–1(S) iff f(a) ∈ S, these maps are equal.
- probably cornbread










