In number theory, a superior highly composite number is a natural number which, in a particular rigorous sense, has many divisors. Particularly, it is defined by a ratio between the number of divisors an integer has and that integer raised to some positive power.
For any possible exponent, whichever integer has the greatest ratio is a superior highly composite number. It is a stronger restriction than that of a highly composite number, which is defined as having more divisors than any smaller positive integer.
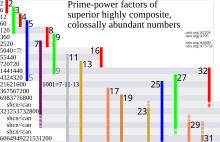
The first ten superior highly composite numbers and their factorization are listed.
| # prime factors |
SHCN n |
Prime factorization |
Prime exponents |
# divisors d(n) |
Primorial factorization |
|---|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 2 | 2 |
| 2 | 6 | 2 ⋅ 3 | 1,1 | 4 | 6 |
| 3 | 12 | 22 ⋅ 3 | 2,1 | 6 | 2 ⋅ 6 |
| 4 | 60 | 22 ⋅ 3 ⋅ 5 | 2,1,1 | 12 | 2 ⋅ 30 |
| 5 | 120 | 23 ⋅ 3 ⋅ 5 | 3,1,1 | 16 | 22 ⋅ 30 |
| 6 | 360 | 23 ⋅ 32 ⋅ 5 | 3,2,1 | 24 | 2 ⋅ 6 ⋅ 30 |
| 7 | 2520 | 23 ⋅ 32 ⋅ 5 ⋅ 7 | 3,2,1,1 | 48 | 2 ⋅ 6 ⋅ 210 |
| 8 | 5040 | 24 ⋅ 32 ⋅ 5 ⋅ 7 | 4,2,1,1 | 60 | 22 ⋅ 6 ⋅ 210 |
| 9 | 55440 | 24 ⋅ 32 ⋅ 5 ⋅ 7 ⋅ 11 | 4,2,1,1,1 | 120 | 22 ⋅ 6 ⋅ 2310 |
| 10 | 720720 | 24 ⋅ 32 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 13 | 4,2,1,1,1,1 | 240 | 22 ⋅ 6 ⋅ 30030 |

For a superior highly composite number n there exists a positive real number ε > 0 such that for all natural numbers k > 1 we have
For example, the number with the most divisors per square root of the number itself is 12; this can be demonstrated using some highly composites near 12.
120 is another superior highly composite number because it has the highest ratio of divisors to itself raised to the .4 power.
The first 15 superior highly composite numbers, 2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 (sequence A002201 in the OEIS) are also the first 15 colossally abundant numbers, which meet a similar condition based on the sum-of-divisors function rather than the number of divisors. Neither set, however, is a subset of the other.
Properties edit
All superior highly composite numbers are highly composite. This is easy to prove: if there is some number k that has the same number of divisors as n but is less than n itself (i.e. , but ), then for all positive ε, so if a number "n" is not highly composite, it cannot be superior highly composite.
An effective construction of the set of all superior highly composite numbers is given by the following monotonic mapping from the positive real numbers.[2] Let
Note that the product need not be computed indefinitely, because if then , so the product to calculate can be terminated once .
Also note that in the definition of , is analogous to in the implicit definition of a superior highly composite number.
Moreover, for each superior highly composite number exists a half-open interval such that .
This representation implies that there exist an infinite sequence of such that for the n-th superior highly composite number holds
The first are 2, 3, 2, 5, 2, 3, 7, ... (sequence A000705 in the OEIS). In other words, the quotient of two successive superior highly composite numbers is a prime number.
Radices edit
The first few superior highly composite numbers have often been used as radices, due to their high divisibility for their size. For example:
- Binary (base 2)
- Senary (base 6)
- Duodecimal (base 12)
- Sexagesimal (base 60)
Bigger SHCNs can be used in other ways. 120 appears as the long hundred, while 360 appears as the number of degrees in a circle.
Notes edit
- ^ Weisstein, Eric W. "Superior Highly Composite Number". mathworld.wolfram.com. Retrieved 2021-03-05.
- ^ Ramanujan (1915); see also URL http://wwwhomes.uni-bielefeld.de/achim/hcn.dvi
References edit
- Ramanujan, S. (1915). "Highly composite numbers". Proc. London Math. Soc. Series 2. 14: 347–409. doi:10.1112/plms/s2_14.1.347. JFM 45.1248.01. Reprinted in Collected Papers (Ed. G. H. Hardy et al.), New York: Chelsea, pp. 78–129, 1962
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. pp. 45–46. ISBN 1-4020-4215-9. Zbl 1151.11300.


