| Stellated octahedron | |
|---|---|
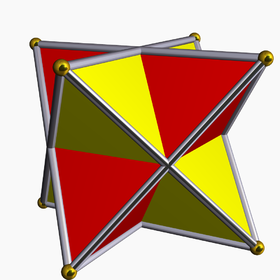 Seen as a compound of two regular tetrahedra (red and yellow) | |
| Type | Regular compound |
| Coxeter symbol | {4,3}[2{3,3}]{3,4}[1] |
| Schläfli symbols | {{3,3}} a{4,3} ß{2,4} ßr{2,2} |
| Coxeter diagrams | |
| Stellation core | Octahedron |
| Convex hull | Cube |
| Index | UC4, W19 |
| Polyhedra | 2 tetrahedra |
| Faces | 8 triangles |
| Edges | 12 |
| Vertices | 8 |
| Dual | Self-dual |
| Symmetry group Coxeter group |
Oh, [4,3], order 48 D4h, [4,2], order 16 D2h, [2,2], order 8 D3d, [2+,6], order 12 |
| Subgroup restricting to one constituent |
Td, [3,3], order 24 D2d, [2+,4], order 8 D2, [2,2]+, order 4 C3v, [3], order 6 |
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's De Divina Proportione, 1509.[2]

It is the simplest of five regular polyhedral compounds, and the only regular compound of two tetrahedra. It is also the least dense of the regular polyhedral compounds, having a density of 2.
It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. It can also be seen as one of the stages in the construction of a 3D Koch snowflake, a fractal shape formed by repeated attachment of smaller tetrahedra to each triangular face of a larger figure. The first stage of the construction of the Koch Snowflake is a single central tetrahedron, and the second stage, formed by adding four smaller tetrahedra to the faces of the central tetrahedron, is the stellated octahedron.
Construction edit
The Cartesian coordinates of the stellated octahedron are as follows:
The stellated octahedron can be constructed in several ways:
- It is a stellation of the regular octahedron, sharing the same face planes. (See Wenninger model W19.)
| In perspective |
Stellation plane |
The only stellation of a regular octahedron, with one stellation plane in yellow. |
- It is also a regular polyhedron compound, when constructed as the union of two regular tetrahedra (a regular tetrahedron and its dual tetrahedron).
- It can be obtained as an augmentation of the regular octahedron, by adding tetrahedral pyramids on each face. In this construction it has the same topology as the convex Catalan solid, the triakis octahedron, which has much shorter pyramids.
- It is a facetting of the cube, sharing the vertex arrangement.
- It can be seen as a {4/2} antiprism; with {4/2} being a tetragram, a compound of two dual digons, and the tetrahedron seen as a digonal antiprism, this can be seen as a compound of two digonal antiprisms.
- It can be seen as a net of a four-dimensional octahedral pyramid, consisting of a central octahedron surrounded by eight tetrahedra.
| Facetting of a cube |
A single diagonal triangle facetting in red |
Related concepts edit
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, where each edge of one tetrahedron crosses the parallel edge of the other tetrahedron. These two tetrahedra can be completed to a desmic system of three tetrahedra, where the third tetrahedron has as its four vertices the three crossing points at infinity and the centroid of the two finite tetrahedra. The same twelve tetrahedron vertices also form the points of Reye's configuration.
The stella octangula numbers are figurate numbers that count the number of balls that can be arranged into the shape of a stellated octahedron. They are
In popular culture edit
The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print "Stars",[3] and provides the central form in Escher's Double Planetoid (1949).[4]
The obelisk in the center of the Plaza de Europa in Zaragoza, Spain, is surrounded by twelve stellated octahedral lampposts, shaped to form a three-dimensional version of the Flag of Europe.[5]
Some modern mystics have associated this shape with the "merkaba",[6] which according to them is a "counter-rotating energy field" named from an ancient Egyptian word.[7] However, the word "merkaba" is actually Hebrew, and more properly refers to a chariot in the visions of Ezekiel.[8] The resemblance between this shape and the two-dimensional star of David has also been frequently noted.[9]
The musical project, spearheaded by Tally Hall member Joe Hawley along with bandmate Ross Federman and honorary bandmate Bora Karaca, "Miracle Musical" (often stylized in its original Japanese title ミラクルミュージカル, pronounced "mi-ra-ku-ru myu-ji-ka-ru"[10]) makes multiple references towards the stellated octahedron as the stella octangula. The shape is shown on the main website of the project, as well as the merchandise store. [10][11] The third song on their first and only studio album, "Hawaii: Part II", "Black Rainbows" features a lyric sung by Madi Diaz which simply says "Stella octangula".[12]
References edit
- ^ H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
- ^ Barnes, John (2009), "Shapes and Solids", Gems of Geometry, Springer, pp. 25–56, doi:10.1007/978-3-642-05092-3_2, ISBN 978-3-642-05091-6.
- ^ Hart, George W. (1996), "The Polyhedra of M.C. Escher", Virtual Polyhedra.
- ^ Coxeter, H. S. M. (1985), "A special book review: M. C. Escher: His life and complete graphic work", The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010, S2CID 189887063. See in particular p. 61.
- ^ "Obelisco" [Obelisk], Zaragoza es Cultura (in Spanish), Ayuntamiento de Zaragoza, retrieved 2021-10-19
- ^ Dannelley, Richard (1995), Sedona: Beyond the Vortex: Activating the Planetary Ascension Program with Sacred Geometry, the Vortex, and the Merkaba, Light Technology Publishing, p. 14, ISBN 9781622336708
- ^ Melchizedek, Drunvalo (2000), The Ancient Secret of the Flower of Life: An Edited Transcript of the Flower of Life Workshop Presented Live to Mother Earth from 1985 to 1994 -, Volume 1, Light Technology Publishing, p. 4, ISBN 9781891824173
- ^ Patzia, Arthur G.; Petrotta, Anthony J. (2010), Pocket Dictionary of Biblical Studies: Over 300 Terms Clearly & Concisely Defined, The IVP Pocket Reference Series, InterVarsity Press, p. 78, ISBN 9780830867028
- ^ Brisson, David W. (1978), Hypergraphics: visualizing complex relationships in art, science, and technology, Westview Press for the American Association for the Advancement of Science, p. 220,
The Stella octangula is the 3-d analog of the Star of David
- ^ a b "ミラクルミュージカル". ミラクルミュージカル. Retrieved 2024-03-09.
- ^ "Miracle Musical Store". Miracle Musical. Retrieved 2024-03-09.
- ^ Miracle Musical (Ft. Joe Hawley & Madi Diaz) – Black Rainbows, retrieved 2024-03-09
External links edit
- Weisstein, Eric W., "Stella Octangula" ("Compound of two tetrahedra") at MathWorld.
- Klitzing, Richard, "3D compound"