Steiner conic

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.

1. Definition of the Steiner generation of a conic section

The usual definition of a conic uses a quadratic form (see Quadric (projective geometry)). Another alternative definition of a conic uses a hyperbolic polarity. It is due to K. G. C. von Staudt and sometimes called a von Staudt conic. The disadvantage of von Staudt's definition is that it only works when the underlying field has odd characteristic (i.e., $Char\neq 2$).

Definition of a Steiner conic

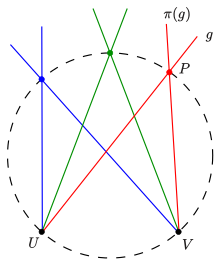
• Given two pencils $B(U),B(V)$ of lines at two points $U,V$ (all lines containing $U$ and $V$ resp.) and a projective but not perspective mapping $\pi$ of $B(U)$ onto $B(V)$. Then the intersection points of corresponding lines form a non-degenerate projective conic section (figure 1)

2. Perspective mapping between lines

A perspective mapping $\pi$ of a pencil $B(U)$ onto a pencil $B(V)$ is a bijection (1-1 correspondence) such that corresponding lines intersect on a fixed line $a$, which is called the axis of the perspectivity $\pi$ (figure 2).

A projective mapping is a finite product of perspective mappings.

Simple example: If one shifts in the first diagram point $U$ and its pencil of lines onto $V$ and rotates the shifted pencil around $V$ by a fixed angle $\varphi$ then the shift (translation) and the rotation generate a projective mapping $\pi$ of the pencil at point $U$ onto the pencil at $V$. From the inscribed angle theorem one gets: The intersection points of corresponding lines form a circle.

Examples of commonly used fields are the real numbers $\mathbb {R}$, the rational numbers $\mathbb {Q}$ or the complex numbers $\mathbb {C}$. The construction also works over finite fields, providing examples in finite projective planes.

Remark: The fundamental theorem for projective planes states, that a projective mapping in a projective plane over a field (pappian plane) is uniquely determined by prescribing the images of three lines. That means that, for the Steiner generation of a conic section, besides two points $U,V$ only the images of 3 lines have to be given. These 5 items (2 points, 3 lines) uniquely determine the conic section.

Remark: The notation "perspective" is due to the dual statement: The projection of the points on a line $a$ from a center $Z$ onto a line $b$ is called a perspectivity (see below).

3. Example of a Steiner generation: generation of a point

Example

For the following example the images of the lines $a,u,w$ (see picture) are given: $\pi (a)=b,\pi (u)=w,\pi (w)=v$. The projective mapping $\pi$ is the product of the following perspective mappings $\pi _{b},\pi _{a}$: 1) $\pi _{b}$ is the perspective mapping of the pencil at point $U$ onto the pencil at point $O$ with axis $b$. 2) $\pi _{a}$ is the perspective mapping of the pencil at point $O$ onto the pencil at point $V$ with axis $a$. First one should check that $\pi =\pi _{a}\pi _{b}$ has the properties: $\pi (a)=b,\pi (u)=w,\pi (w)=v$. Hence for any line $g$ the image $\pi (g)=\pi _{a}\pi _{b}(g)$ can be constructed and therefore the images of an arbitrary set of points. The lines $u$ and $v$ contain only the conic points $U$ and $V$ resp.. Hence $u$ and $v$ are tangent lines of the generated conic section.

A proof that this method generates a conic section follows from switching to the affine restriction with line $w$ as the line at infinity, point $O$ as the origin of a coordinate system with points $U,V$ as points at infinity of the x- and y-axis resp. and point $E=(1,1)$. The affine part of the generated curve appears to be the hyperbola $y=1/x$.

Remark:

1. The Steiner generation of a conic section provides simple methods for the construction of ellipses, parabolas and hyperbolas which are commonly called the parallelogram methods.
2. The figure that appears while constructing a point (figure 3) is the 4-point-degeneration of Pascal's theorem.

Steiner generation of a dual conic

dual ellipse

Steiner generation of a dual conic

definition of a perspective mapping

Definitions and the dual generation

Dualizing (see duality (projective geometry)) a projective plane means exchanging the points with the lines and the operations intersection and connecting. The dual structure of a projective plane is also a projective plane. The dual plane of a pappian plane is pappian and can also be coordinatized by homogeneous coordinates. A nondegenerate dual conic section is analogously defined by a quadratic form.

A dual conic can be generated by Steiner's dual method:

• Given the point sets of two lines $u,v$ and a projective but not perspective mapping $\pi$ of $u$ onto $v$. Then the lines connecting corresponding points form a dual non-degenerate projective conic section.

A perspective mapping $\pi$ of the point set of a line $u$ onto the point set of a line $v$ is a bijection (1-1 correspondence) such that the connecting lines of corresponding points intersect at a fixed point $Z$, which is called the centre of the perspectivity $\pi$ (see figure).

A projective mapping is a finite sequence of perspective mappings.

It is usual, when dealing with dual and common conic sections, to call the common conic section a point conic and the dual conic a line conic.

In the case that the underlying field has $\operatorname {Char} =2$ all the tangents of a point conic intersect in a point, called the knot (or nucleus) of the conic. Thus, the dual of a non-degenerate point conic is a subset of points of a dual line and not an oval curve (in the dual plane). So, only in the case that $\operatorname {Char} \neq 2$ is the dual of a non-degenerate point conic a non-degenerate line conic.

Examples

Dual Steiner conic defined by two perspectivities $\pi _{A},\pi _{B}$

example of a Steiner generation of a dual conic

(1) Projectivity given by two perspectivities:
Two lines $u,v$ with intersection point $W$ are given and a projectivity $\pi$ from $u$ onto $v$ by two perspectivities $\pi _{A},\pi _{B}$ with centers $A,B$. $\pi _{A}$ maps line $u$ onto a third line $o$, $\pi _{B}$ maps line $o$ onto line $v$ (see diagram). Point $W$ must not lie on the lines ${\overline {AB}},o$. Projectivity $\pi$ is the composition of the two perspectivities: $\ \pi =\pi _{B}\pi _{A}$. Hence a point $X$ is mapped onto $\pi (X)=\pi _{B}\pi _{A}(X)$ and the line $x={\overline {X\pi (X)}}$ is an element of the dual conic defined by $\pi$.
(If $W$ would be a fixpoint, $\pi$ would be perspective.)

(2) Three points and their images are given:
The following example is the dual one given above for a Steiner conic.
The images of the points $A,U,W$ are given: $\pi (A)=B,\,\pi (U)=W,\,\pi (W)=V$. The projective mapping $\pi$ can be represented by the product of the following perspectivities $\pi _{B},\pi _{A}$:

1. $\pi _{B}$ is the perspectivity of the point set of line $u$ onto the point set of line $o$ with centre $B$.
2. $\pi _{A}$ is the perspectivity of the point set of line $o$ onto the point set of line $v$ with centre $A$.

One easily checks that the projective mapping $\pi =\pi _{A}\pi _{B}$ fulfills $\pi (A)=B,\,\pi (U)=W,\,\pi (W)=V$. Hence for any arbitrary point $G$ the image $\pi (G)=\pi _{A}\pi _{B}(G)$ can be constructed and line ${\overline {G\pi (G)}}$ is an element of a non degenerate dual conic section. Because the points $U$ and $V$ are contained in the lines $u$, $v$ resp.,the points $U$ and $V$ are points of the conic and the lines $u,v$ are tangents at $U,V$.

Intrinsic conics in a linear incidence geometry

The Steiner construction defines the conics in a planar linear incidence geometry (two points determine at most one line and two lines intersect in at most one point) intrinsically, that is, using only the collineation group. Specifically, $E(T,P)$ is the conic at point $P$ afforded by the collineation $T$, consisting of the intersections of $L$ and $T(L)$ for all lines $L$ through $P$. If $T(P)=P$ or $T(L)=L$ for some $L$ then the conic is degenerate. For example, in the real coordinate plane, the affine type (ellipse, parabola, hyperbola) of $E(T,P)$ is determined by the trace and determinant of the matrix component of $T$, independent of $P$.

By contrast, the collineation group of the real hyperbolic plane $\mathbb {H} ^{2}$consists of isometries. Consequently, the intrinsic conics comprise a small but varied subset of the general conics, curves obtained from the intersections of projective conics with a hyperbolic domain. Further, unlike the Euclidean plane, there is no overlap between the direct $E(T,P);$ $T$ preserves orientation – and the opposite $E(T,P);$ $T$ reverses orientation. The direct case includes central (two perpendicular lines of symmetry) and non-central conics, whereas every opposite conic is central. Even though direct and opposite central conics cannot be congruent, they are related by a quasi-symmetry defined in terms of complementary angles of parallelism. Thus, in any inversive model of $\mathbb {H} ^{2}$, each direct central conic is birationally equivalent to an opposite central conic. In fact, the central conics represent all genus 1 curves with real shape invariant $j\geq 1$. A minimal set of representatives is obtained from the central direct conics with common center and axis of symmetry, whereby the shape invariant is a function of the eccentricity, defined in terms of the distance between $P$ and $T(P)$. The orthogonal trajectories of these curves represent all genus 1 curves with $j\leq 1$, which manifest as either irreducible cubics or bi-circular quartics. Using the elliptic curve addition law on each trajectory, every general central conic in $\mathbb {H} ^{2}$decomposes uniquely as the sum of two intrinsic conics by adding pairs of points where the conics intersect each trajectory.

References

• Coxeter, H. S. M. (1993), The Real Projective Plane, Springer Science & Business Media
• Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF), retrieved 20 September 2014 (PDF; 891 kB).
• Merserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry, Dover, ISBN 0-486-63415-9