Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science statistics,[1][2][3] and is particularly problematic when frequency data are unduly given causal interpretations.[4] The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the statistical modeling[4][5] (e.g., through cluster analysis[6]).
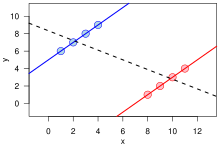

Simpson's paradox has been used to illustrate the kind of misleading results that the misuse of statistics can generate.[7][8]
Edward H. Simpson first described this phenomenon in a technical paper in 1951,[9] but the statisticians Karl Pearson (in 1899[10]) and Udny Yule (in 1903[11]) had mentioned similar effects earlier. The name Simpson's paradox was introduced by Colin R. Blyth in 1972.[12] It is also referred to as Simpson's reversal, the Yule–Simpson effect, the amalgamation paradox, or the reversal paradox.[13]
Mathematician Jordan Ellenberg argues that Simpson's paradox is misnamed as "there's no contradiction involved, just two different ways to think about the same data" and suggests that its lesson "isn't really to tell us which viewpoint to take but to insist that we keep both the parts and the whole in mind at once."[14]
Examples edit
UC Berkeley gender bias edit
One of the best-known examples of Simpson's paradox comes from a study of gender bias among graduate school admissions to University of California, Berkeley. The admission figures for the fall of 1973 showed that men applying were more likely than women to be admitted, and the difference was so large that it was unlikely to be due to chance.[15][16]
| All | Men | Women | ||||
|---|---|---|---|---|---|---|
| Applicants | Admitted | Applicants | Admitted | Applicants | Admitted | |
| Total | 12,763 | 41% | 8,442 | 44% | 4,321 | 35% |
However, when taking into account the information about departments being applied to, the different rejection percentages reveal the different difficulty of getting into the department, and at the same time it showed that women tended to apply to more competitive departments with lower rates of admission, even among qualified applicants (such as in the English department), whereas men tended to apply to less competitive departments with higher rates of admission (such as in the engineering department). The pooled and corrected data showed a "small but statistically significant bias in favor of women".[16]
The data from the six largest departments are listed below:
| Department | All | Men | Women | |||
|---|---|---|---|---|---|---|
| Applicants | Admitted | Applicants | Admitted | Applicants | Admitted | |
| A | 933 | 64% | 825 | 62% | 108 | 82% |
| B | 585 | 63% | 560 | 63% | 25 | 68% |
| C | 918 | 35% | 325 | 37% | 593 | 34% |
| D | 792 | 34% | 417 | 33% | 375 | 35% |
| E | 584 | 25% | 191 | 28% | 393 | 24% |
| F | 714 | 6% | 373 | 6% | 341 | 7% |
| Total | 4526 | 39% | 2691 | 45% | 1835 | 30% |
|
Legend: greater percentage of successful applicants than the other gender
greater number of applicants than the other gender
bold - the two 'most applied for' departments for each gender | ||||||
The entire data showed total of 4 out of 85 departments to be significantly biased against women, while 6 to be significantly biased against men (not all present in the 'six largest departments' table above). Notably, the numbers of biased departments were not the basis for the conclusion, but rather it was the gender admissions pooled across all departments, while weighing by each department's rejection rate across all of its applicants.[16]
Kidney stone treatment edit
Another example comes from a real-life medical study[17] comparing the success rates of two treatments for kidney stones.[18] The table below shows the success rates (the term success rate here actually means the success proportion) and numbers of treatments for treatments involving both small and large kidney stones, where Treatment A includes open surgical procedures and Treatment B includes closed surgical procedures. The numbers in parentheses indicate the number of success cases over the total size of the group.
Treatment Stone size
|
Treatment A | Treatment B |
|---|---|---|
| Small stones | Group 1 93% (81/87) |
Group 2 87% (234/270) |
| Large stones | Group 3 73% (192/263) |
Group 4 69% (55/80) |
| Both | 78% (273/350) | 83% (289/350) |
The paradoxical conclusion is that treatment A is more effective when used on small stones, and also when used on large stones, yet treatment B appears to be more effective when considering both sizes at the same time. In this example, the "lurking" variable (or confounding variable) causing the paradox is the size of the stones, which was not previously known to researchers to be important until its effects were included.[citation needed]
Which treatment is considered better is determined by which success ratio (successes/total) is larger. The reversal of the inequality between the two ratios when considering the combined data, which creates Simpson's paradox, happens because two effects occur together:[citation needed]
- The sizes of the groups, which are combined when the lurking variable is ignored, are very different. Doctors tend to give cases with large stones the better treatment A, and the cases with small stones the inferior treatment B. Therefore, the totals are dominated by groups 3 and 2, and not by the two much smaller groups 1 and 4.
- The lurking variable, stone size, has a large effect on the ratios; i.e., the success rate is more strongly influenced by the severity of the case than by the choice of treatment. Therefore, the group of patients with large stones using treatment A (group 3) does worse than the group with small stones, even if the latter used the inferior treatment B (group 2).
Based on these effects, the paradoxical result is seen to arise because the effect of the size of the stones overwhelms the benefits of the better treatment (A). In short, the less effective treatment B appeared to be more effective because it was applied more frequently to the small stones cases, which were easier to treat.[18]
Batting averages edit
A common example of Simpson's paradox involves the batting averages of players in professional baseball. It is possible for one player to have a higher batting average than another player each year for a number of years, but to have a lower batting average across all of those years. This phenomenon can occur when there are large differences in the number of at bats between the years. Mathematician Ken Ross demonstrated this using the batting average of two baseball players, Derek Jeter and David Justice, during the years 1995 and 1996:[19][20]
Year Batter
|
1995 | 1996 | Combined | |||
|---|---|---|---|---|---|---|
| Derek Jeter | 12/48 | .250 | 183/582 | .314 | 195/630 | .310 |
| David Justice | 104/411 | .253 | 45/140 | .321 | 149/551 | .270 |
In both 1995 and 1996, Justice had a higher batting average (in bold type) than Jeter did. However, when the two baseball seasons are combined, Jeter shows a higher batting average than Justice. According to Ross, this phenomenon would be observed about once per year among the possible pairs of players.[19]
Vector interpretation edit
Simpson's paradox can also be illustrated using a 2-dimensional vector space.[21] A success rate of (i.e., successes/attempts) can be represented by a vector , with a slope of . A steeper vector then represents a greater success rate. If two rates and are combined, as in the examples given above, the result can be represented by the sum of the vectors and , which according to the parallelogram rule is the vector , with slope .
Simpson's paradox says that even if a vector (in orange in figure) has a smaller slope than another vector (in blue), and has a smaller slope than , the sum of the two vectors can potentially still have a larger slope than the sum of the two vectors , as shown in the example. For this to occur one of the orange vectors must have a greater slope than one of the blue vectors (here and ), and these will generally be longer than the alternatively subscripted vectors – thereby dominating the overall comparison.
Correlation between variables edit
Simpson's reversal can also arise in correlations, in which two variables appear to have (say) a positive correlation towards one another, when in fact they have a negative correlation, the reversal having been brought about by a "lurking" confounder. Berman et al.[22] give an example from economics, where a dataset suggests overall demand is positively correlated with price (that is, higher prices lead to more demand), in contradiction of expectation. Analysis reveals time to be the confounding variable: plotting both price and demand against time reveals the expected negative correlation over various periods, which then reverses to become positive if the influence of time is ignored by simply plotting demand against price.
Psychology edit
Psychological interest in Simpson's paradox seeks to explain why people deem sign reversal to be impossible at first. The question is where people get this strong intuition from, and how it is encoded in the mind.
Simpson's paradox demonstrates that this intuition cannot be derived from either classical logic or probability calculus alone, and thus led philosophers to speculate that it is supported by an innate causal logic that guides people in reasoning about actions and their consequences.[4] Savage's sure-thing principle[12] is an example of what such logic may entail. A qualified version of Savage's sure thing principle can indeed be derived from Pearl's do-calculus[4] and reads: "An action A that increases the probability of an event B in each subpopulation Ci of C must also increase the probability of B in the population as a whole, provided that the action does not change the distribution of the subpopulations." This suggests that knowledge about actions and consequences is stored in a form resembling Causal Bayesian Networks.
Probability edit
A paper by Pavlides and Perlman presents a proof, due to Hadjicostas, that in a random 2 × 2 × 2 table with uniform distribution, Simpson's paradox will occur with a probability of exactly 1⁄60.[23] A study by Kock suggests that the probability that Simpson's paradox would occur at random in path models (i.e., models generated by path analysis) with two predictors and one criterion variable is approximately 12.8 percent; slightly higher than 1 occurrence per 8 path models.[24]
Simpson's second paradox edit
A second, less well-known paradox was also discussed in Simpson's 1951 paper. It can occur when the "sensible interpretation" is not necessarily found in the separated data, like in the Kidney Stone example, but can instead reside in the combined data. Whether the partitioned or combined form of the data should be used hinges on the process giving rise to the data, meaning the correct interpretation of the data cannot always be determined by simply observing the tables.[25]
Judea Pearl has shown that, in order for the partitioned data to represent the correct causal relationships between any two variables, and , the partitioning variables must satisfy a graphical condition called "back-door criterion":[26][27]
- They must block all spurious paths between and
- No variable can be affected by
This criterion provides an algorithmic solution to Simpson's second paradox, and explains why the correct interpretation cannot be determined by data alone; two different graphs, both compatible with the data, may dictate two different back-door criteria.
When the back-door criterion is satisfied by a set Z of covariates, the adjustment formula (see Confounding) gives the correct causal effect of X on Y. If no such set exists, Pearl's do-calculus can be invoked to discover other ways of estimating the causal effect.[4][28] The completeness of do-calculus [29][28] can be viewed as offering a complete resolution of the Simpson's paradox.
Criticism edit
One criticism is that the paradox is not really a paradox at all, but rather a failure to properly account for confounding variables or to consider causal relationships between variables.[30]
Another criticism of the apparent Simpson's paradox is that it may be a result of the specific way that data is stratified or grouped. The phenomenon may disappear or even reverse if the data is stratified differently or if different confounding variables are considered. Simpson's example actually highlighted a phenomenon called noncollapsibility,[31] which occurs when subgroups with high proportions do not make simple averages when combined. This suggests that the paradox may not be a universal phenomenon, but rather a specific instance of a more general statistical issue.
Critics of the apparent Simpson's paradox also argue that the focus on the paradox may distract from more important statistical issues, such as the need for careful consideration of confounding variables and causal relationships when interpreting data.[32]
Despite these criticisms, the apparent Simpson's paradox remains a popular and intriguing topic in statistics and data analysis. It continues to be studied and debated by researchers and practitioners in a wide range of fields, and it serves as a valuable reminder of the importance of careful statistical analysis and the potential pitfalls of simplistic interpretations of data.
See also edit
- Aliasing – Signal processing effect
- Anscombe's quartet – Four data sets with the same descriptive statistics, yet very different distributions
- Berkson's paradox – Tendency to misinterpret statistical experiments involving conditional probabilities
- Cherry picking – Fallacy of incomplete evidence
- Condorcet paradox – Self-contradiction of majority rule
- Ecological fallacy – Logical fallacy that occurs when group characteristics are applied to individuals
- Gerrymandering – Form of political manipulation
- Low birth-weight paradox – Statistical quirk of babies' birth weights
- Modifiable areal unit problem – Source of statistical bias
- Prosecutor's fallacy – Error in thinking which involves under-valuing base rate information
- Will Rogers phenomenon – Statistical phenomenon and paradox
- Spurious correlation
- Omitted-variable bias
References edit
- ^ Clifford H. Wagner (February 1982). "Simpson's Paradox in Real Life". The American Statistician. 36 (1): 46–48. doi:10.2307/2684093. JSTOR 2684093.
- ^ Holt, G. B. (2016). Potential Simpson's paradox in multicenter study of intraperitoneal chemotherapy for ovarian cancer. Journal of Clinical Oncology, 34(9), 1016–1016.
- ^ Franks, Alexander; Airoldi, Edoardo; Slavov, Nikolai (2017). "Post-transcriptional regulation across human tissues". PLOS Computational Biology. 13 (5): e1005535. arXiv:1506.00219. Bibcode:2017PLSCB..13E5535F. doi:10.1371/journal.pcbi.1005535. ISSN 1553-7358. PMC 5440056. PMID 28481885.
- ^ a b c d e Judea Pearl. Causality: Models, Reasoning, and Inference, Cambridge University Press (2000, 2nd edition 2009). ISBN 0-521-77362-8.
- ^ Kock, N., & Gaskins, L. (2016). Simpson's paradox, moderation and the emergence of quadratic relationships in path models: An information systems illustration. International Journal of Applied Nonlinear Science, 2(3), 200–234.
- ^ Rogier A. Kievit, Willem E. Frankenhuis, Lourens J. Waldorp and Denny Borsboom, Simpson's paradox in psychological science: a practical guide https://doi.org/10.3389/fpsyg.2013.00513
- ^ Robert L. Wardrop (February 1995). "Simpson's Paradox and the Hot Hand in Basketball". The American Statistician, 49 (1): pp. 24–28.
- ^ Alan Agresti (2002). "Categorical Data Analysis" (Second edition). John Wiley and Sons ISBN 0-471-36093-7
- ^ Simpson, Edward H. (1951). "The Interpretation of Interaction in Contingency Tables". Journal of the Royal Statistical Society, Series B. 13: 238–241.
- ^ Pearson, Karl; Lee, Alice; Bramley-Moore, Lesley (1899). "Genetic (reproductive) selection: Inheritance of fertility in man, and of fecundity in thoroughbred racehorses". Philosophical Transactions of the Royal Society A. 192: 257–330. doi:10.1098/rsta.1899.0006.
- ^ G. U. Yule (1903). "Notes on the Theory of Association of Attributes in Statistics". Biometrika. 2 (2): 121–134. doi:10.1093/biomet/2.2.121.
- ^ a b Colin R. Blyth (June 1972). "On Simpson's Paradox and the Sure-Thing Principle". Journal of the American Statistical Association. 67 (338): 364–366. doi:10.2307/2284382. JSTOR 2284382.
- ^ I. J. Good, Y. Mittal (June 1987). "The Amalgamation and Geometry of Two-by-Two Contingency Tables". The Annals of Statistics. 15 (2): 694–711. doi:10.1214/aos/1176350369. ISSN 0090-5364. JSTOR 2241334.
- ^ Ellenberg, Jordan (May 25, 2021). Shape: The Hidden Geometry of Information, Biology, Strategy, Democracy and Everything Else. New York: Penguin Press. p. 228. ISBN 978-1-9848-7905-9. OCLC 1226171979.
- ^ David Freedman, Robert Pisani, and Roger Purves (2007), Statistics (4th edition), W. W. Norton. ISBN 0-393-92972-8.
- ^ a b c P.J. Bickel, E.A. Hammel and J.W. O'Connell (1975). "Sex Bias in Graduate Admissions: Data From Berkeley" (PDF). Science. 187 (4175): 398–404. Bibcode:1975Sci...187..398B. doi:10.1126/science.187.4175.398. PMID 17835295. S2CID 15278703. Archived (PDF) from the original on 2016-06-04.
- ^ C. R. Charig; D. R. Webb; S. R. Payne; J. E. Wickham (29 March 1986). "Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extracorporeal shockwave lithotripsy". Br Med J (Clin Res Ed). 292 (6524): 879–882. doi:10.1136/bmj.292.6524.879. PMC 1339981. PMID 3083922.
- ^ a b Steven A. Julious; Mark A. Mullee (3 December 1994). "Confounding and Simpson's paradox". BMJ. 309 (6967): 1480–1481. doi:10.1136/bmj.309.6967.1480. PMC 2541623. PMID 7804052.
- ^ a b Ken Ross. "A Mathematician at the Ballpark: Odds and Probabilities for Baseball Fans (Paperback)" Pi Press, 2004. ISBN 0-13-147990-3. 12–13
- ^ Statistics available from Baseball-Reference.com: Data for Derek Jeter; Data for David Justice.
- ^ Kocik Jerzy (2001). "Proofs without Words: Simpson's Paradox" (PDF). Mathematics Magazine. 74 (5): 399. doi:10.2307/2691038. JSTOR 2691038. Archived (PDF) from the original on 2010-06-12.
- ^ Berman, S. DalleMule, L. Greene, M., Lucker, J. (2012), "Simpson's Paradox: A Cautionary Tale in Advanced Analytics Archived 2020-05-10 at the Wayback Machine", Significance.
- ^ Marios G. Pavlides & Michael D. Perlman (August 2009). "How Likely is Simpson's Paradox?". The American Statistician. 63 (3): 226–233. doi:10.1198/tast.2009.09007. S2CID 17481510.
- ^ Kock, N. (2015). How likely is Simpson's paradox in path models? International Journal of e-Collaboration, 11(1), 1–7.
- ^ Norton, H. James; Divine, George (August 2015). "Simpson's paradox ... and how to avoid it". Significance. 12 (4): 40–43. doi:10.1111/j.1740-9713.2015.00844.x.
- ^ Pearl, Judea (2014). "Understanding Simpson's Paradox". The American Statistician. 68 (1): 8–13. doi:10.2139/ssrn.2343788. S2CID 2626833.
- ^ Pearl, Judea (1993). "Graphical Models, Causality, and Intervention". Statistical Science. 8 (3): 266–269. doi:10.1214/ss/1177010894.
- ^ a b Pearl, J.; Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. New York, NY: Basic Books.
- ^ Shpitser, I.; Pearl, J. (2006). Dechter, R.; Richardson, T.S. (eds.). "Identification of Conditional Interventional Distributions". Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence. Corvallis, OR: AUAI Press: 437–444.
- ^ Blyth, Colin R. (June 1972). "On Simpson's Paradox and the Sure-Thing Principle". Journal of the American Statistical Association. 67 (338): 364–366. doi:10.1080/01621459.1972.10482387. ISSN 0162-1459.
- ^ Greenland, Sander (2021-11-01). "Noncollapsibility, confounding, and sparse-data bias. Part 2: What should researchers make of persistent controversies about the odds ratio?". Journal of Clinical Epidemiology. 139: 264–268. doi:10.1016/j.jclinepi.2021.06.004. ISSN 0895-4356. PMID 34119647.
- ^ Hernán, Miguel A.; Clayton, David; Keiding, Niels (June 2011). "The Simpson's paradox unraveled". International Journal of Epidemiology. 40 (3): 780–785. doi:10.1093/ije/dyr041. ISSN 1464-3685. PMC 3147074. PMID 21454324.
Bibliography edit
- Leila Schneps and Coralie Colmez, Math on trial. How numbers get used and abused in the courtroom, Basic Books, 2013. ISBN 978-0-465-03292-1. (Sixth chapter: "Math error number 6: Simpson's paradox. The Berkeley sex bias case: discrimination detection").
External links edit
- Simpson's Paradox at the Stanford Encyclopedia of Philosophy, by Jan Sprenger and Naftali Weinberger.
- How statistics can be misleading – Mark Liddell – TED-Ed video and lesson.
- Pearl, Judea, "Understanding Simpson's Paradox" (PDF)
- Simpson's Paradox, a short article by Alexander Bogomolny on the vector interpretation of Simpson's paradox
- The Wall Street Journal column "The Numbers Guy" for December 2, 2009 dealt with recent instances of Simpson's paradox in the news. Notably a Simpson's paradox in the comparison of unemployment rates of the 2009 recession with the 1983 recession.
- At the Plate, a Statistical Puzzler: Understanding Simpson's Paradox by Arthur Smith, August 20, 2010
- Simpson's Paradox, a video by Henry Reich of MinutePhysics