sRGB is a standard RGB (red, green, blue) color space that HP and Microsoft created cooperatively in 1996 to use on monitors, printers, and the World Wide Web.[2] It was subsequently standardized by the International Electrotechnical Commission (IEC) as IEC 61966-2-1:1999.[1] sRGB is the current defined standard colorspace for the web, and it is usually the assumed colorspace for images that are neither tagged for a colorspace nor have an embedded color profile.
| IEC 61966-2-1 Default RGB Colour Space - sRGB | |
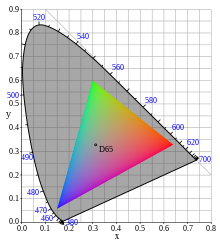 sRGB colors situated at calculated position in CIE 1931 chromaticity diagram. Luminance set so that to avoid mach bands. | |
| Abbreviation | sRGB |
|---|---|
| Status | Published |
| Year started | 1996 |
| First published | October 18, 1999[1] |
| Organization | IEC[1] |
| Committee | TC/SC: TC 100/TA 2[1] |
| Base standards | IEC 61966 Colour Measurement and Management in Multimedia Systems and Equipment |
| Domain | Color space, color model |
| Website | webstore |
sRGB essentially codifies the display specifications for the computer monitors in use at that time, which greatly aided its acceptance. sRGB uses the same color primaries and white point as ITU-R BT.709 standard for HDTV,[3] a transfer function (or gamma) compatible with the era's CRT displays, and a viewing environment designed to match typical home and office viewing conditions.
sRGB definition edit
Gamut edit
| Chromaticity | Red | Green | Blue | White point |
|---|---|---|---|---|
| x | 0.6400 | 0.3000 | 0.1500 | 0.3127 |
| y | 0.3300 | 0.6000 | 0.0600 | 0.3290 |
| Y | 0.2126 | 0.7152 | 0.0722 | 1.0000 |
sRGB defines the chromaticities of the red, green, and blue primaries, the colors where one of the three channels is nonzero and the other two are zero. The gamut of chromaticities that can be represented in sRGB is the color triangle defined by these primaries, which are set such that the range of colors inside the triangle is well within the range of colors visible to a human with normal trichromatic vision. As with any RGB color space, for non-negative values of R, G, and B it is not possible to represent colors outside this triangle.
The primaries come from HDTV (ITU-R BT.709), which are somewhat different from those for older color TV systems (ITU-R BT.601). These values were chosen to reflect the approximate color of consumer CRT phosphors at the time of its design. Since flat-panel displays at the time were generally designed to emulate CRT characteristics, the values also reflected prevailing practice for other display devices as well.[1]
Transfer function ("gamma") edit
The IEC specification indicates a reference display with a nominal gamma of 2.2, which the sRGB working group determined was representative of the CRTs used with Windows operating systems at the time.[2] The ability to directly display sRGB images on a CRT without any lookup greatly helped sRGB's adoption[citation needed]. Gamma also usefully encodes more data near the black, which reduces visible noise and quantization artifacts.
The standard further defines a opto-electronic transfer function (OETF), which defines the conversion of linear light or signal intensity to a gamma-compressed image data. This curve is approximately the inverse of the display's , but with some adjustments to avoid an infinite slope at zero.[4] Near zero, a power curve intercepts a straight-line section that leads to zero. This prevents the infinite slope at zero that would occur if a plain power curve was used.
In practice a pure may be used with sRGB data with very little difference. This improves computational performance and is referred to as "simple sRGB" by Adobe, This is also how most displays transform the encoded image data to the screen.
Computing the transfer function edit
A straight line that passes through (0,0) is , and a gamma curve that passes through (1,1) is
If these are joined at the point (X,X/Φ) then:
To avoid a kink where the two segments meet, the derivatives must be equal at this point:
We now have two equations. If we take the two unknowns to be X and Φ then we can solve to give
The values A = 0.055 and Γ = 2.4 were chosen[how?] so the curve closely resembled the gamma-2.2 curve. This gives X ≈ 0.0392857, Φ ≈ 12.9232102. These values, rounded to X = 0.03928, Φ = 12.92321 sometimes describe sRGB conversion.[5]
Draft publications by sRGB's creators further rounded Φ = 12.92,[2] resulting in a small discontinuity in the curve. Some authors adopted these incorrect values, in part because the draft paper was freely available and the official IEC standard is behind a paywall.[6] For the standard, the rounded value of Φ was kept and X was recomputed as 0.04045 to make the curve continuous, resulting in a slope discontinuity from 1/12.92 below the intersection to 1/12.70 above.
Viewing environment edit
| Parameter | Value |
|---|---|
| Screen luminance level | 80 cd/m2 |
| Illuminant white point | x = 0.3127, y = 0.3290 (D65) |
| Image surround reflectance | 20% (~medium gray) |
| Encoding ambient illuminance level | 64 lux |
| Encoding ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Encoding viewing flare | 1.0% |
| Typical ambient illuminance level | 200 lux |
| Typical ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Typical viewing flare | 5.0% |
The sRGB specification assumes a dimly lit encoding (creation) environment with an ambient correlated color temperature (CCT) of 5003 K. This differs from the CCT of the illuminant (D65). Using D50 for both would have made the white point of most photographic paper appear excessively blue.[7][8] The other parameters, such as the luminance level, are representative of a typical CRT monitor.
For optimal results, the ICC recommends using the encoding viewing environment (i.e., dim, diffuse lighting) rather than the less-stringent typical viewing environment.[2]
Transformation edit
From sRGB to CIE XYZ edit
The sRGB component values , , are in the range 0 to 1. When represented digitally as 8-bit numbers, these color component values are in the range of 0 to 255, and should be divided (in a floating point representation) by 255 to convert to the range of 0 to 1.
where is , , or .
These gamma-expanded values (sometimes called "linear values" or "linear-light values") are multiplied by a matrix to obtain CIE XYZ (the matrix has infinite precision, any change in its values or adding non-zeroes is not allowed):
This is actually the matrix for BT.709 primaries, not just for sRGB, the second row corresponds to the BT.709-2 luma coefficients (BT.709-1 had a typo in these coefficients).
From CIE XYZ to sRGB edit
The CIE XYZ values must be scaled so that the Y of D65 ("white") is 1.0 (X = 0.9505, Y = 1.0000, Z = 1.0890). This is usually true but some color spaces use 100 or other values (such as in CIELAB, when using specified white points).
The first step in the calculation of sRGB from CIE XYZ is a linear transformation, which may be carried out by a matrix multiplication. (The numerical values below match those in the official sRGB specification,[1][9] which corrected small rounding errors in the original publication[2] by sRGB's creators, and assume the 2° standard colorimetric observer for CIE XYZ.[2]) This matrix depends on the bitdepth.
These linear RGB values are not the final result; gamma correction must still be applied. The following formula transforms the linear values into sRGB:
where is , , or .
These gamma-compressed values (sometimes called "non-linear values") are usually clipped to the 0 to 1 range. This clipping can be done before or after the gamma calculation, or done as part of converting to 8 bits. If values in the range 0 to 255 are required, e.g. for video display or 8-bit graphics, the usual technique is to multiply by 255 and round to an integer.
Usage edit
Due to the standardization of sRGB on the Internet, on computers, and on printers, many low- to medium-end consumer digital cameras and scanners use sRGB as the default (or only available) working color space. However, consumer-level CCDs are typically uncalibrated, meaning that even though the image is being labeled as sRGB, one can not conclude that the image is color-accurate sRGB.
If the color space of an image is unknown and it is an 8 bit image format, sRGB is usually the assumed default, in part because color spaces with a larger gamut need a higher bit depth to maintain a low color error rate (∆E). An ICC profile or a lookup table may be used to convert sRGB to other color spaces. ICC profiles for sRGB are widely distributed, and the ICC distributes several variants of sRGB profiles,[10] including variants for ICCmax, version 4, and version 2. Version 4 is generally recommended, but version 2 is still commonly used and is the most compatible with other software including browsers. Version 2 of the ICC profile specification does not officially support piecewise parametric curve encoding ("para"), though version 2 does support simple power-law functions.[10] Nevertheless, lookup tables are more commonly used as they are computationally more efficient.[citation needed] Even when parametric curves are used, software will often reduce to a run-time lookup table for efficient processing.[citation needed]
As the sRGB gamut meets or exceeds the gamut of a low-end inkjet printer, an sRGB image is often regarded as satisfactory for home printing. sRGB is sometimes avoided by high-end print publishing professionals because its color gamut is not big enough, especially in the blue-green colors, to include all the colors that can be reproduced in CMYK printing. Images intended for professional printing via a fully color-managed workflow (e.g. prepress output) sometimes use another color space such as Adobe RGB (1998), which accommodates a wider gamut. Such images used on the Internet may be converted to sRGB using color management tools that are usually included with software that works in these other color spaces.
The two dominant programming interfaces for 3D graphics, OpenGL and Direct3D, have both incorporated support for the sRGB gamma curve.
OpenGL supports textures with sRGB gamma encoded color components (first introduced with EXT_texture_sRGB extension,[11] added to the core in OpenGL 2.1) and rendering into sRGB gamma encoded framebuffers (first introduced with EXT_framebuffer_sRGB extension,[12] added to the core in OpenGL 3.0). Correct mipmapping and interpolation of sRGB gamma textures has direct hardware support in texturing units of most modern GPUs (for example nVidia GeForce 8 performs conversion from 8-bit texture to linear values before interpolating those values), and does not have any performance penalty.[13]
sYCC edit
Amendment 1 to IEC 61966-2-1:1999, approved in 2003, includes the definition of a Y′Cb′Cr′ color representation called sYCC. Although the RGB color primaries are based on BT.709, the equations for transformation from sRGB to sYCC and vice versa are based on BT.601. sYCC uses 8 bits for the components resulting in a range of approximately 0–1 for Y; -0.5–0.5 for C.[14] The amendment also contains a 10-bit-or-more encoding called bg-sRGB where 0–1 is mapped to -384⁄510...639⁄510, and bg-sYCC using the same number of bits for a range of approximately -0.75–1.25 for Y; -1–1 for C.[14]
As this conversion can result in sRGB values outside the range 0–1, the amendment describes how to apply the gamma correction to negative values, by applying −f(−x) when x is negative (and f is the sRGB↔linear functions described above). This is also used by scRGB.
The amendment also recommends a higher-precision XYZ to sRGB matrix using seven decimal points, to more accurately invert the sRGB to XYZ matrix (which remains at the precision shown above):
- .[14]
References edit
- ^ a b c d e f "IEC 61966-2-1:1999". IEC Webstore. International Electrotechnical Commission. Retrieved 3 March 2017.
- ^ a b c d e f Michael Stokes; Matthew Anderson; Srinivasan Chandrasekar; Ricardo Motta (November 5, 1996). "A Standard Default Color Space for the Internet – sRGB, Version 1.10". Archived from the original on Jul 3, 2023.
- ^ Charles A. Poynton (2003). Digital Video and HDTV: Algorithms and Interfaces. Morgan Kaufmann. ISBN 1-55860-792-7.
- ^ "The Importance of Terminology and sRGB Uncertainty". Colour Science. 2015-12-05. Retrieved 2021-11-05.
- ^ Phil Green & Lindsay W. MacDonald (2002). Colour Engineering: Achieving Device Independent Colour. John Wiley and Sons. ISBN 0-471-48688-4.
- ^ Jon Y. Hardeberg (2001). Acquisition and Reproduction of Color Images: Colorimetric and Multispectral Approaches. Universal-Publishers.com. ISBN 1-58112-135-0.
- ^ Rodney, Andrew (2005). Color Management for Photographers. Focal Press. p. 121. ISBN 978-0-240-80649-5.
- ^ "Why Calibrate Monitor to D65 When Light Booth is D50". X-Rite. Retrieved 2022-09-11.
- ^ "How to interpret the sRGB color space" (PDF). color.org. Retrieved 17 October 2017.
- ^ a b sRGB profiles, ICC
- ^ "EXT_texture_sRGB". 24 January 2007. Retrieved 12 May 2020.
- ^ "EXT_framebuffer_sRGB". 17 September 2010. Retrieved 12 May 2020.
- ^ "GPU Gems 3: Chapter 24. The Importance of Being Linear, section 24.4.1". NVIDIA Corporation. Retrieved 3 March 2017.
- ^ a b c "IEC 61966-2-1:1999 Multimedia systems and equipment – Colour measurement and management – Part 2-1: Colour management – Default RGB colour space – sRGB: Amendment 1". International Electrotechnical Commission. 2003.
Standards edit
- IEC 61966-2-1:1999 is the official specification of sRGB. It provides viewing environment, encoding, and colorimetric details.
- Amendment A1:2003 to IEC 61966-2-1:1999 describes an sYCC encoding for YCbCr color spaces, an extended-gamut RGB encoding, and a CIELAB transformation.
- sRGB, International Color Consortium
- The fourth working draft of IEC 61966-2-1 is available online, but is not the complete standard. It can be downloaded from www2.units.it.
- Archive copy of sRGB.com, now unavailable, containing much information on the design, principles, and use of sRGB
External links edit
- International Color Consortium
- Conversion matrices for RGB vs. XYZ conversion
- Test that shows whether your display is 2.2 gamma or sRGB
- Will the Real sRGB Profile Please Stand Up?, analyzes the inconsistency among sRGB ICC profiles
- Color spaces - REC.709 vs. sRGB from image-engineering.de, with a graph comparing two transfer functions

