This extensive use of "we"'s tone or style may not reflect the encyclopedic tone used on Wikipedia. (July 2021) |
The Richardson–Lucy algorithm, also known as Lucy–Richardson deconvolution, is an iterative procedure for recovering an underlying image that has been blurred by a known point spread function. It was named after William Richardson and Leon B. Lucy, who described it independently.[1][2]
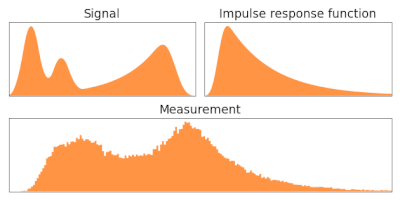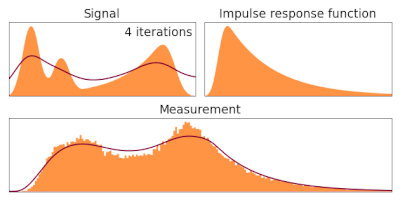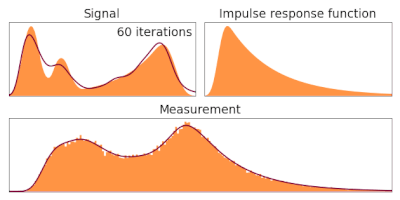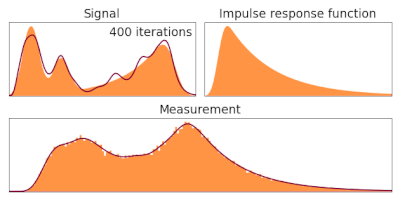
Description edit
When an image is produced using an optical system and detected using photographic film or a charge-coupled device, for instance, it is inevitably blurred, with an ideal point source not appearing as a point but being spread out into what is known as the point spread function. Extended sources can be decomposed into the sum of many individual point sources, thus the observed image can be represented in terms of a transition matrix p operating on an underlying image:
where is the intensity of the underlying image at pixel and is the detected intensity at pixel . In general, a matrix whose elements are describes the portion of light from source pixel j that is detected in pixel i. In most good optical systems (or in general, linear systems that are described as shift invariant) the transfer function p can be expressed simply in terms of the spatial offset between the source pixel j and the observation pixel i:
where is called a point spread function. In that case the above equation becomes a convolution. This has been written for one spatial dimension, but of course most imaging systems are two dimensional, with the source, detected image, and point spread function all having two indices. So a two dimensional detected image is a convolution of the underlying image with a two dimensional point spread function plus added detection noise.
In order to estimate given the observed and a known , the following iterative procedure is employed in which the estimate of (called ) for iteration number t is updated as follows:
where
and is assumed. It has been shown empirically that if this iteration converges, it converges to the maximum likelihood solution for .[3]
Writing this more generally for two (or more) dimensions in terms of convolution with a point spread function P:
where the division and multiplication are element wise, indicates a 2D convolution, and is the flipped point spread function.
In problems where the point spread function is not known a priori, a modification of the Richardson–Lucy algorithm has been proposed, in order to accomplish blind deconvolution.[4]
Derivation edit
In the context of fluorescence microscopy, the probability of measuring a set of number of photons (or digitalization counts proportional to detected light) for expected values for a detector with pixels is given by
it is convenient to work with since in the context of maximum likelihood estimation the aim is to locate the maximum of the likelihood function without concern for its absolute value.
Again since is a constant, it will not give any additional information regarding the position of the maximum, so let's consider
where is something that shares the same maximum position as . Now let's consider that comes from a ground truth and a measurement which we assume to be linear. Then
where a matrix multiplication is implied. We can also write this in the form
where we can see how , mixes or blurs the ground truth.
It can also be shown that the derivative of an element of , with respect to some other element of can be written as:
-
(1)
-
Tip: it's easy to see this by writing a matrix of say (5 x 5) and two arrays and of 5 elements and check it. This last equation can interpreted as how much one element of , say element influences the other elements (and of course the case is also taken into account). For example in a typical case an element of the ground truth will influence nearby elements in but not the very distant ones (a value of is expected on those matrix elements).
Now, the key and arbitrary step: is not known but we want to estimate it with , let's call and the estimated ground truths while we are using the RL algorithm, where the hat symbol is used to distinguish ground truth from estimator of the ground truth
-
(2)
-
Where stands for a -dimensional gradient. If we work on the derivative of we get
and if we now use (1) we get
But we can also note that by definition of transpose matrix. And hence
-
(3)
-
Then if we consider spanning all the elements from to this equation can be rewritten in its vectorial form
where is a matrix and , and are vectors. Let's now propose the following arbitrary and key step
-
(4)
-
where is a vector of ones of size (same as , and ) and the division is element-wise. Using (3) and (4) we can rewrite (2) as
which yields
-
(5)
-
Where division refers to element-wise matrix division and operates as a matrix but the division and the product (implicit after ) are element-wise. Also, can be calculated because we assume
- The initial guess is known (and is typically set to be the experimental data)
- The measurement function is known
On the other hand is the experimental data. Therefore, equation (5) applied successively, provides an algorithm to estimate our ground truth by ascending (since it moves in the direction of the gradient of the likelihood) in the likelihood landscape. It has not been demonstrated in this derivation that it converges and no dependence on the initial choice is shown. Note that equation (2) provides a way of following the direction that increases the likelihood but the choice of the log-derivative is arbitrary. On the other hand equation (4) introduces a way of weighting the movement from the previous step in the iteration. Note that if this term was not present in (5) then the algorithm would output a movement in the estimation even if . It's worth noting that the only strategy used here is to maximize the likelihood at all cost, so artifacts on the image can be introduced. It is worth noting that no prior knowledge on the shape of the ground truth is used in this derivation.
Software edit
- RawTherapee (since v.2.3)
See also edit
References edit
- ^ Richardson, William Hadley (1972). "Bayesian-Based Iterative Method of Image Restoration". Journal of the Optical Society of America. 62 (1): 55–59. Bibcode:1972JOSA...62...55R. doi:10.1364/JOSA.62.000055.
- ^ Lucy, L. B. (1974). "An iterative technique for the rectification of observed distributions". Astronomical Journal. 79 (6): 745–754. Bibcode:1974AJ.....79..745L. doi:10.1086/111605.
- ^ Shepp, L. A.; Vardi, Y. (1982), "Maximum Likelihood Reconstruction for Emission Tomography", IEEE Transactions on Medical Imaging, 1 (2): 113–22, doi:10.1109/TMI.1982.4307558, PMID 18238264
- ^ Fish D. A.; Brinicombe A. M.; Pike E. R.; Walker J. G. (1995), "Blind deconvolution by means of the Richardson–Lucy algorithm" (PDF), Journal of the Optical Society of America A, 12 (1): 58–65, Bibcode:1995JOSAA..12...58F, doi:10.1364/JOSAA.12.000058, S2CID 42733042, archived from the original (PDF) on 2019-01-10