Richardson–Lucy deconvolution

Not to be confused with Modified Richardson iteration.

The Richardson–Lucy algorithm, also known as Lucy–Richardson deconvolution, is an iterative procedure for recovering an underlying image that has been blurred by a known point spread function. It was named after William Richardson and Leon B. Lucy, who described it independently.

The use of Richardson–Lucy deconvolution to recover a signal blurred by an impulse response function.

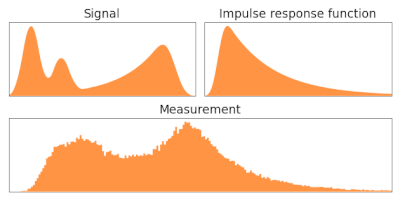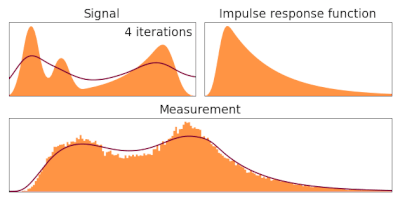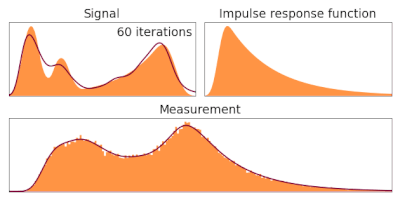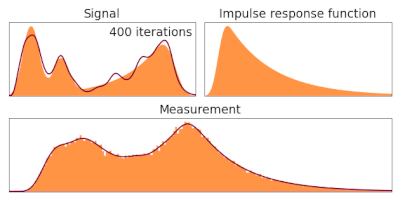
Description

When an image is produced using an optical system and detected using photographic film or a charge-coupled device, for example, it is inevitably blurred, with an ideal point source not appearing as a point but being spread out into what is known as the point spread function. Extended sources can be decomposed into the sum of many individual point sources, thus the observed image can be represented in terms of a transition matrix p operating on an underlying image:

$d_{i}=\sum _{j}p_{i,j}u_{j}\,$

where $u_{j}$ is the intensity of the underlying image at pixel $j$ and $d_{i}$ is the detected intensity at pixel $i$. In general, a matrix whose elements are $p_{i,j}$ describes the portion of light from source pixel j that is detected in pixel i. In most good optical systems (or in general, linear systems that are described as shift invariant) the transfer function p can be expressed simply in terms of the spatial offset between the source pixel j and the observation pixel i:

$p_{i,j}=P(i-j)$

where $P(\Delta i)$ is called a point spread function. In that case the above equation becomes a convolution. This has been written for one spatial dimension, but most imaging systems are two dimensional, with the source, detected image, and point spread function all having two indices. So a two dimensional detected image is a convolution of the underlying image with a two dimensional point spread function $P(\Delta x,\Delta y)$ plus added detection noise.

In order to estimate $u_{j}$ given the observed $d_{i}$ and a known $P(\Delta i_{x},\Delta j_{y})$, the following iterative procedure is employed in which the estimate of $u_{j}$ (called ${\hat {u}}_{j}^{(t)}$) for iteration number t is updated as follows:

${\hat {u}}_{j}^{(t+1)}={\hat {u}}_{j}^{(t)}\sum _{i}{\frac {d_{i}}{c_{i}}}p_{ij}$

where

$c_{i}=\sum _{j}p_{ij}{\hat {u}}_{j}^{(t)}$

and $\sum _{j}p_{ij}=1$ is assumed. It has been shown empirically that if this iteration converges, it converges to the maximum likelihood solution for $u_{j}$.

Writing this more generally for two (or more) dimensions in terms of convolution with a point spread function P:

${\hat {u}}^{(t+1)}={\hat {u}}^{(t)}\cdot \left({\frac {d}{{\hat {u}}^{(t)}\otimes P}}\otimes P^{*}\right)$

where the division and multiplication are element wise, $\otimes$ indicates a 2D convolution, and $P^{*}$ is the flipped point spread function.

In problems where the point spread function $p_{ij}$ is not known a priori, a modification of the Richardson–Lucy algorithm has been proposed, in order to accomplish blind deconvolution.

Software

• RawTherapee (since v.2.3)

See also

• Deconvolution
• Wiener filter (deconvolution in the presence of additive noise)