The article's lead section may need to be rewritten. The reason given is: The lead could do with an additional sentence or two of non-expert introduction before talking about equations and detail that requires a greater-than-high-school understanding of maths and physics. (February 2024) |
A photon sphere[1] or photon circle[2] is an area or region of space where gravity is so strong that photons are forced to travel in orbits, which is also sometimes called the last photon orbit.[3] The radius of the photon sphere, which is also the lower bound for any stable orbit, is, for a Schwarzschild black hole,
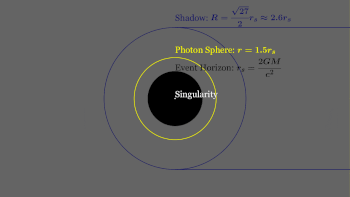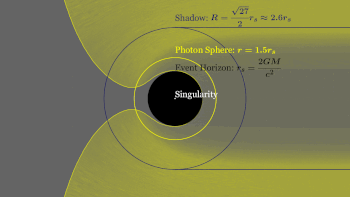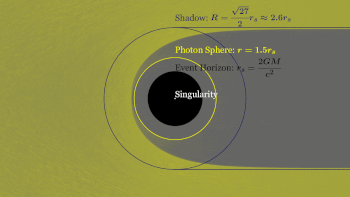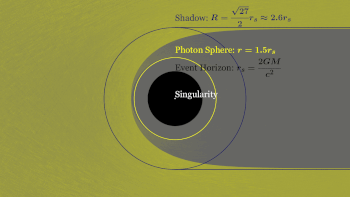
where G is the gravitational constant, M is the mass of the black hole, c is the speed of light in vacuum, and rs is the Schwarzschild radius (the radius of the event horizon); see below for a derivation of this result.
This equation entails that photon spheres can only exist in the space surrounding an extremely compact object (a black hole or possibly an "ultracompact" neutron star[4]).
The photon sphere is located farther from the center of a black hole than the event horizon. Within a photon sphere, it is possible to imagine a photon that is emitted (or reflected) from the back of one's head and, following an orbit of the black hole, is then intercepted by the person's eye, allowing one to see the back of the head. For non-rotating black holes, the photon sphere is a sphere of radius 3/2 rs. There are no stable free-fall orbits that exist within or cross the photon sphere. Any free-fall orbit that crosses it from the outside spirals into the black hole. Any orbit that crosses it from the inside escapes to infinity or falls back in and spirals into the black hole. No unaccelerated orbit with a semi-major axis less than this distance is possible, but within the photon sphere, a constant acceleration will allow a spacecraft or probe to hover above the event horizon.
Another property of the photon sphere is centrifugal force (note: not centripetal) reversal.[5] Outside the photon sphere, the faster one orbits, the greater the outward force one feels. Centrifugal force falls to zero at the photon sphere, including non-freefall orbits at any speed, i.e. an object weighs the same no matter how fast it orbits, and becomes negative inside it. Inside the photon sphere, faster orbiting leads to greater weight or inward force. This has serious ramifications for the fluid dynamics of inward fluid flow.
A rotating black hole has two photon spheres. As a black hole rotates, it drags space with it. The photon sphere that is closer to the black hole is moving in the same direction as the rotation, whereas the photon sphere further away is moving against it. The greater the angular velocity of the rotation of a black hole, the greater the distance between the two photon spheres. Since the black hole has an axis of rotation, this only holds true if approaching the black hole in the direction of the equator. In a polar orbit, there is only one photon sphere. This is because when approaching at this angle, the possibility of traveling with or against the rotation does not exist. The rotation will instead cause the orbit to precess.[6]
Derivation for a Schwarzschild black hole edit
Since a Schwarzschild black hole has spherical symmetry, all possible axes for a circular photon orbit are equivalent, and all circular orbits have the same radius.
This derivation involves using the Schwarzschild metric, given by
For a photon traveling at a constant radius r (i.e. in the φ-coordinate direction), . Since it is a photon, (a "light-like interval"). We can always rotate the coordinate system such that is constant, (e.g., ).
Setting ds, dr and dθ to zero, we have
Re-arranging gives
To proceed, we need the relation . To find it, we use the radial geodesic equation
Non vanishing -connection coefficients are
where .
We treat photon radial geodesics with constant r and , therefore
Substituting it all into the radial geodesic equation (the geodesic equation with the radial coordinate as the dependent variable), we obtain
Comparing it with what was obtained previously, we have
where we have inserted radians (imagine that the central mass, about which the photon is orbiting, is located at the centre of the coordinate axes. Then, as the photon is travelling along the -coordinate line, for the mass to be located directly in the centre of the photon's orbit, we must have radians).
Hence, rearranging this final expression gives
which is the result we set out to prove.
Photon orbits around a Kerr black hole edit
In contrast to a Schwarzschild black hole, a Kerr (spinning) black hole does not have spherical symmetry, but only an axis of symmetry, which has profound consequences for the photon orbits, see e.g. Cramer[2] for details and simulations of photon orbits and photon circles. There are two circular photon orbits in the equatorial plane (prograde and retrograde), with different Boyer–Lindquist radii:
where is the angular momentum per unit mass of the black hole.[7] There exist other constant-radius orbits, but they have more complicated paths which oscillate in latitude about the equator.[7]
References edit
- ^ Bennett, Jay (April 10, 2019). "Astronomers Capture First-Ever Image of a Supermassive Black Hole". Smithsonian.com. Smithsonian Institution. Archived from the original on April 13, 2021. Retrieved April 15, 2019.
- ^ a b Cramer, Claes R. (1997). "Using the Uncharged Kerr Black Hole as a Gravitational Mirror". General Relativity and Gravitation. 29 (4): 445–454. arXiv:gr-qc/9510053. Bibcode:1997GReGr..29..445C. doi:10.1023/A:1018878515046. S2CID 9517046.
- ^ "What the Sight of a Black Hole Means to a Black Hole Physicist" Archived 2021-05-14 at the Wayback Machine, Quanta Magazine, 10 April 2019: "a region defined by the location closest to the black hole where a beam of light could orbit on a circle, known as the “last photon orbit”."
- ^ Properties of ultracompact neutron stars Archived 2021-05-06 at the Wayback Machine.
- ^ Abramowicz, Marek (1990). "Centrifugal-force reversal near a Schwarzschild black hole". Monthly Notices of the Royal Astronomical Society. 245: 720. Bibcode:1990MNRAS.245..720A.
- ^ Hirata, Christopher M. (December 2011). "Lecture XXVII: Kerr black holes: II. Precession, circular orbits, and stability" (PDF). Caltech. Retrieved 5 March 2018.
- ^ a b Teo, Edward (2003). "Spherical Photon Orbits Around a Kerr Black Hole" (PDF). General Relativity and Gravitation. 35 (11): 1909–1926. Bibcode:2003GReGr..35.1909T. doi:10.1023/A:1026286607562. ISSN 0001-7701. S2CID 117097507. Archived (PDF) from the original on 2020-06-03. Retrieved 2010-08-24.
