Linear polarization

Diagram of the electric field of a light wave (blue), linear-polarized along a plane (purple line), and consisting of two orthogonal, in-phase components (red and green waves)

In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation. See polarization for more information.

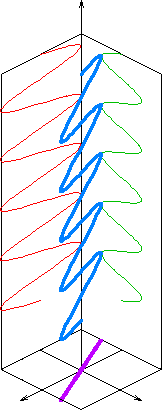
The orientation of a linearly polarized electromagnetic wave is defined by the direction of the electric field vector. For example, if the electric field vector is vertical (alternately up and down as the wave travels) the radiation is said to be vertically polarized.

Mathematical description of linear polarization

The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is (cgs units)

$\mathbf{E} ( \mathbf{r} , t ) = \mid \mathbf{E} \mid \mathrm{Re} \left \{ |\psi\rangle \exp \left [ i \left ( kz-\omega t \right ) \right ] \right \}$

$\mathbf{B} ( \mathbf{r} , t ) = \hat { \mathbf{z} } \times \mathbf{E} ( \mathbf{r} , t )/c$

for the magnetic field, where k is the wavenumber,

$\omega_{ }^{ } = c k$

is the angular frequency of the wave, and $c$ is the speed of light.

Here

$\mid \mathbf{E} \mid$

is the amplitude of the field and

$|\psi\rangle \ \stackrel{\mathrm{def}}{=}\ \begin{pmatrix} \psi_x \\ \psi_y \end{pmatrix} = \begin{pmatrix} \cos\theta \exp \left ( i \alpha_x \right ) \\ \sin\theta \exp \left ( i \alpha_y \right ) \end{pmatrix}$

is the Jones vector in the x-y plane.

The wave is linearly polarized when the phase angles $\alpha_x^{ } , \alpha_y$ are equal,

$\alpha_x = \alpha_y \ \stackrel{\mathrm{def}}{=}\ \alpha$.

This represents a wave polarized at an angle $\theta$ with respect to the x axis. In that case the Jones vector can be written

$|\psi\rangle = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \exp \left ( i \alpha \right )$.

The state vectors for linear polarization in x or y are special cases of this state vector.

If unit vectors are defined such that

$|x\rangle \ \stackrel{\mathrm{def}}{=}\ \begin{pmatrix} 1 \\ 0 \end{pmatrix}$

and

$|y\rangle \ \stackrel{\mathrm{def}}{=}\ \begin{pmatrix} 0 \\ 1 \end{pmatrix}$

then the polarization state can written in the "x-y basis" as

$|\psi\rangle = \cos\theta \exp \left ( i \alpha \right ) |x\rangle + \sin\theta \exp \left ( i \alpha \right ) |y\rangle = \psi_x |x\rangle + \psi_y |y\rangle$.

References

• Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. 

External links

• Animation of Linear Polarization (on YouTube)
• Comparison of Linear Polarization with Circular and Elliptical Polarizations (YouTube Animation)

See also

• Sinusoidal plane-wave solutions of the electromagnetic wave equation
• Polarization
  • Circular polarization
  • Elliptical polarization
• Photon polarization

 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".