In coordination chemistry, the ligand cone angle (θ) is a measure of the steric bulk of a ligand in a transition metal coordination complex. It is defined as the solid angle formed with the metal at the vertex of a cone and the outermost edge of the van der Waals spheres of the ligand atoms at the perimeter of the base of the cone. Tertiary phosphine ligands are commonly classified using this parameter, but the method can be applied to any ligand. The term cone angle was first introduced by Chadwick A. Tolman, a research chemist at DuPont. Tolman originally developed the method for phosphine ligands in nickel complexes, determining them from measurements of accurate physical models.[1][2][3]
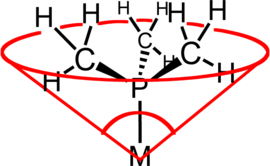
Asymmetric cases
editThe concept of cone angle is most easily visualized with symmetrical ligands, e.g. PR3. But the approach has been refined to include less symmetrical ligands of the type PRR′R″ as well as diphosphines. In such asymmetric cases, the substituent angles' half angles, θi/2, are averaged and then doubled to find the total cone angle, θ. In the case of diphosphines, the θi/2 of the backbone is approximated as half the chelate bite angle, assuming a bite angle of 74°, 85°, and 90° for diphosphines with methylene, ethylene, and propylene backbones, respectively. The Manz cone angle is often easier to compute than the Tolman cone angle:[4][clarification needed]
| Ligand | Angle (°) |
|---|---|
| PH3 | 87[1] |
| PF3 | 104[1] |
| P(OCH3)3 | 107[1] |
| dmpe | 107 |
| depe | 115 |
| P(CH3)3 | 118[1] |
| dppm | 121 |
| dppe | 125 |
| dppp | 127 |
| P(CH2CH3)3 | 132[1] |
| dcpe | 142 |
| P(C6H5)3 | 145[1] |
| P(cyclo-C6H11)3 | 179[1] |
| P(t-Bu)3 | 182[1] |
| P(C6F5)3 | 184[1] |
| P(C6H4-2-CH3)3 | 194[1] |
| P(2,4,6-Me3C6H2)3 | 212 |
Variations
editThe Tolman cone angle method assumes empirical bond data and defines the perimeter as the maximum possible circumscription of an idealized free-spinning substituent. The metal-ligand bond length in the Tolman model was determined empirically from crystal structures of tetrahedral nickel complexes. In contrast, the solid-angle concept derives both bond length and the perimeter from empirical solid state crystal structures.[5][6] There are advantages to each system.
If the geometry of a ligand is known, either through crystallography or computations, an exact cone angle (θ) can be calculated.[7][8][9] No assumptions about the geometry are made, unlike the Tolman method.
Application
editThe concept of cone angle is of practical importance in homogeneous catalysis because the size of the ligand affects the reactivity of the attached metal center. In an example,[10] the selectivity of hydroformylation catalysts is strongly influenced by the size of the coligands. Despite being monovalent, some phosphines are large enough to occupy more than half of the coordination sphere of a metal center. Recent research has found that other descriptors—such as percent buried volume—are more accurate than cone angle at capturing the relevant steric effects of the phosphine ligand(s) when bound to the metal center.[11]
See also
edit- Steric effects (versus electronic effects)
- Tolman electronic parameter
References
edit- ^ a b c d e f g h i j k Tolman, Chadwick A. (1970-05-01). "Phosphorus ligand exchange equilibriums on zerovalent nickel. Dominant role for steric effects". J. Am. Chem. Soc. 92 (10): 2956–2965. doi:10.1021/ja00713a007.
- ^ Tolman, C. A.; Seidel, W. C.; Gosser, L. W. (1974-01-01). "Formation of three-coordinate nickel(0) complexes by phosphorus ligand dissociation from NiL4". J. Am. Chem. Soc. 96 (1): 53–60. doi:10.1021/ja00808a009.
- ^ Tolman, C. A. (1977). "Steric Effects of Phosphorus Ligands in Organometallic Chemistry and Homogeneous Catalysis". Chem. Rev. 77 (3): 313–48. doi:10.1021/cr60307a002.
- ^ Manz, T. A.; Phomphrai, K.; Medvedev, G.; Krishnamurthy, B. B.; Sharma, S.; Haq, J.; Novstrup, K. A.; Thomson, K. T.; Delgass, W. N.; Caruthers, J. M.; Abu-Omar, M. M. (2007). "Structure−Activity Correlation in Titanium Single-Site Olefin Polymerization Catalysts Containing Mixed Cyclopentadienyl/Aryloxide Ligation". J. Am. Chem. Soc. 129 (13): 3776–3777. doi:10.1021/ja0640849. PMID 17348648.
- ^ Immirzi, A.; Musco, A. (1977). "A method to measure the size of phosphorus ligands in coordination complexes". Inorg. Chim. Acta. 25: L41–L42. doi:10.1016/S0020-1693(00)95635-4.[dead link]
- ^ Niksch, Tobias; Görls, Helmar; Weigand, Wolfgang (2009). "The Extension of the Solid-Angle Concept to Bidentate Ligands". Eur. J. Inorg. Chem. 2010 (1): 95–105. doi:10.1002/ejic.200900825.
- ^ Bilbrey, Jenna A.; Kazez, Arianna H.; Locklin, J.; Allen, Wesley D. (2013). "Exact ligand cone angles". Journal of Computational Chemistry. 34 (14): 1189–1197. doi:10.1002/jcc.23217. PMID 23408559. S2CID 23864226.
- ^ "AaronTools". aarontools.readthedocs.io. Retrieved 2023-05-30.
- ^ Petitjean, Michel (2015). "Analytical Algorithms for Ligand Cone Angles Calculations. Application to Triphenylphosphine Palladium Complexes". Comptes Rendus Chimie. 18 (6): 678–684. doi:10.1016/j.crci.2015.04.004.
- ^ Evans, D.; Osborn, J. A.; Wilkinson, G. (1968). "Hydroformylation of Alkenes by Use of Rhodium Complex Catalyst". Journal of the Chemical Society. 33 (21): 3133–3142. doi:10.1039/J19680003133.
- ^ Newman-Stonebraker, Samuel H.; Smith, Sleight R.; Borowski, Julia E.; Peters, Ellyn; Gensch, Tobias; Johnson, Heather C.; Sigman, Matthew S.; Doyle, Abigail G. (2021). "Univariate classification of phosphine ligation state and reactivity in cross-coupling catalysis". Science. 374 (6565): 301–308. Bibcode:2021Sci...374..301N. doi:10.1126/science.abj4213. PMID 34648340. S2CID 238991361.