Graph of a function

For the graph-theoretic representation of a function from a set to the same set, see Functional graph.

Graph of the function f(x)= x ⁴ - 4 ^x
(-2 , +2)

In mathematics, the graph of a function f is the collection of all ordered pairs (x, f(x)). In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a line chart, a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is sometimes referred to as curve sketching. If the function input x is an ordered pair (x₁, x₂) of real numbers, the graph is the collection of all ordered triples (x₁, x₂, f(x₁, x₂)), and its graphical representation is a surface (see three dimensional graph).

The graph of a function on real numbers is identical to the graphic representation of the function. For general functions, the graphic representation cannot be applied and the formal definition of the graph of a function suits the need of mathematical statements, e.g., the closed graph theorem in functional analysis.

The concept of the graph of a function is generalized to the graph of a relation. Note that although a function is always identified with its graph, they are not the same because it will happen that two functions with different codomain could have the same graph. For example, the cubic polynomial mentioned below is a surjection if its codomain is the real numbers but it is not if its codomain is the complex field.

To test if a graph of a curve is a function of x, use the vertical line test. To test if a graph of a curve is a function of y, use the horizontal line test. If the function has an inverse, the graph of the inverse can be found by reflecting the graph of the original function over the line $y = x$.

In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see Plot (graphics) for details.

Examples

Graph of the function f(x)=x³ - 9x

Functions of one variable

The graph of the function.

$f(x)= \left\{\begin{matrix} a, & \mbox{if }x=1 \\ d, & \mbox{if }x=2 \\ c, & \mbox{if }x=3. \end{matrix}\right.$

is

{(1,a), (2,d), (3,c)}.

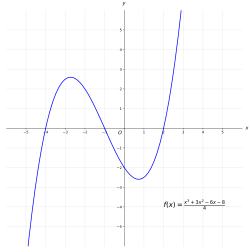
The graph of the cubic polynomial on the real line

$f(x)={{x^3}-9x} \!\$

is

{(x, x³-9x) : x is a real number}.

If this set is plotted on a Cartesian plane, the result is a curve (see figure).

Graph of the function f(x, y) = sin(x²)·cos(y²).

Functions of two variables

The graph of the trigonometric function on the real line

f(x, y) = sin(x²)·cos(y²)

is

{(x, y, sin(x²)·cos(y²)) : x and y are real numbers}.

If this set is plotted on a three dimensional Cartesian coordinate system, the result is a surface (see figure).

Functions of two variables

You can see this set on a two dimensional cartesian coordinate system (X,Y), using color to display the third coordinate Z.

• 

  Z = Sin(x)^2 + Sin(y)^2

Normal to a graph

Given a function f of n variables: $x=x_1, \dotsc ,x_n$, the normal to the graph is

$(\nabla f, -1)$

(up to multiplication by a constant). This is seen by considering the graph as a level set of the function $g(x,z) = f(x) - z$, and using that $\nabla g$ is normal to the level sets.

Generalizations

The graph of a function is contained in a cartesian product of sets. An XY plane is a cartesian product of two lines, called X and Y, while a cylinder is a cartesian product of a line and a circle, whose height, radius, and angle assign precise locations of the points. Fibre bundles aren't cartesian products, but appear to be up close. There is a corresponding notion of a graph on a fibre bundle called a section.

Tools for plotting function graphs

Hardware

• Graphing calculator
• Oscilloscope
• Paper and pencil

Software

See List of graphing software

See also

• Asymptote
• Critical point
• Derivative
• Epigraph
• Chart
• Stationary point
• Slope
• Solution point
• Tetraview
• Vertical translation
• Y-intercept
• Graph Theory

External links

• Interactive function graph plotter

• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.