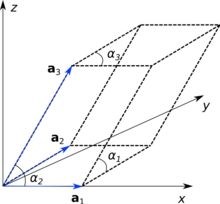
In crystallography, a fractional coordinate system (crystal coordinate system) is a coordinate system in which basis vectors used to the describe the space are the lattice vectors of a crystal (periodic) pattern. The selection of an origin and a basis define a unit cell, a parallelotope (i.e., generalization of a parallelogram (2D) or parallelepiped (3D) in higher dimensions) defined by the lattice basis vectors where is the dimension of the space. These basis vectors are described by lattice parameters (lattice constants) consisting of the lengths of the lattice basis vectors and the angles between them .
Most cases in crystallography involve two- or three-dimensional space. In the three-dimensional case, the basis vectors are commonly displayed as with their lengths denoted by respectively, and the angles denoted by , where conventionally, is the angle between and , is the angle between and , and is the angle between and .
Crystal Structure edit
A crystal structure is defined as the spatial distribution of the atoms within a crystal, usually modeled by the idea of an infinite crystal pattern. An infinite crystal pattern refers to the infinite 3D periodic array which corresponds to a crystal, in which the lengths of the periodicities of the array may not be made arbitrarily small. The geometrical shift which takes a crystal structure coincident with itself is termed a symmetry translation (translation) of the crystal structure. The vector which is related to this shift is called a translation vector . Since a crystal pattern is periodic, all integer linear combinations of translation vectors are also themselves translation vectors,[1]
Lattice edit
The vector lattice (lattice) is defined as the infinite set consisting of all of the translation vectors of a crystal pattern. Each of the vectors in the vector lattice are called lattice vectors. From the vector lattice it is possible to construct a point lattice. This is done by selecting an origin with position vector . The endpoints of each of the vectors make up the point lattice of and . Each point in a point lattice has periodicity i.e., each point is identical and has the same surroundings. There exist an infinite number of point lattices for a given vector lattice as any arbitrary origin can be chosen and paired with the lattice vectors of the vector lattice. The points or particles that are made coincident with one another through a translation are called translation equivalent.[1]
Coordinate systems edit
General coordinate systems edit
Usually when describing a space geometrically, a coordinate system is used which consists of a choice of origin and a basis of linearly independent, non-coplanar basis vectors , where is the dimension of the space being described. With reference to this coordinate system, each point in the space can be specified by coordinates (a coordinate -tuple). The origin has coordinates and an arbitrary point has coordinates . The position vector is then,
In -dimensions, the lengths of the basis vectors are denoted and the angles between them . However, most cases in crystallography involve two- or three-dimensional space in which the basis vectors are commonly displayed as with their lengths and angles denoted by and respectively.
Cartesian coordinate system edit
A widely used coordinate system is the Cartesian coordinate system, which consists of orthonormal basis vectors. This means that,
and
However, when describing objects with crystalline or periodic structure a Cartesian coordinate system is often not the most useful as it does not often reflect the symmetry of the lattice in the simplest manner.[1]
Fractional (crystal) coordinate system edit
In crystallography, a fractional coordinate system is used in order to better reflect the symmetry of the underlying lattice of a crystal pattern (or any other periodic pattern in space). In a fractional coordinate system the basis vectors of the coordinate system are chosen to be lattice vectors and the basis is then termed a crystallographic basis (or lattice basis).
In a lattice basis, any lattice vector can be represented as,
There are an infinite number of lattice bases for a crystal pattern. However, these can be chosen in such a way that the simplest description of the pattern can be obtained. These bases are used in the International Tables of Crystallography Volume A and are termed conventional bases. A lattice basis is called primitive if the basis vectors are lattice vectors and all lattice vectors can be expressed as,
However, the conventional basis for a crystal pattern is not always chosen to be primitive. Instead, it is chosen so the number of orthogonal basis vectors is maximized. This results in some of the coefficients of the equations above being fractional. A lattice in which the conventional basis is primitive is called a primitive lattice, while a lattice with a non-primitive conventional basis is called a centered lattice.
The choice of an origin and a basis implies the choice of a unit cell which can further be used to describe a crystal pattern. The unit cell is defined as the parallelotope (i.e., generalization of a parallelogram (2D) or parallelepiped (3D) in higher dimensions) in which the coordinates of all points are such that, .
Furthermore, points outside of the unit cell can be transformed inside of the unit cell through standardization, the addition or subtraction of integers to the coordinates of points to ensure . In a fractional coordinate system, the lengths of the basis vectors and the angles between them are called the lattice parameters (lattice constants) of the lattice. In two- and three-dimensions, these correspond to the lengths and angles between the edges of the unit cell.[1]
The fractional coordinates of a point in space in terms of the lattice basis vectors is defined as,
Calculations involving the unit cell edit
General transformations between fractional and Cartesian coordinates edit
Three Dimensions edit
The relationship between fractional and Cartesian coordinates can be described by the matrix transformation :[2]
Similarly, the Cartesian coordinates can be converted back to fractional coordinates using the matrix transformation :[2]
Transformations using the cell tensor edit
Another common method of converting between fractional and Cartesian coordinates involves the use of a cell tensor which contains each of the basis vectors of the space expressed in Cartesian coordinates.
Two Dimensions edit
Cell tensor edit
In Cartesian coordinates the 2 basis vectors are represented by a cell tensor :[3]
The area of the unit cell, , is given by the determinant of the cell matrix:
For the special case of a square or rectangular unit cell, the matrix is diagonal, and we have that:
Relationship between fractional and Cartesian coordinates edit
The relationship between fractional and Cartesian coordinates can be described by the matrix transformation :[3]
Similarly, the Cartesian coordinates can be converted back to fractional coordinates using the matrix transformation :[3]
Three Dimensions edit
Cell tensor edit
In Cartesian coordinates the 3 basis vectors are represented by a cell tensor :[3]
The volume of the unit cell, , is given by the determinant of the cell tensor:
For the special case of a cubic, tetragonal, or orthorhombic cell, the matrix is diagonal, and we have that:
Relationship between fractional and Cartesian coordinates edit
The relationship between fractional and Cartesian coordinates can be described by the matrix transformation :[3]
Similarly, the Cartesian coordinates can be converted back to fractional coordinates using the matrix transformation :[3]
Arbitrary number of dimensions edit
Cell tensor edit
In Cartesian coordinates the basis vectors are represented by a cell tensor :[3]
The hypervolume of the unit cell, , is given by the determinant of the cell tensor:
Relationship between fractional and Cartesian coordinates edit
The relationship between fractional and Cartesian coordinates can be described by the matrix transformation :[3]
Similarly, the Cartesian coordinates can be converted back to fractional coordinates using the transformation :[3]
Determination of cell properties in two and three dimensions using the metric tensor edit
The metric tensor is sometimes used for calculations involving the unit cell and is defined (in matrix form) as:[1]
In two dimensions,
In three dimensions,
The distance between two points and in the unit cell can be determined from the relation:[1]
The distance from the origin of the unit cell to a point within the unit cell can be determined from the relation:[1]
The angle formed from three points , (apex), and within the unit cell can determined from the relation:[1]
The volume of the unit cell, can be determined from the relation:[1]
References edit
- ^ a b c d e f g h i Müller, Ulrich, July 6- (2013). Symmetry relationships between crystal structures : applications of crystallographic group theory in crystal chemistry. Oxford: Oxford University Press. ISBN 978-0-19-164879-3. OCLC 850179696.
{{cite book}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - ^ a b McKie, Duncan (1986). Essentials of crystallography. Christine McKie. Oxford: Blackwell Scientific. ISBN 0-632-01566-7. OCLC 14131056.
- ^ a b c d e f g h i Alavi, Saman (2020). Molecular Simulations Fundamentals and Practice. Wiley-VCH (1. Auflage ed.). Weinheim. ISBN 978-3-527-34105-4. OCLC 1128103696.
{{cite book}}: CS1 maint: location missing publisher (link)