Ekman transport is part of Ekman motion theory, first investigated in 1902 by Vagn Walfrid Ekman. Winds are the main source of energy for ocean circulation, and Ekman transport is a component of wind-driven ocean current.[1] Ekman transport occurs when ocean surface waters are influenced by the friction force acting on them via the wind. As the wind blows it casts a friction force on the ocean surface that drags the upper 10-100m of the water column with it.[2] However, due to the influence of the Coriolis effect, the ocean water moves at a 90° angle from the direction of the surface wind.[2] The direction of transport is dependent on the hemisphere: in the northern hemisphere, transport occurs at 90° clockwise from wind direction, while in the southern hemisphere it occurs at 90° anticlockwise.[3] This phenomenon was first noted by Fridtjof Nansen, who recorded that ice transport appeared to occur at an angle to the wind direction during his Arctic expedition of the 1890s.[4] Ekman transport has significant impacts on the biogeochemical properties of the world's oceans. This is because it leads to upwelling (Ekman suction) and downwelling (Ekman pumping) in order to obey mass conservation laws. Mass conservation, in reference to Ekman transfer, requires that any water displaced within an area must be replenished. This can be done by either Ekman suction or Ekman pumping depending on wind patterns.[1]
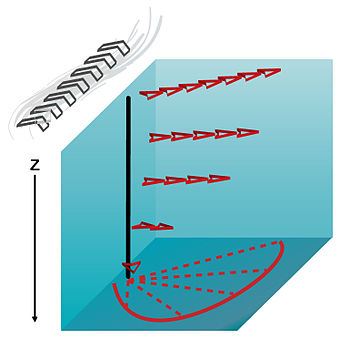
Theory edit
Ekman theory explains the theoretical state of circulation if water currents were driven only by the transfer of momentum from the wind. In the physical world, this is difficult to observe because of the influences of many simultaneous current driving forces (for example, pressure and density gradients). Though the following theory technically applies to the idealized situation involving only wind forces, Ekman motion describes the wind-driven portion of circulation seen in the surface layer.[5][6]
Surface currents flow at a 45° angle to the wind due to a balance between the Coriolis force and the drags generated by the wind and the water.[7] If the ocean is divided vertically into thin layers, the magnitude of the velocity (the speed) decreases from a maximum at the surface until it dissipates. The direction also shifts slightly across each subsequent layer (right in the northern hemisphere and left in the southern hemisphere). This is called the Ekman spiral.[8] The layer of water from the surface to the point of dissipation of this spiral is known as the Ekman layer. If all flow over the Ekman layer is integrated, the net transportation is at 90° to the right (left) of the surface wind in the northern (southern) hemisphere.[3]
Mechanisms edit
There are three major wind patterns that lead to Ekman suction or pumping. The first are wind patterns that are parallel to the coastline.[1] Due to the Coriolis effect, surface water moves at a 90° angle to the wind current. If the wind moves in a direction causing the water to be pulled away from the coast then Ekman suction will occur.[1] On the other hand, if the wind is moving in such a way that surface waters move towards the shoreline then Ekman pumping will take place.[1]
The second mechanism of wind currents resulting in Ekman transfer is the Trade Winds both north and south of the equator pulling surface waters towards the poles.[1] There is a great deal of upwelling Ekman suction at the equator because water is being pulled northward north of the equator and southward south of the equator. This leads to a divergence in the water, resulting in Ekman suction, and therefore, upwelling.[9]
The third wind pattern influencing Ekman transfer is large-scale wind patterns in the open ocean.[1] Open ocean wind circulation can lead to gyre-like structures of piled up sea surface water resulting in horizontal gradients of sea surface height.[1] This pile up of water causes the water to have a downward flow and suction, due to gravity and mass balance. Ekman pumping downward in the central ocean is a consequence of this convergence of water.[1]
Ekman suction edit
Ekman suction is the component of Ekman transport that results in areas of upwelling due to the divergence of water.[9] Returning to the concept of mass conservation, any water displaced by Ekman transport must be replenished. As the water diverges it creates space and acts as a suction in order to fill in the space by pulling up, or upwelling, deep sea water to the euphotic zone.[9]
Ekman suction has major consequences for the biogeochemical processes in the area because it leads to upwelling. Upwelling carries nutrient rich, and cold deep-sea water to the euphotic zone, promoting phytoplankton blooms and kickstarting an extremely high-productive environment.[10] Areas of upwelling lead to the promotion of fisheries, in fact nearly half of the world's fish catch comes from areas of upwelling.[11]
Ekman suction occurs both along coastlines and in the open ocean, but also occurs along the equator. Along the Pacific coastline of California, Central America, and Peru, as well as along the Atlantic coastline of Africa there are areas of upwelling due to Ekman suction, as the currents move equatorwards.[1] Due to the Coriolis effect the surface water moves 90° to the left (in the South Hemisphere, as it travels toward the equator) of the wind current, therefore causing the water to diverge from the coast boundary, leading to Ekman suction. Additionally, there are areas of upwelling as a consequence of Ekman suction where the Polar Easterlies winds meet the Westerlies in the subpolar regions north of the subtropics, as well as where the Northeast Trade Winds meet the Southeast Trade Winds along the Equator.[1] Similarly, due to the Coriolis effect the surface water moves 90° to the left (in the South Hemisphere) of the wind currents, and the surface water diverges along these boundaries, resulting in upwelling in order to conserve mass.
Ekman pumping edit
Ekman pumping is the component of Ekman transport that results in areas of downwelling due to the convergence of water.[9] As discussed above, the concept of mass conservation requires that a pile up of surface water must be pushed downward. This pile up of warm, nutrient-poor surface water gets pumped vertically down the water column, resulting in areas of downwelling.[1]
Ekman pumping has dramatic impacts on the surrounding environments. Downwelling, due to Ekman pumping, leads to nutrient poor waters, therefore reducing the biological productivity of the area.[11] Additionally, it transports heat and dissolved oxygen vertically down the water column as warm oxygen rich surface water is being pumped towards the deep ocean water.[11]
Ekman pumping can be found along the coasts as well as in the open ocean. Along the Pacific Coast in the Southern Hemisphere northerly winds move parallel to the coastline.[1] Due to the Coriolis effect the surface water gets pulled 90° to the left of the wind current, therefore causing the water to converge along the coast boundary, leading to Ekman pumping. In the open ocean Ekman pumping occurs with gyres.[1] Specifically, in the subtropics, between 20°N and 50°N, there is Ekman pumping as the tradewinds shift to westerlies causing a pile up of surface water.[1]
Mathematical derivation edit
Some assumptions of the fluid dynamics involved in the process must be made in order to simplify the process to a point where it is solvable. The assumptions made by Ekman were:[12]
- no boundaries;
- infinitely deep water;
- eddy viscosity, , is constant (this is only true for laminar flow. In the turbulent atmospheric and oceanic boundary layer it is a strong function of depth);
- the wind forcing is steady and has been blowing for a long time;
- barotropic conditions with no geostrophic flow;
- the Coriolis parameter, is kept constant.
The simplified equations for the Coriolis force in the x and y directions follow from these assumptions:
- (1)
- (2)
where is the wind stress, is the density, is the east–west velocity, and is the north–south velocity.
Integrating each equation over the entire Ekman layer:
where
Here and represent the zonal and meridional mass transport terms with units of mass per unit time per unit length. Contrarily to common logic, north–south winds cause mass transport in the east–west direction.[13]
In order to understand the vertical velocity structure of the water column, equations 1 and 2 can be rewritten in terms of the vertical eddy viscosity term.
where is the vertical eddy viscosity coefficient.
This gives a set of differential equations of the form
In order to solve this system of two differential equations, two boundary conditions can be applied:
- as
- friction is equal to wind stress at the free surface ( ).
Things can be further simplified by considering wind blowing in the y-direction only. This means is the results will be relative to a north–south wind (although these solutions could be produced relative to wind in any other direction):[14]
- (3)
where
- and represent Ekman transport in the u and v direction;
- in equation 3 the plus sign applies to the northern hemisphere and the minus sign to the southern hemisphere;
- is the wind stress on the sea surface;
- is the Ekman depth (depth of Ekman layer).
By solving this at z=0, the surface current is found to be (as expected) 45 degrees to the right (left) of the wind in the Northern (Southern) Hemisphere. This also gives the expected shape of the Ekman spiral, both in magnitude and direction.[14] Integrating these equations over the Ekman layer shows that the net Ekman transport term is 90 degrees to the right (left) of the wind in the Northern (Southern) Hemisphere.
Applications edit
- Ekman transport leads to coastal upwelling, which provides the nutrient supply for some of the largest fishing markets on the planet[15] and can impact the stability of the Antarctic Ice Sheet by pulling warm deep water onto the continental shelf.[16][17] Wind in these regimes blows parallel to the coast (such as along the coast of Peru, where the wind blows out of the southeast, and also in California, where it blows out of the northwest). From Ekman transport, surface water has a net movement of 90° to right of wind direction in the northern hemisphere (left in the southern hemisphere). Because the surface water flows away from the coast, the water must be replaced with water from below.[18] In shallow coastal waters, the Ekman spiral is normally not fully formed and the wind events that cause upwelling episodes are typically rather short. This leads to many variations in the extent of upwelling, but the ideas are still generally applicable.[19]
- Ekman transport is similarly at work in equatorial upwelling, where, in both hemispheres, a trade wind component towards the west causes a net transport of water towards the pole, and a trade wind component towards the east causes a net transport of water away from the pole.[15]
- On smaller scales, cyclonic winds induce Ekman transport which causes net divergence and upwelling, or Ekman suction,[15] while anti-cyclonic winds cause net convergence and downwelling, or Ekman pumping[20]
- Ekman transport is also a factor in the circulation of the ocean gyres and garbage patches. Ekman transport causes water to flow toward the center of the gyre in all locations, creating a sloped sea-surface, and initiating geostrophic flow (Colling p 65). Harald Sverdrup applied Ekman transport while including pressure gradient forces to develop a theory for this (see Sverdrup balance).[20]
See also edit
- Ekman velocity – Formula for wind induced water current velocity
Notes edit
- ^ a b c d e f g h i j k l m n o Sarmiento, Jorge L.; Gruber, Nicolas (2006). Ocean biogeochemical dynamics. Princeton University Press. ISBN 978-0-691-01707-5.
- ^ a b Emerson, Steven R.; Hedges, John I. (2017). Chemical Oceanography and the Marine Carbon Cycle. New York, United States of America: Cambridge University Press. ISBN 978-0-521-83313-4.
- ^ a b Colling, pp 42-44
- ^ Pond & Pickard, p 101
- ^ Colling p 44
- ^ Sverdrup p 228
- ^ Mann & Lazier p 169
- ^ Knauss p 124.
- ^ a b c d Emerson, Steven R.; Hedges, John I. (2017). Chemical oceanography and the marine carbon cycle. New York, United States of America: Cambridge University Press. ISBN 978-0-521-83313-4.
- ^ Miller, Charles B.; Wheeler, Patricia A. (2012-05-21). Biological Oceanography (Second ed.). Wiley-Blackwell. ISBN 978-1-4443-3302-2.
- ^ a b c Lindstrom, Eric J. "Ocean Motion : Definition : Wind Driven Surface Currents - Upwelling and Downwelling". oceanmotion.org.
- ^ Pond & Pickard p. 106
- ^ Knauss p. 123
- ^ a b Pond & Pickard p.108
- ^ a b c Knauss p 125
- ^ Anderson, R. F.; Ali, S.; Bradtmiller, L. I.; Nielsen, S. H. H.; Fleisher, M. Q.; Anderson, B. E.; Burckle, L. H. (2009-03-13). "Wind-Driven Upwelling in the Southern Ocean and the Deglacial Rise in Atmospheric CO2". Science. 323 (5920): 1443–1448. Bibcode:2009Sci...323.1443A. doi:10.1126/science.1167441. ISSN 0036-8075. PMID 19286547. S2CID 206517043.
- ^ Greene, Chad A.; Blankenship, Donald D.; Gwyther, David E.; Silvano, Alessandro; Wijk, Esmee van (2017-11-01). "Wind causes Totten Ice Shelf melt and acceleration". Science Advances. 3 (11): e1701681. Bibcode:2017SciA....3E1681G. doi:10.1126/sciadv.1701681. ISSN 2375-2548. PMC 5665591. PMID 29109976.
- ^ Mann & Lazier p 172
- ^ Colling p 43
- ^ a b Pond & Pickard p 295
References edit
- Colling, A., Ocean Circulation, Open University Course Team. Second Edition. 2001. ISBN 978-0-7506-5278-0
- Emerson, Steven R.; Hedges, John I. (2017). Chemical Oceanography and the Marine Carbon Cycle. New York, United States of America: Cambridge University Press. ISBN 978-0-521-83313-4.
- Knauss, J.A., Introduction to Physical Oceanography, Waveland Press. Second Edition. 2005. ISBN 978-1-57766-429-1
- Lindstrom, Eric J. "Ocean Motion : Definition : Wind Driven Surface Currents - Upwelling and Downwelling". oceanmotion.org.
- Mann, K.H. and Lazier J.R., Dynamics of Marine Ecosystems, Blackwell Publishing. Third Edition. 2006. ISBN 978-1-4051-1118-8
- Miller, Charles B.; Wheeler, Patricia A. Biological Oceanography (Second ed.). Wiley-Blackwell. ISBN 978-1-4443-3302-2.
- Pond, S. and Pickard, G. L., Introductory Dynamical Oceanography, Pergamon Press. Second edition. 1983. ISBN 978-0-08-028728-7
- Sarmiento, Jorge L.; Gruber, Nicolas (2006). Ocean biogeochemical dynamics. Princeton University Press. ISBN 978-0-691-01707-5.
- Sverdrup, K.A., Duxbury, A.C., Duxbury, A.B., An Introduction to The World's Oceans, McGraw-Hill. Eighth Edition. 2005. ISBN 978-0-07-294555-3