Complex torus

In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense (i.e. the cartesian product of some number N circles). Here N must be the even number 2n, where n is the complex dimension of M.

The complex torus associated to a lattice spanned by two periods, ω₁ and ω₂. Corresponding edges are identified.

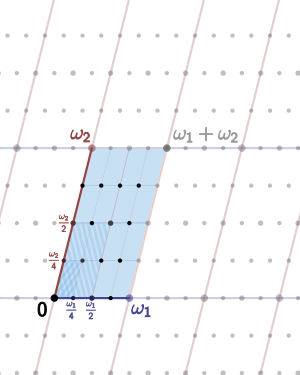
All such complex structures can be obtained as follows: take a lattice Λ in a vector space V isomorphic to Cⁿ considered as real vector space; then the quotient group

$$V/\Lambda$$

is a compact complex manifold. All complex tori, up to isomorphism, are obtained in this way. For n = 1 this is the classical period lattice construction of elliptic curves. For n > 1 Bernhard Riemann found necessary and sufficient conditions for a complex torus to be an algebraic variety; those that are varieties can be embedded into complex projective space, and are the abelian varieties.

The actual projective embeddings are complicated (see equations defining abelian varieties) when n > 1, and are really coextensive with the theory of theta-functions of several complex variables (with fixed modulus). There is nothing as simple as the cubic curve description for n = 1. Computer algebra can handle cases for small n reasonably well. By Chow's theorem, no complex torus other than the abelian varieties can 'fit' into projective space.

Definition

One way to define complex tori is as a compact connected complex Lie group $G$. These are Lie groups where the structure maps are holomorphic maps of complex manifolds. It turns out that all such compact connected Lie groups are commutative, and are isomorphic to a quotient of their Lie algebra ${\mathfrak {g}}=T_{0}G$ whose covering map is the exponential map of a Lie algebra to its associated Lie group. The kernel of this map is a lattice $\Lambda \subset {\mathfrak {g}}$ and ${\mathfrak {g}}/\Lambda \cong U$.

Conversely, given a complex vector space $V$ and a lattice $\Lambda \subseteq V$ of maximal rank, the quotient complex manifold $V/\Lambda$ has a complex Lie group structure, and is also compact and connected. This implies the two definitions for complex tori are equivalent.

Period matrix of a complex torus

One way to describe a g-dimensional complex torus is by using a $g\times 2g$ matrix $\Pi$ whose columns correspond to a basis $\lambda _{1},\ldots ,\lambda _{2g}$ of the lattice $\Lambda$ expanded out using a basis $e_{1},\ldots ,e_{g}$ of $V$. That is, we write

$$\Pi ={\begin{pmatrix}\lambda _{1,1}&\cdots &\lambda _{1,2g}\\\vdots &&\vdots \\\lambda _{g,1}&\cdots &\lambda _{g,2g}\end{pmatrix}}$$

so

$$\lambda _{i}=\sum _{j}\lambda _{ji}e_{j}$$

We can then write the torus $X=V/\Lambda$ as

$$X=\mathbb {C} ^{g}/\Pi \mathbb {Z} ^{2g}$$

If we go in the reverse direction by selecting a matrix $\Pi \in Mat_{\mathbb {C} }(g,2g)$, it corresponds to a period matrix if and only if the corresponding matrix $P\in Mat_{\mathbb {C} }(2g,2g)$ constructed by adjoining the complex conjugate matrix ${\overline {\Pi }}$ to $\Pi$, so

$$P={\begin{pmatrix}\Pi \\{\overline {\Pi }}\end{pmatrix}}$$

is nonsingular. This guarantees the column vectors of $\Pi$ span a lattice in $\mathbb {C} ^{g}$ hence must be linearly independent vectors over $\mathbb {R}$.

Example

For a two-dimensional complex torus, it has a period matrix of the form

$$\Pi ={\begin{pmatrix}\lambda _{1,1}&\lambda _{1,2}&\lambda _{1,3}&\lambda _{1,4}\\\lambda _{2,1}&\lambda _{2,2}&\lambda _{2,3}&\lambda _{2,4}\end{pmatrix}}$$

for example, the matrix

$$\Pi ={\begin{pmatrix}1&0&i&2i\\1&-i&1&1\end{pmatrix}}$$

forms a period matrix since the associated period matrix has determinant 4.

Normalized period matrix

For any complex torus $X=V/\Lambda$ of dimension $g$ it has a period matrix $\Pi$ of the form

$$(Z,1_{g})$$

where $1_{g}$ is the identity matrix and $Z\in Mat_{\mathbb {C} }(g)$ where $\det {\text{Im}}(Z)\neq 0$. We can get this from taking a change of basis of the vector space $V$ giving a block matrix of the form above. The condition for $\det {\text{Im}}(Z)\neq 0$ follows from looking at the corresponding $P$-matrix

$${\begin{pmatrix}Z&1_{g}\\{\overline {Z}}&1_{g}\end{pmatrix}}$$

since this must be a non-singular matrix. This is because if we calculate the determinant of the block matrix, this is simply

$${\begin{aligned}\det P&=\det(1_{g})\det(Z-1_{g}1_{g}{\overline {Z}})\\&=\det(Z-{\overline {Z}})\\&\Rightarrow \det({\text{Im}}(Z))\neq 0\end{aligned}}$$

which gives the implication.

Example

For example, we can write a normalized period matrix for a 2-dimensional complex torus as

$${\begin{pmatrix}z_{1,1}&z_{1,2}&1&0\\z_{2,1}&z_{2,2}&0&1\end{pmatrix}}$$

one such example is the normalized period matrix

$${\begin{pmatrix}1+i&1-i&1&0\\1+2i&1+{\sqrt {2}}i&0&1\end{pmatrix}}$$

since the determinant of ${\text{Im}}(Z)$ is nonzero, equal to $2+{\sqrt {2}}$.

Period matrices of Abelian varieties

To get a period matrix which gives a projective complex manifold, hence an algebraic variety, the period matrix needs to further satisfy the Riemann bilinear relations.

Homomorphisms of complex tori

If we have complex tori $X=V/\Lambda$ and $X'=V'/\Lambda '$ of dimensions $g,g'$ then a homomorphism of complex tori is a function

$$f:X\to X'$$

such that the group structure is preserved. This has a number of consequences, such as every homomorphism induces a map of their covering spaces

$$F:V\to V'$$

which is compatible with their covering maps. Furthermore, because $F$ induces a group homomorphism, it must restrict to a morphism of the lattices

$$F_{\Lambda }:\Lambda \to \Lambda '$$

In particular, there are injections

$$\rho _{a}:{\text{Hom}}(X,X')\to {\text{Hom}}_{\mathbb {C} }(V,V')$$

and $\rho _{r}:{\text{Hom}}(X,X')\to {\text{Hom}}_{\mathbb {Z} }(\Lambda ,\Lambda ')$ which are called the analytic and rational representations of the space of homomorphisms. These are useful to determining some information about the endomorphism ring ${\text{End}}(X)\otimes \mathbb {Q}$ which has rational dimension $m\leq 4gg'$.

Holomorphic maps of complex tori

The class of homomorphic maps between complex tori have a very simple structure. Of course, every homomorphism induces a holomorphic map, but every holomorphic map is the composition of a special kind of holomorphic map with a homomorphism. For an element $x_{0}\in X$ we define the translation map

$$t_{x_{0}}:X\to X$$

sending $x\mapsto x+x_{0}$ Then, if $h$ is a holomorphic map between complex tori $X,X'$, there is a unique homomorphism $f:X\to X'$ such that

$$h=t_{h(0)}\circ f$$

showing the holomorphic maps are not much larger than the set of homomorphisms of complex tori.

Isogenies

One distinct class of homomorphisms of complex tori are called isogenies. These are endomorphisms of complex tori with a non-zero kernel. For example, if we let $n\in \mathbb {Z} _{\neq 0}$ be an integer, then there is an associated map

$$n_{X}:X\to X$$

sending $x\mapsto nx$ which has kernel

$$X_{n}\cong (\mathbb {Z} /n\mathbb {Z} )^{2g}$$

isomorphic to $\Lambda /n\Lambda$.

Isomorphic complex tori

There is an isomorphism of complex structures on the real vector space $\mathbb {R} ^{2g}$ and the set

$$GL_{\mathbb {R} }(2g)/GL_{\mathbb {C} }(g)$$

and isomorphic tori can be given by a change of basis of their lattices, hence a matrix in $GL_{\mathbb {Z} }(2g)$. This gives the set of isomorphism classes of complex tori of dimension $g$, ${\mathcal {T}}_{g}$, as the Double coset space

$${\mathcal {T}}_{g}\cong GL_{\mathbb {Z} }(2g)\backslash GL_{\mathbb {R} }(2g)/GL_{\mathbb {C} }(g)$$

Note that as a real manifold, this has dimension

$$4g^{2}-2g^{2}=2g^{2}$$

this is important when considering the dimensions of moduli of Abelian varieties, which shows there are far more complex tori than Abelian varieties.

Line bundles and automorphic forms

For complex manifolds $X$, in particular complex tori, there is a construction relating the holomorphic line bundles $L\to X$ whose pullback $\pi ^{*}L\to {\tilde {X}}$ are trivial using the group cohomology of $\pi _{1}(X)$. Fortunately for complex tori, every complex line bundle $\pi ^{*}L$ becomes trivial since ${\tilde {X}}\cong \mathbb {C} ^{n}$.

Factors of automorphy

Starting from the first group cohomology group

$$H^{1}(\pi _{1}(X),H^{0}({\mathcal {O}}_{\tilde {X}}^{*}))$$

we recall how its elements can be represented. Since $\pi _{1}(X)$ acts on ${\tilde {X}}$ there is an induced action on all of its sheaves, hence on

$$H^{0}({\mathcal {O}}_{\tilde {X}}^{*})=\{f:{\tilde {X}}\to \mathbb {C} ^{*}\}$$

The $\pi _{1}(X)$-action can then be represented as a holomorphic map $f:\pi _{1}(X)\times {\tilde {X}}\to \mathbb {C} ^{*}$. This map satisfies the cocycle condition if

$$f(a\cdot b,x)=f(a,b\cdot x)f(b,x)$$

for every $a,b\in \pi _{1}(X)$ and $x\in {\tilde {X}}$. The abelian group of 1-cocycles $Z^{1}(\pi _{1}(X),H^{0}({\mathcal {O}}_{\tilde {X}}^{*}))$ is called the group of factors of automorphy. Note that such functions $f$ are also just called factors.

On complex tori

For complex tori, these functions $f$ are given by functions

$$f:\mathbb {C} ^{n}\times \mathbb {Z} ^{2n}\to \mathbb {C} ^{*}$$

which follow the cocycle condition. These are automorphic functions, more precisely, the automorphic functions used in the transformation laws for theta functions. Also, any such map can be written as

$$f=\exp(2\pi i\cdot g)$$

for

$$g:V\times \Lambda \to \mathbb {C}$$

which is useful for computing invariants related to the associated line bundle.

Line bundles from factors of automorphy

Given a factor of automorphy $f$ we can define a line bundle on $X$ as follows: the trivial line bundle ${\tilde {X}}\times \mathbb {C} \to {\tilde {X}}$ has a $\pi _{1}(X)$-action given by

$$a\cdot (x,t)=(a\cdot x,f(a,x)\cdot t)$$

for the factor $f$. Since this action is free and properly discontinuous, the quotient bundle

$$L={\tilde {X}}\times \mathbb {C} /\pi _{1}(X)$$

is a complex manifold. Furthermore, the projection $p:L\to X$ induced from the covering projection $\pi :{\tilde {X}}\to X$. This gives a map

$$Z^{1}(\pi _{1}(X),H^{0}({\mathcal {O}}_{\tilde {X}}^{*}))\to H^{1}(X,{\mathcal {O}}_{X}^{*})$$

which induces an isomorphism

$$H^{1}(\pi _{1}(X),H^{0}({\mathcal {O}}_{\tilde {X}}^{*}))\to \ker(H^{1}(X,{\mathcal {O}}_{X}^{*})\to H^{1}({\tilde {X}},{\mathcal {O}}_{\tilde {X}}^{*}))$$

giving the desired result.

For complex tori

In the case of complex tori, we have $H^{1}({\tilde {X}},{\mathcal {O}}_{\tilde {X}}^{*})\cong 0$ hence there is an isomorphism

$$H^{1}(\pi _{1}(X),H^{0}({\mathcal {O}}_{\tilde {X}}^{*}))\cong H^{1}(X,{\mathcal {O}}_{X}^{*})$$

representing line bundles on complex tori as 1-cocyles in the associated group cohomology. It is typical to write down the group $\pi _{1}(X)$ as the lattice $\Lambda$ defining $X$, hence

$$H^{1}(\Lambda ,H^{0}({\mathcal {O}}_{V}^{*}))$$

contains the isomorphism classes of line bundles on $X$.

First chern class of line bundles on complex tori

From the exponential exact sequence

$$0\to \mathbb {Z} \to {\mathcal {O}}_{X}\to {\mathcal {O}}_{X}^{*}\to 0$$

the connecting morphism

$$c_{1}:H^{1}({\mathcal {O}}_{X}^{*})\to H^{2}(X,\mathbb {Z} )$$

is the first Chern class map, sending an isomorphism class of a line bundle to its associated first Chern class. It turns out there is an isomorphism between $H^{2}(X,\mathbb {Z} )$ and the module of alternating forms on the lattice $\Lambda$, $Alt^{2}(\Lambda ,\mathbb {Z} )$. Therefore, $c_{1}(L)$ can be considered as an alternating $\mathbb {Z}$-valued 2-form $E_{L}$ on $\Lambda$. If $L$ has factor of automorphy $f=\exp(2\pi ig)$ then the alternating form can be expressed as

$$E_{L}(\lambda ,\mu )=g(\mu ,v+\lambda )+g(\lambda ,v)-g(\lambda ,v+\mu )-g(\mu ,v)$$

for $\mu ,\lambda \in \Lambda$ and $v\in V$.

Example

For a normalized period matrix

$$\Pi ={\begin{pmatrix}z_{1,1}&z_{1,2}&1&0\\z_{2,1}&z_{2,2}&0&1\end{pmatrix}}$$

expanded using the standard basis of $\mathbb {C} ^{2}$ we have the column vectors defining the lattice $\Lambda \subset \mathbb {C} ^{2}$. Then, any alternating form $E_{L}$ on $\Lambda$ is of the form

$$E_{L}={\begin{pmatrix}0&e_{2,1}&e_{3,1}&e_{4,1}\\-e_{2,1}&0&e_{3,2}&e_{4,2}\\-e_{3,1}&-e_{2,3}&0&e_{4,3}\\-e_{4,1}&-e_{4,2}&-e_{4,3}&0\end{pmatrix}}$$

where a number of compatibility conditions must be satisfied.

Sections of line bundles and theta functions

For a line bundle $L$ given by a factor of automorphy $f:\Lambda \times V\to \mathbb {C} ^{*}$, so $[f]\in H^{1}(\Lambda ,H^{0}(V,{\mathcal {O}}_{V}^{*}))$ and $\phi _{1}[f]=[L]\in {\text{Pic}}(X)$, there is an associated sheaf of sections ${\mathcal {L}}$ where

$${\mathcal {L}}(U)=\left\{\theta :\pi ^{-1}(U)\to \mathbb {C} :{\begin{matrix}\theta {\text{ holomorphic with }}\theta (v+\lambda )=f(\lambda ,v)\theta (v)\\{\text{for all }}(\lambda ,v)\in \Lambda \times \pi ^{-1}(U)\end{matrix}}\right\}$$

with $U\subset X$ open. Then, evaluated on global sections, this is the set of holomorphic functions $\theta :V\to \mathbb {C}$ such that

$$\theta (v+\lambda )=f(\lambda ,v)\theta (v)$$

which are exactly the theta functions on the plane. Conversely, this process can be done backwards where the automorphic factor in the theta function is in fact the factor of automorphy defining a line bundle on a complex torus.

Hermitian forms and the Appell-Humbert theorem

See also: Appell–Humbert theorem

For the alternating $\mathbb {Z}$-valued 2-form $E_{L}$ associated to the line bundle $L\to X$, it can be extended to be $\mathbb {R}$-valued. Then, it turns out any $\mathbb {R}$-valued alternating form $E:V\times V\to \mathbb {R}$ satisfying the following conditions

1. $E(\Lambda ,\Lambda )\subseteq \mathbb {Z}$
2. $E(iv,iw)=E(v,w)$ for any $v,w\in V$

is the extension of some first Chern class $c_{1}(L)$ of a line bundle $L\to X$. Moreover, there is an associated Hermitian form $H:V\times V\to \mathbb {C}$ satisfying

1. ${\text{Im}}H(v,w)=E(v,w)$
2. $H(v,w)=E(iv,w)+iE(v,w)$

for any $v,w\in V$.

Neron-Severi group

See also: Néron–Severi group

For a complex torus $X=V/\Lambda$ we can define the Neron-Serveri group $NS(X)$ as the group of Hermitian forms $H$ on $V$ with

$${\text{Im}}H(\Lambda ,\Lambda )\subseteq \mathbb {Z}$$

Equivalently, it is the image of the homomorphism

$$c_{1}:H^{1}({\mathcal {O}}_{X}^{*})\to H^{2}(X,\mathbb {Z} )$$

from the first Chern class. We can also identify it with the group of alternating real-valued alternating forms $E$ on $V$ such that $E(\Lambda ,\Lambda )\subseteq \mathbb {Z}$.

Example of a Hermitian form on an elliptic curve

For an elliptic curve ${\mathcal {E}}$ given by the lattice ${\begin{pmatrix}1&\tau \end{pmatrix}}$ where $\tau \in \mathbb {H}$ we can find the integral form $E\in {\text{Alt}}^{2}(\Lambda ,\mathbb {Z} )$ by looking at a generic alternating matrix and finding the correct compatibility conditions for it to behave as expected. If we use the standard basis $x_{1},y_{1}$ of $\mathbb {C}$ as a real vector space (so $z=z_{1}+iz_{2}=z_{1}x_{1}+z_{2}y_{1}$), then we can write out an alternating matrix

$$E={\begin{pmatrix}0&e\\-e&0\end{pmatrix}}$$

and calculate the associated products on the vectors associated to $1,\tau$. These are

$${\begin{aligned}E\cdot {\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}0\\-e\end{pmatrix}}&&E\cdot {\begin{pmatrix}\tau _{1}\\\tau _{2}\end{pmatrix}}={\begin{pmatrix}e\tau _{2}\\-e\tau _{1}\end{pmatrix}}\end{aligned}}$$

Then, taking the inner products (with the standard inner product) of these vectors with the vectors $1,\tau$ we get

$${\begin{aligned}{\begin{pmatrix}1\\0\end{pmatrix}}\cdot {\begin{pmatrix}0\\-e\end{pmatrix}}=0&&{\begin{pmatrix}\tau _{1}\\\tau _{2}\end{pmatrix}}\cdot {\begin{pmatrix}0\\-e\end{pmatrix}}=-e\tau _{2}\\{\begin{pmatrix}1\\0\end{pmatrix}}\cdot {\begin{pmatrix}e\tau _{2}\\-e\tau _{1}\end{pmatrix}}=e\tau _{2}&&{\begin{pmatrix}\tau _{1}\\\tau _{2}\end{pmatrix}}\cdot {\begin{pmatrix}e\tau _{2}\\-e\tau _{1}\end{pmatrix}}=0\end{aligned}}$$

so if $E(\Lambda ,\Lambda )\subset \mathbb {Z}$, then

$$e=a{\frac {1}{{\text{Im}}(\tau )}}$$

We can then directly verify $E(v,w)=E(iv,iw)$, which holds for the matrix above. For a fixed $a$, we will write the integral form as $E_{a}$. Then, there is an associated Hermitian form

$$H_{a}:\mathbb {C} \times \mathbb {C} \to \mathbb {C}$$

given by

$$H_{a}(z,w)=a\cdot {\frac {z{\overline {w}}}{{\text{Im}}(\tau )}}$$

where $a\in \mathbb {Z}$

Semi-character pairs for Hermitian forms

For a Hermitian form $H$ a semi-character is a map $\chi :\Lambda \to U(1)$ such that

$$\chi (\lambda +\mu )=\chi (\lambda )\chi (\mu )\exp(i\pi {\text{Im}}H(\lambda ,\mu ))$$

hence the map $\chi$ behaves like a character twisted by the Hermitian form. Note that if $H$ is the zero element in $NS(X)$, so it corresponds to the trivial line bundle $\mathbb {C} \times X\to X$, then the associated semi-characters are the group of characters on $\Lambda$. It will turn out this corresponds to the group ${\text{Pic}}^{0}(X)$ of degree $0$ line bundles on $X$, or equivalently, its dual torus, which can be seen by computing the group of characters ${\text{Hom}}(\Lambda ,U(1))$ whose elements can be factored as maps $\Lambda \to \mathbb {R} \to \mathbb {R} /\mathbb {Z} \cong U(1)$ showing a character is of the form $\chi (\cdot )=\exp \left(2\pi iv^{*}(\cdot )\right)$ for some fixed dual lattice vector $v^{*}\in \Lambda ^{*}$. This gives the isomorphism ${\text{Hom}}(\Lambda ,U(1))\cong \mathbb {R} ^{2g}/\mathbb {Z} ^{2g}$ of the set of characters with a real torus. The set of all pairs of semi-characters and their associated Hermitian form $(\chi ,H)$, or semi-character pairs, forms a group ${\mathcal {P}}(\Lambda )$ where

$$(H_{1},\chi _{1})*(H_{2},\chi _{2})=(H_{1}+H_{2},\chi _{1}\chi _{2})$$

This group structure comes from applying the previous commutation law for semi-characters to the new semicharacter $\chi _{1}\chi _{2}$:

$${\begin{aligned}\chi _{1}\chi _{2}(\lambda +\mu )&=\chi _{1}(\lambda +\mu )\chi _{2}(\lambda +\mu )\\&=\chi _{1}(\lambda )\chi _{1}(\mu )\chi _{2}(\lambda )\chi _{2}(\mu )\exp(i\pi {\text{Im}}H_{1}(\lambda ,\mu ))\exp(i\pi {\text{Im}}H_{2}(\lambda ,\mu ))\\&=\chi _{1}\chi _{2}(\lambda )\chi _{1}\chi _{2}(\mu )\exp(i\pi {\text{Im}}H_{1}(\lambda ,\mu )+i\pi {\text{Im}}H_{2}(\lambda ,\mu ))\end{aligned}}$$

It turns out this group surjects onto $NS(X)$ and has kernel ${\text{Hom}}(\Lambda ,U(1))$, giving a short exact sequence

$$1\to {\text{Hom}}(\Lambda ,U(1))\to {\mathcal {P}}(\Lambda )\to NS(X)\to 1$$

This surjection can be constructed through associating to every semi-character pair a line bundle $L(H,\chi )$.

Semi-character pairs and line bundles

For a semi-character pair $(H,\chi )$ we can construct a 1-cocycle $a_{(H,\chi )}$ on $\Lambda$ as a map

$$a_{(H,\chi )}:\Lambda \times V\to \mathbb {C} ^{*}$$

defined as

$$a(\lambda ,v)=\chi (\lambda )\exp(\pi H(v,\lambda )+{\frac {\pi }{2}}H(\lambda ,\lambda ))$$

The cocycle relation

$$a(\lambda +\mu ,v)=a(\lambda ,v+\mu )a(\mu ,v)$$

can be easily verified by direct computation. Hence the cocycle determines a line bundle

$$L(H,\chi )\cong V\times \mathbb {C} /\Lambda$$

where the $\Lambda$-action on $V\times \mathbb {C}$ is given by

$$\lambda \circ (v,t)=(v+t,a_{(H,\chi )}(\lambda ,v)t)$$

Note this action can be used to show the sections of the line bundle $L(H,\chi )$ are given by the theta functions with factor of automorphy $a_{(H,\chi )}$. Sometimes, this is called the canonical factor of automorphy for $L$. Note that because every line bundle $L\to X$ has an associated Hermitian form $H$, and a semi-character can be constructed using the factor of automorphy for $L$, we get a surjection

$${\mathcal {P}}(\Lambda )\to {\text{Pic}}(X)$$

Moreover, this is a group homomorphism with a trivial kernel. These facts can all be summarized in the following commutative diagram

$${\begin{matrix}1&\to &{\text{Hom}}(\Lambda ,U(1))&\to &{\mathcal {P}}(\Lambda )&\to &NS(X)&\to 0\\&&\downarrow &&\downarrow &&\downarrow \\1&\to &{\text{Pic}}^{0}(X)&\to &{\text{Pic}}(X)&\to &{\text{NS}}(X)&\to 0\end{matrix}}$$

where the vertical arrows are isomorphisms, or equality. This diagram is typically called the Appell-Humbert theorem.

Dual complex torus

See also: Poincare bundle and Dual abelian variety

As mentioned before, a character on the lattice can be expressed as a function

$$\chi (\cdot )=\exp \left(2\pi iv^{*}(\cdot )\right)$$

for some fixed dual vector $v^{*}\in \Lambda ^{*}$. If we want to put a complex structure on the real torus of all characters, we need to start with a complex vector space which $\Lambda ^{*}$ embeds into. It turns out that the complex vector space

$${\overline {\Omega }}={\text{Hom}}_{\overline {\mathbb {C} }}(V,\mathbb {C} )$$

of complex antilinear maps, is isomorphic to the real dual vector space ${\text{Hom}}_{\mathbb {R} }(V,\mathbb {R} )$, which is part of the factorization for writing down characters. Furthermore, there is an associated lattice

$${\hat {\Lambda }}=\{l\in {\overline {\Omega }}:\langle l,\Lambda \rangle \subseteq \mathbb {Z} \}$$

called the dual lattice of $\Lambda$. Then, we can form the dual complex torus

$${\hat {X}}\cong {\overline {\Omega }}/{\hat {\Lambda }}$$

which has the special property that that dual of the dual complex torus is the original complex torus. Moreover, from the discussion above, we can identify the dual complex torus with the Picard group of $X$

$${\hat {X}}\cong {\text{Pic}}^{0}(X)$$

by sending an anti-linear dual vector $l$ to

$$l\mapsto \exp(2\pi i\langle l,\cdot \rangle )$$

giving the map

$${\overline {\Omega }}\to {\text{Hom}}(\Lambda ,U(1))$$

which factors through the dual complex torus. There are other constructions of the dual complex torus using techniques from the theory of Abelian varieties. Essentially, taking a line bundle $L$ over a complex torus (or Abelian variety) $X$, there is a closed subset $K(L)$ of $X$ defined as the points of $x\in X$ where their translations are invariant, i.e.

$$T_{x}^{*}(L)\cong L$$

Then, the dual complex torus can be constructed as

$${\hat {X}}:=X/K(L)$$

presenting it as an isogeny. It can be shown that defining ${\hat {X}}$ this way satisfied the universal properties of ${\text{Pic}}^{0}(X)$, hence is in fact the dual complex torus (or Abelian variety).

Poincare bundle

From the construction of the dual complex torus, it is suggested there should exist a line bundle ${\mathcal {P}}$ over the product of the torus $X$ and its dual which can be used to present all isomorphism classes of degree 0 line bundles on $X$. We can encode this behavior with the following two properties

1. ${\mathcal {P}}|_{X\times \{[L]\}}\cong L$ for any point $[L]\in {\hat {X}}$ giving the line bundle $L$
2. ${\mathcal {P}}|_{\{0\}\times {\hat {X}}}$ is a trivial line bundle

where the first is the property discussed above, and the second acts as a normalization property. We can construct ${\mathcal {P}}$ using the following hermitian form

$${\begin{matrix}H:(V\times {\overline {\Omega }})\times (V\times {\overline {\Omega }})\to \mathbb {C} \\H((v_{1},l_{1}),(v_{2},l_{2}))={\overline {l_{2}(v_{1})}}+l_{1}(v_{2})\end{matrix}}$$

and the semi-character

$${\begin{matrix}\chi :\Lambda \times {\hat {\Lambda }}\to U(1)\\\chi (\lambda ,l_{0})=\exp(i\pi {\text{Im}}l_{0}(\lambda ))\end{matrix}}$$

for $H$. Showing this data constructs a line bundle with the desired properties follows from looking at the associated canonical factor of $(H,\chi )$, and observing its behavior at various restrictions.

See also

• Poincare bundle
• Complex Lie group
• Automorphic function
• Intermediate Jacobian
• Elliptic gamma function

References

• Birkenhake, Christina; Lange, Herbert (1999), Complex tori, Progress in Mathematics, vol. 177, Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4103-0, MR 1713785

Complex 2-dimensional tori

• Ruppert, Wolfgang M. (1990). "When is an abelian surface isomorphic or isogeneous to a product of elliptic curves?". Mathematische Zeitschrift. 203: 293–299. doi:10.1007/BF02570737. S2CID 120799085. - Gives tools to find complex tori which are not Abelian varieties
• Marchisio, Marina Rosanna (1998). "Abelian surfaces and products of elliptic curves". Bollettino dell'unione Matematica Italiana. 1-B (2): 407–427.

Gerbes on complex tori

• Ben-Bassat, Oren (2012). "Gerbes and the holomorphic Brauer group of complex tori". Journal of Noncommutative Geometry. 6 (3): 407–455. arXiv:0811.2746. doi:10.4171/JNCG/96. S2CID 15049025. - Extends idea of using alternating forms on the lattice to ${\text{Alt}}^{3}(\Lambda ,\mathbb {Z} )$, to construct gerbes on a complex torus
• Block, Jonathan; Daenzer, Calder (2008). "Mukai duality for gerbes with connection". Crelle's Journal. arXiv:0803.1529v2. - includes examples of gerbes on complex tori
• Ben-Bassat, Oren (2013). "Equivariant gerbes on complex tori". Journal of Geometry and Physics. 64: 209–221. arXiv:1102.2312. Bibcode:2013JGP....64..209B. doi:10.1016/j.geomphys.2012.10.012. S2CID 119599648.
• Felder, Giovanni; Henriques, André; Rossi, Carlo A.; Zhu, Chenchang (2008). "A gerbe for the elliptic gamma function". Duke Mathematical Journal. 141. arXiv:math/0601337. doi:10.1215/S0012-7094-08-14111-0. S2CID 817920. - could be extended to complex tori

P-adic tori

• p-adic Abelian Integrals: from Theory to Practice