This article is currently being merged. After a discussion, consensus to merge this article with Range of a projectile was found. You can help implement the merge by following the instructions at Help:Merging and the resolution on the discussion. |
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|
Projectile motion is a form of motion experienced by an object or particle (a projectile) that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object's inertia, no external force is needed to maintain the horizontal velocity component of the object's motion. Taking other forces into account, such as aerodynamic drag or internal propulsion (such as in a rocket), requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.


Ballistics (from Ancient Greek βάλλειν bállein 'to throw') is the science of dynamics that deals with the flight, behavior and effects of projectiles, especially bullets, unguided bombs, rockets, or the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance.

The elementary equation of ballistics neglect nearly every factor except for initial velocity and an assumed constant gravitational acceleration. Practical solutions of a ballistics problem often require considerations of air resistance, cross winds, target motion, varying acceleration due to gravity, and in such problems as launching a rocket from one point on the Earth to another, the rotation of the Earth. Detailed mathematical solutions of practical problems typically do not have closed-form solutions, and therefore require numerical methods to address.
Kinematic quantities edit
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other. This is the principle of compound motion established by Galileo in 1638,[1] and used by him to prove the parabolic form of projectile motion.[2]
A ballistic trajectory is a parabola with homogeneous acceleration, such as in a space ship with constant acceleration in absence of other forces. On Earth the acceleration changes magnitude with altitude and direction with latitude/longitude. This causes an elliptic trajectory, which is very close to a parabola on a small scale. However, if an object was thrown and the Earth was suddenly replaced with a black hole of equal mass, it would become obvious that the ballistic trajectory is part of an elliptic orbit around that black hole, and not a parabola that extends to infinity. At higher speeds the trajectory can also be circular, parabolic or hyperbolic (unless distorted by other objects like the Moon or the Sun). In this article a homogeneous acceleration is assumed.
Acceleration edit
Since there is acceleration only in the vertical direction, the velocity in the horizontal direction is constant, being equal to . The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, being equal to g.[note 1] The components of the acceleration are:
- ,
- .*
*The y acceleration can also be referred to as the force of the earth on the object(s) of interest.
Velocity edit
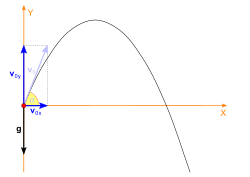
Let the projectile be launched with an initial velocity , which can be expressed as the sum of horizontal and vertical components as follows:
- .
The components and can be found if the initial launch angle, , is known:
- ,
The horizontal component of the velocity of the object remains unchanged throughout the motion. The vertical component of the velocity changes linearly,[note 2] because the acceleration due to gravity is constant. The accelerations in the x and y directions can be integrated to solve for the components of velocity at any time t, as follows:
- ,
- .
The magnitude of the velocity (under the Pythagorean theorem, also known as the triangle law):
- .
Displacement edit
At any time , the projectile's horizontal and vertical displacement are:
- ,
- .
The magnitude of the displacement is:
- .
Consider the equations,
- .[3]
If t is eliminated between these two equations the following equation is obtained:
Here R is the Range of a projectile.
Since g, θ, and v0 are constants, the above equation is of the form
- ,
in which a and b are constants. This is the equation of a parabola, so the path is parabolic. The axis of the parabola is vertical.
If the projectile's position (x,y) and launch angle (θ or α) are known, the initial velocity can be found solving for v0 in the aforementioned parabolic equation:
- .
Displacement in polar coordinates edit
The parabolic trajectory of a projectile can also be expressed in polar coordinates instead of Cartesian coordinates. In this case, the position has the general formula
- .
In this equation, the origin is the midpoint of the horizontal range of the projectile, and if the ground is flat, the parabolic arc is plotted in the range . This expression can be obtained by transforming the Cartesian equation as stated above by and .
Properties of the trajectory edit
Time of flight or total time of the whole journey edit
The total time t for which the projectile remains in the air is called the time of flight.
After the flight, the projectile returns to the horizontal axis (x-axis), so .
Note that we have neglected air resistance on the projectile.
If the starting point is at height y0 with respect to the point of impact, the time of flight is:
As above, this expression can be reduced to
if θ is 45° and y0 is 0.
Time of flight to the target's position edit
As shown above in the Displacement section, the horizontal and vertical velocity of a projectile are independent of each other.
Because of this, we can find the time to reach a target using the displacement formula for the horizontal velocity:
This equation will give the total time t the projectile must travel for to reach the target's horizontal displacement, neglecting air resistance.
Maximum height of projectile edit
The greatest height that the object will reach is known as the peak of the object's motion. The increase in height will last until , that is,
- .
Time to reach the maximum height(h):
- .
For the vertical displacement of the maximum height of the projectile:
The maximum reachable height is obtained for θ=90°:
If the projectile's position (x,y) and launch angle (θ) are known, the maximum height can be found by solving for h in the following equation:
Angle of elevation (φ) at the maximum height is given by:
Relation between horizontal range and maximum height edit
The relation between the range d on the horizontal plane and the maximum height h reached at is:
Proof
|
|---|
|
. If |
Maximum distance of projectile edit
The range and the maximum height of the projectile does not depend upon its mass. Hence range and maximum height are equal for all bodies that are thrown with the same velocity and direction. The horizontal range d of the projectile is the horizontal distance it has traveled when it returns to its initial height ( ).
- .
Time to reach ground:
- .
From the horizontal displacement the maximum distance of projectile:
- ,
so[note 3]
- .
Note that d has its maximum value when
- ,
which necessarily corresponds to
- ,
or
- .
The total horizontal distance (d) traveled.
When the surface is flat (initial height of the object is zero), the distance traveled:[4]
Thus the maximum distance is obtained if θ is 45 degrees. This distance is:
Application of the work energy theorem edit
According to the work-energy theorem the vertical component of velocity is:
- .
These formulae ignore aerodynamic drag and also assume that the landing area is at uniform height 0.
Angle of reach edit
The "angle of reach" is the angle (θ) at which a projectile must be launched in order to go a distance d, given the initial velocity v.
There are two solutions:
- (shallow trajectory)
and because ,
- (steep trajectory)
Angle θ required to hit coordinate (x, y) edit
To hit a target at range x and altitude y when fired from (0,0) and with initial speed v the required angle(s) of launch θ are:
The two roots of the equation correspond to the two possible launch angles, so long as they aren't imaginary, in which case the initial speed is not great enough to reach the point (x,y) selected. This formula allows one to find the angle of launch needed without the restriction of .
One can also ask what launch angle allows the lowest possible launch velocity. This occurs when the two solutions above are equal, implying that the quantity under the square root sign is zero. This requires solving a quadratic equation for , and we find
This gives
If we denote the angle whose tangent is y/x by α, then
This implies
In other words, the launch should be at the angle halfway between the target and Zenith (vector opposite to Gravity)
Total Path Length of the Trajectory edit
The length of the parabolic arc traced by a projectile L, given that the height of launch and landing is the same and that there is no air resistance, is given by the formula:
where is the initial velocity, is the launch angle and is the acceleration due to gravity as a positive value. The expression can be obtained by evaluating the arc length integral for the height-distance parabola between the bounds initial and final displacements (i.e. between 0 and the horizontal range of the projectile) such that:
If the time of flight is t,
Trajectory of a projectile with air resistance edit
without drag
with Stokes' drag
with Newtonian drag
Air resistance creates a force that (for symmetric projectiles) is always directed against the direction of motion in the surrounding medium and has a magnitude that depends on the absolute speed: . The speed-dependence of the friction force is linear ( ) at very low speeds (Stokes drag) and quadratic ( ) at larger speeds (Newton drag).[5] The transition between these behaviours is determined by the Reynolds number, which depends on speed, object size and kinematic viscosity of the medium. For Reynolds numbers below about 1000, the dependence is linear, above it becomes quadratic. In air, which has a kinematic viscosity around , this means that the drag force becomes quadratic in v when the product of speed and diameter is more than about , which is typically the case for projectiles.
- Stokes drag: (for )
- Newton drag: (for )
The free body diagram on the right is for a projectile that experiences air resistance and the effects of gravity. Here, air resistance is assumed to be in the direction opposite of the projectile's velocity:
Trajectory of a projectile with Stokes drag edit
Stokes drag, where , only applies at very low speed in air, and is thus not the typical case for projectiles. However, the linear dependence of on causes a very simple differential equation of motion
in which the two cartesian components become completely independent, and thus easier to solve.[6] Here, , and will be used to denote the initial velocity, the velocity along the direction of x and the velocity along the direction of y, respectively. The mass of the projectile will be denoted by m, and . For the derivation only the case where is considered. Again, the projectile is fired from the origin (0,0).
Derivation of horizontal position
|
|---|
|
The relationships that represent the motion of the particle are derived by Newton's Second Law, both in the x and y directions. In the x direction and in the y direction . This implies that: (1), and (2) Solving (1) is an elementary differential equation, thus the steps leading to a unique solution for vx and, subsequently, x will not be enumerated. Given the initial conditions (where vx0 is understood to be the x component of the initial velocity) and for : (1a) |
- (1b)
Derivation of vertical position
|
|---|
|
While (1) is solved much in the same way, (2) is of distinct interest because of its non-homogeneous nature. Hence, we will be extensively solving (2). Note that in this case the initial conditions are used and when . (2) (2a) This first order, linear, non-homogeneous differential equation may be solved a number of ways; however, in this instance, it will be quicker to approach the solution via an integrating factor . (2c) (2d) (2e) (2f) (2g)
(3) Solving for our initial conditions: (2h) (3a) |
- (3b)
Derivation of the time of flight
|
|---|
|
The total time of the journey in the presence of air resistance (more specifically, when ) can be calculated by the same strategy as above, namely, we solve the equation . While in the case of zero air resistance this equation can be solved elementarily, here we shall need the Lambert W function. The equation is of the form , and such an equation can be transformed into an equation solvable by the function (see an example of such a transformation here). Some algebra shows that the total time of flight, in closed form, is given as[7] |
- .
Trajectory of a projectile with Newton drag edit
The most typical case of air resistance, for the case of Reynolds numbers above about 1000 is Newton drag with a drag force proportional to the speed squared, . In air, which has a kinematic viscosity around , this means that the product of speed and diameter must be more than about .
Unfortunately, the equations of motion can not be easily solved analytically for this case. Therefore, a numerical solution will be examined.
The following assumptions are made:
- Constant gravitational acceleration
- Air resistance is given by the following drag formula,
- Where:
- FD is the drag force
- c is the drag coefficient
- ρ is the air density
- A is the cross sectional area of the projectile
- μ = k/m = cρA/(2m)
Special cases edit
Even though the general case of a projectile with Newton drag cannot be solved analytically, some special cases can. Here we denote the terminal velocity in free-fall as and the characteristic settling time constant .
- Near-horizontal motion: In case the motion is almost horizontal, , such as a flying bullet, the vertical velocity component has very little influence on the horizontal motion. In this case:[8]
- The same pattern applies for motion with friction along a line in any direction, when gravity is negligible. It also applies when vertical motion is prevented, such as for a moving car with its engine off.
- Vertical motion upward:[8]
- Here
- and
- where is the initial upward velocity at and the initial position is .
- A projectile cannot rise longer than in the vertical direction before it reaches the peak.
- Vertical motion downward:[8]
- After a time , the projectile reaches almost terminal velocity .
Numerical solution edit
A projectile motion with drag can be computed generically by numerical integration of the ordinary differential equation, for instance by applying a reduction to a first-order system. The equation to be solved is
- .
This approach also allows to add the effects of speed-dependent drag coefficient, altitude-dependent air density and position-dependent gravity field.
Lofted trajectory edit
A special case of a ballistic trajectory for a rocket is a lofted trajectory, a trajectory with an apogee greater than the minimum-energy trajectory to the same range. In other words, the rocket travels higher and by doing so it uses more energy to get to the same landing point. This may be done for various reasons such as increasing distance to the horizon to give greater viewing/communication range or for changing the angle with which a missile will impact on landing. Lofted trajectories are sometimes used in both missile rocketry and in spaceflight.[9]
Projectile motion on a planetary scale edit
When a projectile without air resistance travels a range that is significant compared to the Earth's radius (above ≈100 km), the curvature of the Earth and the non-uniform Earth's gravity have to be considered. This is for example the case with spacecraft or intercontinental projectiles. The trajectory then generalizes from a parabola to a Kepler-ellipse with one focus at the center of the Earth. The projectile motion then follows Kepler's laws of planetary motion.
The trajectories' parameters have to be adapted from the values of a uniform gravity field stated above. The Earth radius is taken as R, and g as the standard surface gravity. Let the launch velocity relative to the first cosmic velocity.
Total range d between launch and impact:
Maximum range of a projectile for optimum launch angle ( ):
- with , the first cosmic velocity
Maximum height of a projectile above the planetary surface:
Maximum height of a projectile for vertical launch ( ):
- with , the second cosmic velocity
Time of flight:
See also edit
Notes edit
- ^ g is the acceleration due to gravity. ( near the surface of the Earth).
- ^ decreasing when the object goes upward, and increasing when it goes downward
- ^
References edit
- ^ Galileo Galilei, Two New Sciences, Leiden, 1638, p.249
- ^ Nolte, David D., Galileo Unbound (Oxford University Press, 2018) pp. 39-63.
- ^ Stewart, James; Clegg, Dan; Watson, Saleem (2021). Calculus: Early Transcendentals (Ninth ed.). Boston, MA: Cengage. p. 919. ISBN 978-1-337-61392-7.
- ^ Tatum (2019). Classical Mechanics (PDF). pp. ch. 7.
- ^ Stephen T. Thornton; Jerry B. Marion (2007). Classical Dynamics of Particles and Systems. Brooks/Cole. p. 59. ISBN 978-0-495-55610-7.
- ^ Atam P. Arya; Atam Parkash Arya (September 1997). Introduction to Classical Mechanics. Prentice Hall Internat. p. 227. ISBN 978-0-13-906686-3.
- ^ Rginald Cristian, Bernardo; Jose Perico, Esguerra; Jazmine Day, Vallejos; Jeff Jerard, Canda (2015). "Wind-influenced projectile motion". European Journal of Physics. 36 (2): 025016. Bibcode:2015EJPh...36b5016B. doi:10.1088/0143-0807/36/2/025016. S2CID 119601402.
- ^ a b c Walter Greiner (2004). Classical Mechanics: Point Particles and Relativity. Springer Science & Business Media. p. 181. ISBN 0-387-95586-0.
- ^ Ballistic Missile Defense, Glossary, v. 3.0, US Department of Defense, June 1997.