Spring_resonance.gif (338 × 343 pixels, file size: 308 KB, MIME type: image/gif, looped, 100 frames, 5.0 s)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
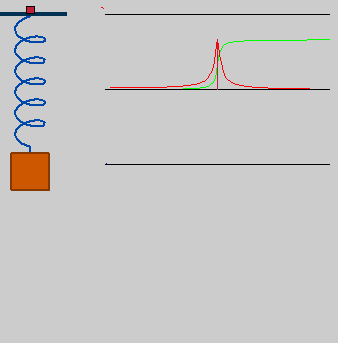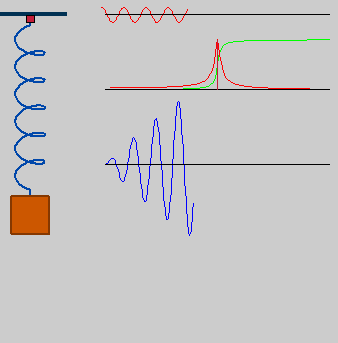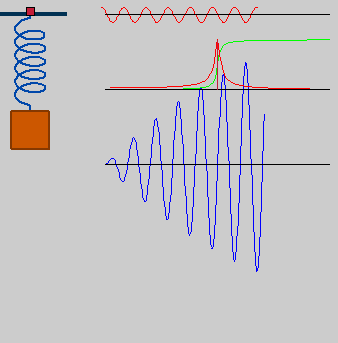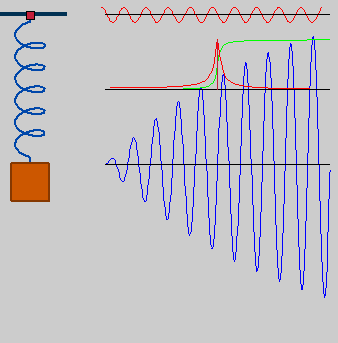
| DescriptionSpring resonance.gif |
Deutsch: getriebener Oszillator in Resonanz, omega_drive=omega0*1 |
| Date | |
| Source | Own work |
| Author | Jkrieger |
base upon work by Oleg Alexandrov: [Simple harmonic oscillator.gif]
This diagram was created with MATLAB.
Source code
function main()
% colors
red = [0.867 0.06 0.14];
blue = [0 129 205]/256;
green = [0 200 70]/256;
black = [0 0 0];
white = [1 1 1]*0.99;
cardinal = [196 30 58]/256;
cerulean = [0 123 167]/256;
denim = [21 96 189]/256;
cobalt = [0 71 171]/256;
pblue = [0 49 83]/256;
teracotta= [226 114 91]/256;
tene = [205 87 0]/256;
wall_color = pblue;
spring_color = cobalt;
mass_color = tene;
exc_color=cardinal;
a=0.65; bmass_color = a*mass_color+(1-a)*black;
% linewidth and fontsize
lw=2;
fs=20;
ww = 0.5; % wall width
ms = 0.25; % the size of the mass
sw=0.1; % spring width
curls = 5;
exc_size=0.05;
plot_width=1.5; % width of plots
K_osz = 0.05; % excitation amplitude
omega =1; % excitation frequency
omega0=1; % eigen frequency
gamma=0.02; % damping factor
filename='spring_resonance.gif';
frames=100;
options = odeset('RelTol',1e-4,'AbsTol',1e-4);
[T,YODE] = ode45(@(t,y) dampedoszi(t,y,K_osz, omega, omega0, gamma),[0 20*pi],[0 0],options);
figure(2)
plot(T,YODE(:,1));
A = 0.2; % the amplitude of spring oscillations
B = -1; % the y coordinate of the base state (the origin is higher, at the wall)
% Each of the small lines has length l
l = 0.05;
N = length(T); % times per oscillation
No = 1; % number of oscillations
for f = 1:frames
i=floor(length(T)/frames*f);
% set up the plotting window
figure(1); clf; hold on; axis equal; axis off;
t = T(i); % current time
POSW=K_osz*sin(omega*t); % position of exciter with cos-excitation is a sine!
H= B+YODE(i); % position of the mass
%H=K/sqrt((1-omega).^2+(2*gamma*omega).^2)*cos(
% plot the spring from Start to End
Start = [0, POSW]; End = [0, POSW+H];
[X, Y]=do_plot_spring(Start, End, curls, sw);
plot(X, Y, 'linewidth', lw, 'color', spring_color);
% Here we cheat. We modify the point B so that the mass is attached exactly at the end of the
% spring. This should not be necessary. I am too lazy to to the exact calculation.
K = length(X); End(1) = X(K); End(2) = Y(K);
% plot the wall from which the spring is hanging
plot_wall(-ww/2, ww/2, l, lw, wall_color);
% plot the mass at the end of the spring
X=[-ms/2 ms/2 ms/2 -ms/2 -ms/2 ms/2]+End(1); Y=[0 0 -ms -ms 0 0]+End(2);
H=fill(X, Y, mass_color, 'EdgeColor', bmass_color, 'linewidth', lw);
% plot exciter
rectangle('Position',[0-exc_size/2,POSW-exc_size/2,exc_size,exc_size], 'FaceColor',exc_color)
% the bounding box
Sx = -0.4*ww; Sy = B-max(abs(YODE(:,1)))-ms-0.05;
Lx = ww+l+plot_width; Ly=l+K_osz;
axis([Sx, Lx, Sy, Ly]);
% plot amplitude time course
plot(ww+T(1:i)./max(T).*plot_width, B+YODE(1:i,1), 'b-');
line([ww ww+plot_width], [B B], 'Color', black);
plot(ww+(T(1:i)-1)./(max(T)+1).*plot_width, K_osz*cos(omega*T(1:i)), 'r-');
line([ww ww+plot_width], [0 0], 'Color', black);
% plot resonance curve
omeg=0.05:0.01:2;
phase=atan2(-2.*gamma.*omeg, (omega0.^2-omeg.^2));
amplitude=K./sqrt((omega0^2-omeg.^2).^2+(2*gamma*omeg).^2);
plot(ww+omeg./max(omeg).*plot_width, B/2+B/3*phase/abs(max(phase)-min(phase)), 'g-')
plot(ww+omeg./max(omeg).*plot_width, B/2-B/3*amplitude/abs(max(amplitude)-min(amplitude)), 'r-')
line([ww ww+plot_width], [B/2 B/2], 'Color', black);
rx=ww+omega/max(omeg).*plot_width;
line([rx rx], [B/2 B/2-B/3], 'Color', cardinal)
frame=getframe;
[im,map1] = rgb2ind(frame.cdata,32,'nodither');
if f==1
map=map1;
imwrite(im, map, filename, 'gif', 'WriteMode', 'overwrite', 'DelayTime', 0.05, 'LoopCount', Inf);
else
im= rgb2ind(frame.cdata,map);
imwrite(im, map, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.05);
end
disp(sprintf('Spring_frame%d', 1000+f)); %show the frame number we are at
pause(0.1);
end
function dy = dampedoszi(t,y, K, omega, omega0, gamma);
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = K*cos(omega*t)-2*gamma*y(2)-omega0^2*y(1);
function dy = damper(t,y, K, omega, omega0, gamma);
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = K*cos(omega*t);
function [X, Y]=do_plot_spring(A, B, curls, sw);
% plot a 3D spring, then project it onto 2D. theta controls the angle of projection.
% The string starts at A and ends at B
% will rotate by theta when projecting from 1D to 2D
theta=pi/6;
Npoints = 500;
% spring length
D = sqrt((A(1)-B(1))^2+(A(2)-B(2))^2);
X=linspace(0, 1, Npoints);
XX = linspace(-pi/2, 2*pi*curls+pi/2, Npoints);
Y=-sw*cos(XX);
Z=sw*sin(XX);
% b gives the length of the small straight segments at the ends
% of the spring (to which the wall and the mass are attached)
b= 0.05;
% stretch the spring in X to make it of length D - 2*b
N = length(X);
X = (D-2*b)*(X-X(1))/(X(N)-X(1));
% shift by b to the right and add the two small segments of length b
X=[0, X+b X(N)+2*b]; Y=[Y(1) Y Y(N)]; Z=[Z(1) Z Z(N)];
% project the 3D spring to 2D
M=[cos(theta) sin(theta); -sin(theta) cos(theta)];
N=length(X);
for i=1:N;
V=M*[X(i), Z(i)]';
X(i)=V(1); Z(i)=V(2);
end
% shift the spring to start from 0
X = X-X(1);
% now that we have the horisontal spring (X, Y) of length D,
% rotate and translate it to go from A to B
Theta = atan2(B(2)-A(2), B(1)-A(1));
M=[cos(Theta) -sin(Theta); sin(Theta) cos(Theta)];
N=length(X);
for i=1:N;
V=M*[X(i), Y(i)]'+A';
X(i)=V(1); Y(i)=V(2);
end
function plot_wall(S, E, l, lw, wall_color)
% Plot a wall from S to E.
no=20; spacing=(E-S)/(no-1);
plot([S, E], [0, 0], 'linewidth', 1.8*lw, 'color', wall_color);
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
29 January 2012
image/gif
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:19, 29 January 2012 |  | 338 × 343 (308 KB) | Jkrieger |
File usage
No pages on the English Wikipedia use this file (pages on other projects are not listed).
Global file usage
The following other wikis use this file:
- Usage on ca.wikipedia.org
- Usage on de.wikipedia.org
- Usage on pt.wikipedia.org
- Usage on ta.wikipedia.org
Retrieved from "https://en.wikipedia.org/wiki/File:Spring_resonance.gif"