
Size of this preview: 728 × 600 pixels. Other resolutions: 292 × 240 pixels | 583 × 480 pixels | 933 × 768 pixels | 1,244 × 1,024 pixels | 1,700 × 1,400 pixels.
Original file (1,700 × 1,400 pixels, file size: 534 KB, MIME type: image/png)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 14:36, 22 April 2007 | 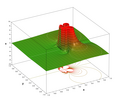 | 1,700 × 1,400 (534 KB) | Inductiveload | {{Information |Description=Diagram of the absolute value of the imaginary part of exponential function in the complex plane, as the operand approaches infinity. The plot is given by: ::<math>z=\bigg|\operatorname{Im} \left (\exp \left( \frac{1}{x + i y} \ |
File usage
No pages on the English Wikipedia use this file (pages on other projects are not listed).
Global file usage
The following other wikis use this file:
- Usage on et.wikipedia.org
