A restricted Boltzmann machine (RBM) (also called a restricted Sherrington–Kirkpatrick model with external field or restricted stochastic Ising–Lenz–Little model) is a generative stochastic artificial neural network that can learn a probability distribution over its set of inputs.[1]
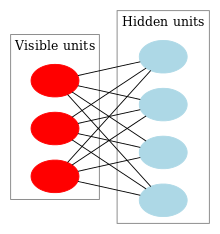
RBMs were initially proposed under the name Harmonium by Paul Smolensky in 1986,[2] and rose to prominence after Geoffrey Hinton and collaborators used fast learning algorithms for them in the mid-2000s. RBMs have found applications in dimensionality reduction,[3] classification,[4] collaborative filtering,[5] feature learning,[6] topic modelling,[7] immunology,[8] and even many‑body quantum mechanics.[9] [10] [11]
They can be trained in either supervised or unsupervised ways, depending on the task.[citation needed]
As their name implies, RBMs are a variant of Boltzmann machines, with the restriction that their neurons must form a bipartite graph:
- a pair of nodes from each of the two groups of units (commonly referred to as the "visible" and "hidden" units respectively) may have a symmetric connection between them; and
- there are no connections between nodes within a group.
By contrast, "unrestricted" Boltzmann machines may have connections between hidden units. This restriction allows for more efficient training algorithms than are available for the general class of Boltzmann machines, in particular the gradient-based contrastive divergence algorithm.[12]
Restricted Boltzmann machines can also be used in deep learning networks. In particular, deep belief networks can be formed by "stacking" RBMs and optionally fine-tuning the resulting deep network with gradient descent and backpropagation.[13]
Structure
editThe standard type of RBM has binary-valued (Boolean) hidden and visible units, and consists of a matrix of weights of size . Each weight element of the matrix is associated with the connection between the visible (input) unit and the hidden unit . In addition, there are bias weights (offsets) for and for . Given the weights and biases, the energy of a configuration (pair of Boolean vectors) (v,h) is defined as
or, in matrix notation,
This energy function is analogous to that of a Hopfield network. As with general Boltzmann machines, the joint probability distribution for the visible and hidden vectors is defined in terms of the energy function as follows,[14]
where is a partition function defined as the sum of over all possible configurations, which can be interpreted as a normalizing constant to ensure that the probabilities sum to 1. The marginal probability of a visible vector is the sum of over all possible hidden layer configurations,[14]
- ,
and vice versa. Since the underlying graph structure of the RBM is bipartite (meaning there are no intra-layer connections), the hidden unit activations are mutually independent given the visible unit activations. Conversely, the visible unit activations are mutually independent given the hidden unit activations.[12] That is, for m visible units and n hidden units, the conditional probability of a configuration of the visible units v, given a configuration of the hidden units h, is
- .
Conversely, the conditional probability of h given v is
- .
The individual activation probabilities are given by
- and
where denotes the logistic sigmoid.
The visible units of Restricted Boltzmann Machine can be multinomial, although the hidden units are Bernoulli.[clarification needed] In this case, the logistic function for visible units is replaced by the softmax function
where K is the number of discrete values that the visible values have. They are applied in topic modeling,[7] and recommender systems.[5]
Relation to other models
editRestricted Boltzmann machines are a special case of Boltzmann machines and Markov random fields.[15][16]
The graphical model of RBMs corresponds to that of factor analysis.[17]
Training algorithm
edit
Restricted Boltzmann machines are trained to maximize the product of probabilities assigned to some training set (a matrix, each row of which is treated as a visible vector ),
or equivalently, to maximize the expected log probability of a training sample selected randomly from :[15][16]
The algorithm most often used to train RBMs, that is, to optimize the weight matrix , is the contrastive divergence (CD) algorithm due to Hinton, originally developed to train PoE (product of experts) models.[18][19] The algorithm performs Gibbs sampling and is used inside a gradient descent procedure (similar to the way backpropagation is used inside such a procedure when training feedforward neural nets) to compute weight update.
The basic, single-step contrastive divergence (CD-1) procedure for a single sample can be summarized as follows:
- Take a training sample v, compute the probabilities of the hidden units and sample a hidden activation vector h from this probability distribution.
- Compute the outer product of v and h and call this the positive gradient.
- From h, sample a reconstruction v' of the visible units, then resample the hidden activations h' from this. (Gibbs sampling step)
- Compute the outer product of v' and h' and call this the negative gradient.
- Let the update to the weight matrix be the positive gradient minus the negative gradient, times some learning rate: .
- Update the biases a and b analogously: , .
A Practical Guide to Training RBMs written by Hinton can be found on his homepage.[14]
Stacked Restricted Boltzmann Machine
editThis section may be too technical for most readers to understand. (August 2023) |
This section needs additional citations for verification. (August 2023) |
- The difference between the Stacked Restricted Boltzmann Machines and RBM is that RBM has lateral connections within a layer that are prohibited to make analysis tractable. On the other hand, the Stacked Boltzmann consists of a combination of an unsupervised three-layer network with symmetric weights and a supervised fine-tuned top layer for recognizing three classes.
- The usage of Stacked Boltzmann is to understand Natural languages, retrieve documents, image generation, and classification. These functions are trained with unsupervised pre-training and/or supervised fine-tuning. Unlike the undirected symmetric top layer, with a two-way unsymmetric layer for connection for RBM. The restricted Boltzmann's connection is three-layers with asymmetric weights, and two networks are combined into one.
- Stacked Boltzmann does share similarities with RBM, the neuron for Stacked Boltzmann is a stochastic binary Hopfield neuron, which is the same as the Restricted Boltzmann Machine. The energy from both Restricted Boltzmann and RBM is given by Gibb's probability measure: . The training process of Restricted Boltzmann is similar to RBM. Restricted Boltzmann train one layer at a time and approximate equilibrium state with a 3-segment pass, not performing back propagation. Restricted Boltzmann uses both supervised and unsupervised on different RBM for pre-training for classification and recognition. The training uses contrastive divergence with Gibbs sampling: Δwij = e*(pij - p'ij)
- The restricted Boltzmann's strength is it performs a non-linear transformation so it's easy to expand, and can give a hierarchical layer of features. The Weakness is that it has complicated calculations of integer and real-valued neurons. It does not follow the gradient of any function, so the approximation of Contrastive divergence to maximum likelihood is improvised.[14]
Literature
edit- Fischer, Asja; Igel, Christian (2012), "An Introduction to Restricted Boltzmann Machines", Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, Lecture Notes in Computer Science, vol. 7441, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 14–36, doi:10.1007/978-3-642-33275-3_2, ISBN 978-3-642-33274-6
See also
editReferences
edit- ^ Sherrington, David; Kirkpatrick, Scott (1975), "Solvable Model of a Spin-Glass", Physical Review Letters, 35 (35): 1792–1796, Bibcode:1975PhRvL..35.1792S, doi:10.1103/PhysRevLett.35.1792
- ^ Smolensky, Paul (1986). "Chapter 6: Information Processing in Dynamical Systems: Foundations of Harmony Theory" (PDF). In Rumelhart, David E.; McLelland, James L. (eds.). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations. MIT Press. pp. 194–281. ISBN 0-262-68053-X.
- ^ Hinton, G. E.; Salakhutdinov, R. R. (2006). "Reducing the Dimensionality of Data with Neural Networks" (PDF). Science. 313 (5786): 504–507. Bibcode:2006Sci...313..504H. doi:10.1126/science.1127647. PMID 16873662. S2CID 1658773. Archived from the original (PDF) on 2015-12-23. Retrieved 2015-12-02.
- ^ Larochelle, H.; Bengio, Y. (2008). Classification using discriminative restricted Boltzmann machines (PDF). Proceedings of the 25th international conference on Machine learning - ICML '08. p. 536. doi:10.1145/1390156.1390224. ISBN 978-1-60558-205-4.
- ^ a b Salakhutdinov, R.; Mnih, A.; Hinton, G. (2007). Restricted Boltzmann machines for collaborative filtering. Proceedings of the 24th international conference on Machine learning - ICML '07. p. 791. doi:10.1145/1273496.1273596. ISBN 978-1-59593-793-3.
- ^ Coates, Adam; Lee, Honglak; Ng, Andrew Y. (2011). An analysis of single-layer networks in unsupervised feature learning (PDF). International Conference on Artificial Intelligence and Statistics (AISTATS). Archived from the original (PDF) on 2014-12-20. Retrieved 2014-12-19.
- ^ a b Ruslan Salakhutdinov and Geoffrey Hinton (2010). Replicated softmax: an undirected topic model Archived 2012-05-25 at the Wayback Machine. Neural Information Processing Systems 23.
- ^ Bravi, Barbara; Di Gioacchino, Andrea; Fernandez-de-Cossio-Diaz, Jorge; Walczak, Aleksandra M; Mora, Thierry; Cocco, Simona; Monasson, Rémi (2023-09-08). Bitbol, Anne-Florence; Eisen, Michael B (eds.). "A transfer-learning approach to predict antigen immunogenicity and T-cell receptor specificity". eLife. 12: e85126. doi:10.7554/eLife.85126. ISSN 2050-084X. PMC 10522340. PMID 37681658.
- ^ Carleo, Giuseppe; Troyer, Matthias (2017-02-10). "Solving the quantum many-body problem with artificial neural networks". Science. 355 (6325): 602–606. arXiv:1606.02318. Bibcode:2017Sci...355..602C. doi:10.1126/science.aag2302. ISSN 0036-8075. PMID 28183973. S2CID 206651104.
- ^ Melko, Roger G.; Carleo, Giuseppe; Carrasquilla, Juan; Cirac, J. Ignacio (September 2019). "Restricted Boltzmann machines in quantum physics". Nature Physics. 15 (9): 887–892. Bibcode:2019NatPh..15..887M. doi:10.1038/s41567-019-0545-1. ISSN 1745-2481. S2CID 256704838.
- ^ Pan, Ruizhi; Clark, Charles W. (2024). "Efficiency of neural-network state representations of one-dimensional quantum spin systems". Physical Review Research. 6: 023193. arXiv:2302.00173. doi:10.1103/PhysRevResearch.6.023193.
- ^ a b Miguel Á. Carreira-Perpiñán and Geoffrey Hinton (2005). On contrastive divergence learning. Artificial Intelligence and Statistics.
- ^ Hinton, G. (2009). "Deep belief networks". Scholarpedia. 4 (5): 5947. Bibcode:2009SchpJ...4.5947H. doi:10.4249/scholarpedia.5947.
- ^ a b c d Geoffrey Hinton (2010). A Practical Guide to Training Restricted Boltzmann Machines. UTML TR 2010–003, University of Toronto.
- ^ a b Sutskever, Ilya; Tieleman, Tijmen (2010). "On the convergence properties of contrastive divergence" (PDF). Proc. 13th Int'l Conf. On AI and Statistics (AISTATS). Archived from the original (PDF) on 2015-06-10.
- ^ a b Asja Fischer and Christian Igel. Training Restricted Boltzmann Machines: An Introduction Archived 2015-06-10 at the Wayback Machine. Pattern Recognition 47, pp. 25-39, 2014
- ^ María Angélica Cueto; Jason Morton; Bernd Sturmfels (2010). "Geometry of the restricted Boltzmann machine". Algebraic Methods in Statistics and Probability. 516. American Mathematical Society. arXiv:0908.4425. Bibcode:2009arXiv0908.4425A.
- ^ Geoffrey Hinton (1999). Products of Experts. ICANN 1999.
- ^ Hinton, G. E. (2002). "Training Products of Experts by Minimizing Contrastive Divergence" (PDF). Neural Computation. 14 (8): 1771–1800. doi:10.1162/089976602760128018. PMID 12180402. S2CID 207596505.
Bibliography
edit- Chen, Edwin (2011-07-18). "Introduction to Restricted Boltzmann Machines". Edwin Chen's blog.
- Nicholson, Chris; Gibson, Adam. "A Beginner's Tutorial for Restricted Boltzmann Machines". Deeplearning4j Documentation. Archived from the original on 2017-02-11. Retrieved 2018-11-15.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - Nicholson, Chris; Gibson, Adam. "Understanding RBMs". Deeplearning4j Documentation. Archived from the original on 2016-09-20. Retrieved 2014-12-29.
External links
edit- Python implementation of Bernoulli RBM and tutorial
- SimpleRBM is a very small RBM code (24kB) useful for you to learn about how RBMs learn and work.
- Julia implementation of Restricted Boltzmann machines: https://github.com/cossio/RestrictedBoltzmannMachines.jl