User:Thepigdog/Lambda Calculus (old)

The lowercase lambda, the 11th letter of the Greek alphabet, is used to symbolize the lambda calculus.

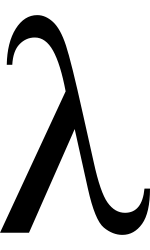
Lambda calculus (also written as λ-calculus or called "the lambda calculus") is a formal system in mathematical logic and computer science for expressing computation using variable binding and substitution. First formulated by Alonzo Church, lambda calculus found early successes in the area of computability theory, such as a negative answer to Hilbert's Entscheidungsproblem ("decision problem").

Lambda calculus is a simple yet Turing complete language, which can represent every computable function. Any program may be written in lambda calculus, and its execution can be understood knowing the definition of lambda calculus alone without reference to any external software environment or runtime library. Lambda calculus is functional, which allows a program written in the lambda calculus to be studied through mathematical methods. In particular parts of the program may be analyzed separately from other parts. The lambda calculus is not intended as a programming language for everyday use. However, it is valuable as a theoretical construct, and as a basis for understanding other languages.

Because of the importance of the notion of variable binding and substitution, there is not just one system of lambda calculus, and in particular there are typed and untyped variants. Historically, the most important system was the untyped lambda calculus, in which function application has no restrictions (so the notion of the domain of a function is not built into the system). In the Church–Turing Thesis, the untyped lambda calculus is claimed to be capable of computing all effectively calculable functions. The typed lambda calculus is a variety that restricts function application, so that functions can only be applied if they are capable of accepting the given input's "type" of data.

Today, the lambda calculus has applications in many different areas in mathematics, philosophy, linguistics, and computer science. It is still used in the area of computability theory, although Turing machines are also an important model for computation. Lambda calculus has played an important role in the development of the theory of programming languages. Counterparts to lambda calculus in computer science are functional programming languages, which essentially implement the calculus (augmented with some constants and datatypes). Beyond programming languages, the lambda calculus also has many applications in proof theory. A major example of this is the Curry–Howard correspondence, which gives a correspondence between different systems of typed lambda calculus and systems of formal logic.

Lambda calculus in history of mathematics

The lambda calculus was introduced by mathematician Alonzo Church in the 1930s as part of an investigation into the foundations of mathematics. The original system was shown to be logically inconsistent in 1935 when Stephen Kleene and J. B. Rosser developed the Kleene–Rosser paradox.

Subsequently, in 1936 Church isolated and published just the portion relevant to computation, what is now called the untyped lambda calculus. In 1940, he also introduced a computationally weaker, but logically consistent system, known as the simply typed lambda calculus.

Informal description

Motivation

Computable functions are a fundamental concept within computer science and mathematics. The λ-calculus provides a simple semantics for computation, enabling properties of computation to be studied formally. The λ-calculus incorporates two simplifications that make this semantics simple.

One first simplification is that the λ-calculus treats functions "anonymously", without giving them explicit names. That is, a function can be defined as a an expression which may called. For example, the function

$\operatorname {sqsum} (x,y)=x\times x+y\times y$

can be rewritten in anonymous form as

$(x,y)\mapsto x\times x+y\times y$

(read as “the pair of $x$ and $y$ is mapped to $x\times x+y\times y$”). Similarly,

$\operatorname {id} (x)=x$

can be rewritten in anonymous form as $x\mapsto x$, where the input is simply mapped to itself.

Currying

The second simplification is that the λ-calculus only uses functions of a single input. An ordinary function that requires two inputs, for instance the $\operatorname {sqsum}$ function, can be reworked into an equivalent function that accepts a single input, and as output returns another function, that in turn accepts a single input. For example,

$(x,y)\mapsto x\times x+y\times y$

can be reworked into

$x\mapsto (y\mapsto x\times x+y\times y)$

This method, known as currying, transforms a function that takes multiple arguments into a chain of functions each with a single argument.

Applying the $\operatorname {sqsum}$ function to the arguments (5, 2), yields:

$((x,y)\mapsto x\times x+y\times y)(5,2)$

$=5\times 5+2\times 2=29$

The curried version yields:

$((x\mapsto (y\mapsto x\times x+y\times y))(5))(2)$

$=(y\mapsto 5\times 5+y\times y)(2)$

$=5\times 5+2\times 2=29$

and thus computes the same result.

The Lambda Calculus

The lambda calculus takes these ideas and transforms them into a language based only on function parameterising and application. A lambda expression looks like,

$f=\lambda xy.x^{2}+y^{2}$

which is the equivalent of writing,

$f(x,y)=x^{2}+y^{2}$

The difference in notation makes a single representation of the function $f$ in one expression. In the same way that we say that arithmetic equations are solved for numeric values, by analogy you may consider the lambda expression to be "solved" for the function variable $f$.

Function Application

A key starting point for functional languages, and the lambda calculus, is function application. Function application is considered so important for functional programming that the notation

$k(x)$ is written as $k\ x$

So in calling the function $f$ ,defined above, we write,

$f\ 5\ 6$

which may be written, $(\lambda xy.x^{2}+y^{2})5\ 6$ giving the result, $5^{2}+6^{2}$ or $61$

You see in this example that the function $f$ may be substituted for it's function expression $\lambda xy.x^{2}+y^{2}$. This makes lambda calculus language useful for thinking about and understanding the nature of computations.

Formal Definition

Syntax Definition

Lambda expressions have a simple syntax. Lambda expressions are composed of

variables v₁, v₂, ..., v_n, ...

the abstraction symbols λ and

parentheses ( )

The set of lambda expressions, Λ, can be defined inductively:

1. If x is a variable, then x ∈ Λ
2. If x is a variable and M ∈ Λ, then (λx.M) ∈ Λ
3. If M, N ∈ Λ, then (M N) ∈ Λ

Instances of rule 2 are known as abstractions and instances of rule 3 are known as applications.

Notational conventions

To keep the notation of lambda expressions uncluttered, the following conventions are usually applied.

• Outermost parentheses are dropped: M N instead of (M N)
• Applications are left associative: M N P may be written instead of ((M N) P)
• The body of an abstraction extends as far right as possible: λx.M N means λx.(M N) and not (λx.M) N
• A sequence of abstractions is contracted: λx.λy.λz.N may be abbreviated as λxyz.N

Definition of Semantics

The execution of a lambda expression proceeds using the following reductions and transformations,

1. alpha conversion - $\operatorname {alpha-con} (a)\to \operatorname {canonym} [A,P]=\operatorname {canonym} [a[A],P]$
2. beta reduction - $\operatorname {beta-redex} [\lambda \operatorname {fp} .b\operatorname {ap} ]=b[\operatorname {fp} :=\operatorname {ap} ]$
3. eta reduction - $x\not \in \operatorname {FV} (f)\to \operatorname {eta-redex} [\lambda x.(f\ x)]=f$

where,

• canonym is a renaming of a lambda expression to give the expression standard names, based on the position of the name in the expression.
• Substitution Operator, $b[\operatorname {fp} :=\operatorname {ap} ]$ is the substitution of the name $\operatorname {fp}$ by the lambda expression $\operatorname {ap}$ in lambda expression $b$.
• Free Variable Set $\operatorname {FV} (f)$ is the set of variables that do not belong to a lambda abstraction in $f$.

Execution is performing beta reductions and eta reductions on sub expressions in the canonym of a lambda expression until the result is a lambda function (abstraction) in the normal form.

All alpha conversions of a lambda expression are considered to be equivalent.

Canonym - Canonical Names

Canonym is a function that takes a lambda expression and renames all names canonically, based on their positions in the expression. This might be implemented as,

1. $\operatorname {canonym} [L,P]=\operatorname {canonym} [L,O,P]$
2. $\operatorname {canonym} [\lambda \operatorname {fp} .b,M,P]=\lambda \operatorname {name} (P).\operatorname {canonym} [b,M[\operatorname {fp} :=P],P+N]$
3. $\operatorname {canonym} [X\ Y,x,P]=\operatorname {canonym} [X,x,P+F]\ \operatorname {canonym} [Y,x,E+S]$
4. $\operatorname {canonym} [x,M,P]=\operatorname {name} (M[x])$

Where, N is the string "N", F is the string "F", S is the string "S", + is concatenation, and "name" converts a string into a name

Map Operators

Map from one value to another if the value is in the map. O is the empty map.

1. $O[x]=x$
2. $M[x:=y][x]=y$
3. $x\neq z\to M[x:=y][z]=M[z]$

Substitution Operator

If L is a lambda expression, x is a name, and y is a lambda expression; $L[x:=y]$ means substitute x by y in L. The rules are,

1. $(\lambda \operatorname {fp} .b)[x:=y]=\lambda \operatorname {fp} .b[x:=y]$
2. $(X\ Y)[x:=y]=X[x:=y]\ Y[x:=y]$
3. $z=x\to (z)[x:=y]=y$
4. $z\neq x\to (z)[x:=y]=z$

Note that rule 1 must be modified if it is to be used on non canonically renamed lambda expressions. See Changes to the substitution operator.

Free and Bound Variable Sets

The set of free variables of a lambda expression, M, is denoted as FV(M). This is the set of variable names that have instances not bound (used) in a lambda abstraction, within the lambda expression. They are the variable names that may be bound to formal parameter variables from outside the lambda expression.

The set of bound variables of a lambda expression, M, is denoted as BV(M). This is the set of variable names that have instances bound (used) in a lambda abstraction, within the lambda expression.

The rules for the two sets are given below.

$\operatorname {FV} (M)$ - Free Variable Set	Comment	$\operatorname {BV} (M)$ - Bound Variable Set	Comment
$\operatorname {FV} (x)=\{x\}$	where x is a variable	$\operatorname {BV} (x)=\{\}$	where x is a variable
$\operatorname {FV} (\lambda x.M)=\operatorname {FV} (M)\cap \neg \{x\}$	Free variables of M excluding x	$\operatorname {BV} (\lambda x.M)=\operatorname {BV} (M)\cup \{x\}$	Bound variables of M plus x.
$\operatorname {FV} (M\ N)=\operatorname {FV} (M)\cup \operatorname {FV} (N)$	Combine the free variables from the function and the parameter	$\operatorname {BV} (M\ N)=\operatorname {BV} (M)\cup \operatorname {BV} (N)$	Combine the bound variables from the function and the parameter

Usage;

• The Free Variable Set, FV is used above in the definition of the eta-reduction.
• The Bound Variable Set, BV, is used in the rule for beta-redex of non canonical lambda expression.

Usage and Influence

Rules for general use

This section gives a general discussion for how Lambda Calculus is applied and gives rules that apply when lambda expressions are not canonically renamed. When working manually with lambda expressions it is easier to understand using the variable names that the author gave.

Free and bound variables

The lambda abstraction operator, λ, takes a formal parameter variable and a body expression. When evaluated the formal parameter variable is identified with the value of the actual parameter.

Variables in a lambda expression may either be "bound" or "free". Bound variables are variable names that are already attached to formal parameter variables in the expression.

The formal parameter variable is said to bind the variable name wherever it occurs free in the body. Variable (names) that have already been matched to formal parameter variable are said to be bound. All other variables in the expression are called free.

For example, in the following expression y is a bound variable and x is free: $\lambda y.x\ x\ y$. Also note that a variable is bound by its "nearest" lambda abstraction. In the following example the single occurrence of x in the expression is bound by the second lambda: $\lambda x.y\ (\lambda x.z\ x)$

Changes to the substitution operator

In the definition of the Substitution Operator the rule,

• $\lambda \operatorname {fp} .b)[x:=y]=\lambda \operatorname {fp} .b[x:=y]$

must be replaced with,

1. $(\lambda x.b)[x:=y]=\lambda x.b]$
2. $z\neq x\ \to (\lambda z.b)[x:=y]=\lambda z.b[x:=y]$

This is to stop bound variables with the same name being substituted. This would not have occurred in a canonically renamed lambda expression.

For example the previous rules would have wrongly translated,

$(\lambda x.x\ z)[x:=y]=(\lambda x.y\ z)$

The new rules block this substitution so that it remains as,

$(\lambda x.x\ z)[x:=y]=(\lambda x.x\ z)$

Transformation

The meaning of lambda expressions is defined by how expressions can be transformed or reduced.

There are three kinds of transformation:

• α-conversion: changing bound variables (alpha);
• β-reduction: applying functions to their arguments (beta), calling functions;
• η-conversion: which captures a notion of extensionality (eta).

We also speak of the resulting equivalences: two expressions are β-equivalent, if they can be β-converted into the same expression, and α/η-equivalence are defined similarly.

The term redex, short for reducible expression, refers to subterms that can be reduced by one of the reduction rules.

Alpha Conversion

Alpha-conversion, sometimes known as alpha-renaming, allows bound variable names to be changed. For example, alpha-conversion of $\lambda x.x$ might give $\lambda y.y$. Terms that differ only by alpha-conversion are called α-equivalent.

In an alpha conversion, names may be substituted for new names if the new name is not free in the body, as this would lead to the capture of free variables.

$(y\not \in FV(b)\land a(\lambda x.b)=\lambda y.b[x:=y])\to \operatorname {alpha-con} (a)$

Note that the substitution will not recurse into the body of lambda expressions with formal parameter $x$ because of the change to the substitution operator described above.

See example;

Alpha conversion	Lambda Expression	Canonically named	Comment
	$\lambda z.\lambda y.(z\ y)$	$\lambda \operatorname {P} .\lambda \operatorname {PN} .(\operatorname {P} \operatorname {PN} )$	Original expressions.
correctly rename y to k, (because k is not used in the body)	$\lambda z.\lambda k.(z\ k)$	$\lambda \operatorname {P} .\lambda \operatorname {PN} .(\operatorname {P} \operatorname {PN} )$	No change to canonical renamed expression.
naively rename y to z, (wrong because z free in $\lambda y.(z\ y)$)	$\lambda z.\lambda z.(z\ z)$	$\lambda \operatorname {P} .\lambda \operatorname {PN} .({\color {Red}\operatorname {PN} }\operatorname {PN} )$	$z$ is captured.

Beta reduction (capture avoiding)

Beta-reduction captures the idea of function application (also called a function call), and implements the substitution of the actual parameter expression for the formal parameter variable. Beta-reduction is defined in terms of substitution.

If no variable names are free in the actual parameter and bound in the body, beta reduction may be performed on the the lambda abstraction without canonical renaming.

$(\forall z:z\not \in FV(y)\lor z\not \in BV(b))\to \operatorname {beta-redex} [\lambda x.b\ y]=b[x:=y]$

Alpha renaming may be used on $b$ to rename names that are free in $y$ but bound in $b$, to meet the pre-condition for this transformation.

See example;

Beta Reduction	Lambda Expression	Canonically named	Comment
	$(\lambda x.\lambda y.(\lambda z.(\lambda x.z\ x)(\lambda y.z\ y))(x\ y))$	$(\lambda \operatorname {P} .\lambda \operatorname {PN} .(\lambda \operatorname {PNF} .(\lambda \operatorname {PNFNF} .\operatorname {PNF} \operatorname {PNFNF} )(\lambda \operatorname {PNFNS} .\operatorname {PNF} \operatorname {PNFNS} ))(\operatorname {P} \operatorname {PN} ))$	Original expressions.
Naive beta 1,	$(\lambda x.\lambda y.((\lambda x.(x\ y)x)(\lambda y.(x\ y)y)))$	Canonical $(\lambda \operatorname {P} .\lambda \operatorname {PN} .((\lambda \operatorname {PNF} .({\color {Blue}\operatorname {P} }\operatorname {PN} )\operatorname {PNF} )(\lambda \operatorname {PNS} .(\operatorname {P} {\color {Blue}\operatorname {PN} })\operatorname {PNS} )))$ Natural $(\lambda \operatorname {P} .\lambda \operatorname {PN} .((\lambda \operatorname {PNF} .({\color {Red}\operatorname {PNF} }\operatorname {PN} )\operatorname {PNF} )(\lambda \operatorname {PNS} .(\operatorname {P} {\color {Red}\operatorname {PNS} )}\operatorname {PNS} )))$	x (P) and y (PN) have been captured in the substitution.
Alpha rename inner, x -> a, y -> b	$(\lambda x.\lambda y.(\lambda z.(\lambda x.z\ a)(\lambda b.z\ b))(x\ y))$	$(\lambda \operatorname {P} .\lambda \operatorname {PN} .(\lambda \operatorname {PNF} .(\lambda \operatorname {PNFNF} .\operatorname {PNF} \operatorname {PNFNF} )(\lambda \operatorname {PNFNS} .\operatorname {PNF} \operatorname {PNFNS} ))(\operatorname {P} \operatorname {PN} ))$
Beta 2,	$(\lambda x.\lambda y.((\lambda a.(x\ y)a)(\lambda b.(x\ y)b)))$	Canonical $(\lambda \operatorname {P} .\lambda \operatorname {PN} .((\lambda \operatorname {PNF} .(\operatorname {P} \operatorname {PN} )\operatorname {PNF} )(\lambda \operatorname {PNS} .(\operatorname {P} \operatorname {PN} )\operatorname {PNS} )))$ Natural $(\lambda \operatorname {P} .\lambda \operatorname {PN} .((\lambda \operatorname {PNF} .(\operatorname {P} \operatorname {PN} )\operatorname {PNF} )(\lambda \operatorname {PNS} .(\operatorname {P} \operatorname {PN} )\operatorname {PNS} )))$	x and y not captured.

1. $((\lambda x.z\ x)(\lambda y.z\ y))[z:=(x\ y)]$
2. $((\lambda a.z\ a)(\lambda b.z\ b))[z:=(x\ y)]$

In this example,

1. In the beta-redex,
   1. The free variables are, $FV(x\ y)=\{x,y\}$
   2. The bound variables are, $BV((\lambda x.z\ x)(\lambda y.z\ y))=\{x,y\}$
2. The naive beta-redex changed the meaning of the expression because x and y from the actual parameter became captured when the expressions were substituted in the inner abstractions.
3. The alpha renaming removed the problem by changing the names of x and y in the inner abstraction so that they are distinct from the names of x and y in the actual parameter.
   1. The free variables are, $\operatorname {FV} (x\ y)=\{x,y\}$
   2. The bound variables are, $\operatorname {BV} ((\lambda a.z\ a)(\lambda b.z\ b))=\{a,b\}$
4. The beta-redex then proceeded with the intended meaning.

Eta reduction

Eta-conversion expresses the idea of extensionality, which in this context is that two functions are the same if and only if they give the same result for all arguments.

Eta reduction may be used without change on lambda expressions that are not canonically renamed.

$x\not \in \operatorname {FV} (f)\to \operatorname {eta-redex} [\lambda x.(fx)]=f$

The problem with using an eta-redex when f has free variables is shown in this example,

Reduction	Lambda expression	Beta-reduction
	$(\lambda x.(\lambda y.y\ x)\ x)\ a$	$\lambda a.a\ a$
Naive eta-reduction	$(\lambda y.y\ x)\ a$	$\lambda a.a\ x$

This improper use of eta-reduction changes the meaning by leaving $x$ in $\lambda y.y\ x$ unsubstituted.

Normalization

Main article: Beta normal form

The purpose of beta-reduction is to calculate a value. A value in Lambda Calculus is a function. So beta-reduction continues until the expression looks like a function abstraction.

An lambda expression that cannot be reduced further, by either beta-redex, or eta-redex is in normal form. Note that alpha-conversion may convert functions. All normal forms that can be converted into each other by alpha conversion are defined to be equal. See the main article on Beta normal form for details.

Normal Form Type	Definition.
Normal Form	No beta or eta reductions are possible.
Head Normal Form	In the form of a lambda abstraction whose body is not reducible.
Weak Head Normal Form	In the form of a lambda abstraction.

Encoding datatypes

Main articles: Church encoding and Mogensen–Scott encoding

Although the Lambda calculus expression only evaluate to functions, it is possible to interpret some functions as Boolean, or numeric values. This may be achieved because there are lambda expressions that behave like the basic types. These types are described below.

• Arithmetic in lambda calculus
• Logic and predicates
• Pairs

Using these encodings it is possible to write programs about logic or arithmetic, without using any external libraries. All may be constructed out of the machinery of lambda calculus.

Combinatory logic

Main articles: Combinatory logic and Fixed point combinator

Combinatory logic is based on (or implemented in) Lambda calculus. It was introduced by Moses Schönfinkel and Haskell Curry to implement the idea that the names of the variables are unimportant. Only the variable identity is important. Combinatory logic uses some closed lambda expressions (called combinators) to implement this idea.

The basic idea is that the combinators act like plumbing parts, that may be put together to redirect the variable value where it needs to go. Combinators are used in the study of the structure of programs.

The fixed point combinator is an interesting function that takes a function and computes the value that the function maps to the same value. This is also known as Curry's Paradoxical Combinator because it may be used to implement a form of Curry's Paradox.

Lambda Lifting

Lambda lifting may be used to extract function definitions from a lambda expression and converts a lambda expression into a functional form, with no lambda abstractions.

This demonstrates the equivalence of Lambda Calculus and equations written in a functional form. Lambda Lifting may also be considered as an alternate definition for Lambda Calculus.

Each lift may be considered as a refactoring step, in that it extracts a sub expression, encapsulates it, and safely moves it into a separate function.

Some older style compilers use Lambda Lifting as a compilation step in implementing a functional language.

Influence on other languages

Lambda Calculus has directly influenced function languages such as ML and Haskell. It has also influence many imperative languages, by providing the motivation for features. For example:

• Closures
• Anonymous functions
• Reified functions. Functions as First-class citizen.

Semantics

Deductive Lambda Calculus

Deductive Lambda Calculus

Denotational Semantics

The fact that lambda calculus terms act as functions on other lambda calculus terms, and even on themselves, led to questions about the semantics of the lambda calculus. Could a sensible meaning be assigned to lambda calculus terms? The natural semantics was to find a set D isomorphic to the function space D → D, of functions on itself. However, no nontrivial such D can exist, by cardinality constraints because the set of all functions from D into D has greater cardinality than D.

In the 1970s, Dana Scott showed that, if only continuous functions were considered, a set or domain D with the required property could be found, thus providing a model for the lambda calculus.

This work also formed the basis for the denotational semantics of programming languages.

Typed lambda calculus

Main article: Typed lambda calculus

The Lambda calculus defined in this article has no type declarations. All lambda expressions represent functions, but the type of the function is not explicitly declared. Various type systems may be added to Lambda Calculus, to both constrain it and give it more expressive power. Lambda Calculus, with a type systems is the basis for functional languages, such as ML and Haskell.

Typed lambda calculus is the study of type systems for Lambda Calculus. The Lambda cube is a framework for studying type systems, starting with the Simply typed lambda calculus.

Normal forms and confluence

Main article: Normalization property (abstract rewriting)

The evaluation of Lambda calculus is defined by Beta Reductions, which may be considered as rewrite rules. That is, the execution of the Lambda calculus proceeds by a series of Beta Reduction steps to transform the program into the calculated value.

A rewrite system may be,

• Strongly normalizing; Every sequence of rewrites eventually terminates to a term in normal form.
• Weak normalization; For each term, there exists at least one particular sequence of rewrites that eventually yields a normal form.

Considered as a rewriting rule, β-reduction is neither strongly normalising nor weakly normalising.

β-reduction is confluent, which means there is more than one way of writing the calculation at a particular state in the computation. This is because α-conversion, can rename variables.

Computability

Lambda Calculus is Turing Complete

Lambda Calculus is Turing complete without any extensions or types being added to the language. All normal forms (values) in Lambda Calculus however functions. However Church showed that by using some functions to represent other values such as Boolean or integer. In this way he showed that Lambda Calculus is Turing Complete. This is the Church-Turing thesis for a discussion of other approaches and their equivalence.

Undecidability of equivalence

There is no computable algorithm that can determine whether or not two lambda expressions are equivalent. This was historically the first problem for which undecidability could be proven. As is common for a proof of undecidability, the proof shows that no computable function can decide the equivalence. Church's thesis is then invoked to show that no algorithm can do so.

Church's proof reduces the problem to determining whether a given lambda expression has a normal form. A normal form is an equivalent expression that cannot be reduced any further under the rules imposed by the form.

Then he assumes that this predicate is computable, and can hence be expressed in lambda calculus. Building on earlier work by Kleene and constructing a Gödel numbering for lambda expressions, he constructs a lambda expression e that closely follows the proof of Gödel's first incompleteness theorem. If e is applied to its own Gödel number, a contradiction results.

Implementation

Reduction strategies

Further information: Evaluation strategy

Whether a term is normalizing or not, and how much work needs to be done in normalizing it if it is, depends to a large extent on the reduction strategy used. The distinction between reduction strategies relates to the distinction in functional programming languages between eager evaluation and lazy evaluation.

Strict/eager evaluation strategies

Most programming languages (including Lisp, ML and imperative languages like C and Java) are described as "strict", meaning that functions applied to non-normalising arguments are non-normalising. This is done essentially using applicative order, call by value reduction (see below), but usually called "eager evaluation".

Applicative order

The rightmost, innermost redex is always reduced first. Intuitively this means a function's arguments are always reduced before the function itself. Applicative order always attempts to apply functions to normal forms, even when this is not possible.

Applicative order is not a normalizing strategy. The usual counterexample is as follows: define Ω = ωω where ω = λx.xx. This entire expression contains only one redex, namely the whole expression; its beta-reduction is again Ω. Since this is the only available reduction, Ω has no normal form (under any evaluation strategy). Using applicative order, the expression KIΩ = (λx.λy.x) (λx.x)Ω is reduced by first reducing Ω to normal form (since it is the rightmost redex), but since Ω has no normal form, applicative order fails to find a normal form for KIΩ.

The positive trade-off of using applicative order is that it does not cause unnecessary computation, if all arguments are used, because it never substitutes arguments containing redexes and hence never needs to copy them (which would duplicate work). In the above example, in applicative order (λx.xx) ((λx.x)y) reduces first to (λx.xx)y and then to the normal order yy, taking two steps instead of three.

Call by value

Only the outermost redexes are reduced: a redex is reduced only when its right hand side has reduced to a value (variable or lambda abstraction).

Lazy evaluation strategies

Most purely functional programming languages (notably Miranda and its descendents, including Haskell), and the proof languages of theorem provers, use lazy evaluation, which is essentially the same as call by need.

Normal order

The leftmost, outermost redex is always reduced first. Whenever possible the arguments are substituted into the body of an abstraction before the arguments are reduced.

Normal order is so called because it always finds a normalising reduction, if one exists. In the above example, KIΩ reduces under normal order to I, a normal form. A drawback is that redexes in the arguments may be copied, resulting in duplicated computation (for example, (λx.xx) ((λx.x)y) reduces to ((λx.x)y) ((λx.x)y) using this strategy; now there are two redexes, so full evaluation needs two more steps, but if the argument had been reduced first, there would now be none).

Call by name

As normal order, but no reductions are performed inside the body of abstractions. For example λx.(λx.x)x is in normal form according to this strategy, although it contains the redex (λx.x)x.

Call by need

As normal order, but function applications that would duplicate terms instead name the argument, which is then reduced only "when it is needed". Called in practical contexts "lazy evaluation". In implementations this "name" takes the form of a pointer, with the redex represented by a thunk.

For example, (λx.xx) ((λx.x)y) reduces to ((λx.x)y) ((λx.x)y), which has two redexes, but in call by need they are represented using the same object rather than copied, so when one is reduced the other is too.

Parallel evaluation strategies

The Church-Rosser property of the lambda calculus means that evaluation (β-reduction) can be carried out in any order, even in parallel. This means that various parallel evaluation strategies are possible.

Unordered beta reductions

Any redex can be reduced at any time. This means essentially the lack of any particular reduction strategy.

Parallelism and concurrency

The following strategies are related to Lambda Calculus.

• Futures
• process calculi

Director Strings Optimization

Main article: Director string

While the idea of beta reduction seems simple enough, it is computationally expensive. The interpreter must find the location of all of the occurrences of the bound variable V in the expression E. As an optimization the interpreter may track the locations of free variables, which has a space cost.

A naïve search for the locations of V in E is O(n) in the length n of E. This has led to the study of systems that use explicit substitution. Sinot's director strings offer a way of tracking the locations of free variables in expressions.

See also

• Applicative computing systems – Treatment of objects in the style of the lambda calculus
• Binary lambda calculus – A version of lambda calculus with binary I/O, a binary encoding of terms, and a designated universal machine.
• Calculus of constructions – A typed lambda calculus with types as first-class values
• Cartesian closed category – A setting for lambda calculus in category theory
• Categorical abstract machine – A model of computation applicable to lambda calculus
• Combinatory logic – A notation for mathematical logic without variables
• Curry–Howard isomorphism – The formal correspondence between programs and proofs
• Domain theory – Study of certain posets giving denotational semantics for lambda calculus
• Evaluation strategy – Rules for the evaluation of expressions in programming languages
• Explicit substitution – The theory of substitution, as used in β-reduction
• Harrop formula – A kind of constructive logical formula such that proofs are lambda terms
• Kappa calculus – A first-order analogue of lambda calculus
• Kleene–Rosser paradox – A demonstration that some form of lambda calculus is inconsistent
• Knights of the Lambda Calculus – A semi-fictional organization of LISP and Scheme hackers
• Lambda cube – A framework for some extensions of typed lambda calculus
• Lambda-mu calculus – An extension of the lambda calculus for treating classical logic
• Rewriting – Transformation of formulæ in formal systems
• SECD machine – A virtual machine designed for the lambda calculus
• Simply typed lambda calculus - Version(s) with a single type constructor
• SKI combinator calculus – A computational system based on the S, K and I combinators
• System F – A typed lambda calculus with type-variables
• Typed lambda calculus – Lambda calculus with typed variables (and functions)
• Universal Turing machine – A formal computing machine that is equivalent to lambda calculus
• Unlambda – An esoteric functional programming language based on combinatory logic

Further reading

• Abelson, Harold & Gerald Jay Sussman. Structure and Interpretation of Computer Programs. The MIT Press. ISBN 0-262-51087-1.
• Hendrik Pieter Barendregt Introduction to Lambda Calculus.
• Henk Barendregt, The Impact of the Lambda Calculus in Logic and Computer Science. The Bulletin of Symbolic Logic, Volume 3, Number 2, June 1997.
• Barendregt, Hendrik Pieter, The Type Free Lambda Calculus pp1091–1132 of Handbook of Mathematical Logic, North-Holland (1977) ISBN 0-7204-2285-X
• Cardone and Hindley, 2006. History of Lambda-calculus and Combinatory Logic. In Gabbay and Woods (eds.), Handbook of the History of Logic, vol. 5. Elsevier.
• Church, Alonzo, An unsolvable problem of elementary number theory, American Journal of Mathematics, 58 (1936), pp. 345–363. This paper contains the proof that the equivalence of lambda expressions is in general not decidable.
• Kleene, Stephen, A theory of positive integers in formal logic, American Journal of Mathematics, 57 (1935), pp. 153–173 and 219–244. Contains the lambda calculus definitions of several familiar functions.
• Landin, Peter, A Correspondence Between ALGOL 60 and Church's Lambda-Notation, Communications of the ACM, vol. 8, no. 2 (1965), pages 89–101. Available from the ACM site. A classic paper highlighting the importance of lambda calculus as a basis for programming languages.
• Larson, Jim, An Introduction to Lambda Calculus and Scheme. A gentle introduction for programmers.
• Schalk, A. and Simmons, H. (2005) An introduction to λ-calculi and arithmetic with a decent selection of exercises. Notes for a course in the Mathematical Logic MSc at Manchester University.
• de Queiroz, Ruy J.G.B. (2008) On Reduction Rules, Meaning-as-Use and Proof-Theoretic Semantics. Studia Logica, 90(2):211-247. A paper giving a formal underpinning to the idea of ‘meaning-is-use’ which, even if based on proofs, it is different from proof-theoretic semantics as in the Dummett–Prawitz tradition since it takes reduction as the rules giving meaning.

Monographs/textbooks for graduate students:

• Morten Heine Sørensen, Paweł Urzyczyn, Lectures on the Curry-Howard isomorphism, Elsevier, 2006, ISBN 0-444-52077-5 is a recent monograph that covers the main topics of lambda calculus from the type-free variety, to most typed lambda calculi, including more recent developments like pure type systems and the lambda cube. It does not cover subtyping extensions.
• Pierce, Benjamin (2002), Types and Programming Languages, MIT Press, ISBN 0-262-16209-1 covers lambda calculi from a practical type system perspective; some topics like dependent types are only mentioned, but subtyping is an important topic.

Some parts of this article are based on material from FOLDOC, used with permission.

External links

• Achim Jung, A Short Introduction to the Lambda Calculus-(PDF)
• Dana Scott, A timeline of lambda calculus-(PDF)
• David C. Keenan, To Dissect a Mockingbird: A Graphical Notation for the Lambda Calculus with Animated Reduction
• Raúl Rojas, A Tutorial Introduction to the Lambda Calculus-(PDF)
• Peter Selinger, Lecture Notes on the Lambda Calculus-(PDF)
• L. Allison, Some executable λ-calculus examples
• Georg P. Loczewski, The Lambda Calculus and A++
• Bret Victor, Alligator Eggs: A Puzzle Game Based on Lambda Calculus
• Lambda Calculus on Safalra’s Website
• "Lambda Calculus". PlanetMath.
• LCI Lambda Interpreter a simple yet powerful pure calculus interpreter
• Lambda Calculus links on Lambda-the-Ultimate
• Mike Thyer, Lambda Animator, a graphical Java applet demonstrating alternative reduction strategies.
• An Introduction to Lambda Calculus and Scheme, by Jim Larson
• Implementing the Lambda calculus using C++ Templates

Category:1936 in computing Category:American inventions Category:Articles with example code Category:Computability theory Category:Formal methods Category:Models of computation Category:Theoretical computer science