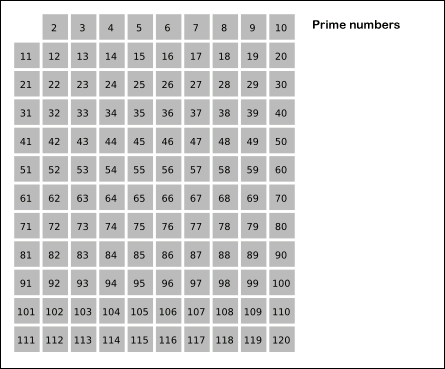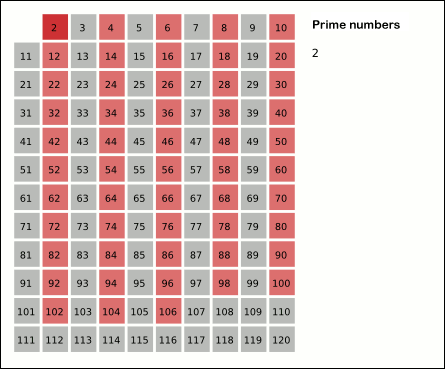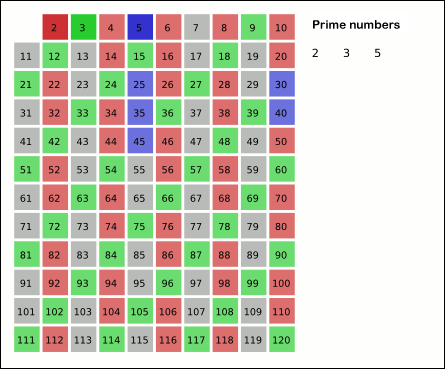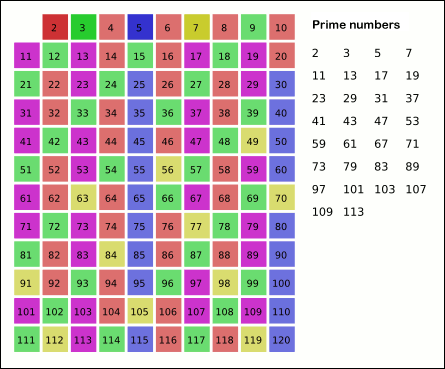
User:WillNess/Sieve of Eratosthenes

Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square).

In mathematics, the sieve of Eratosthenes (Greek: κόσκινον Ἐρατοσθένους), one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e. not prime) the multiples of each prime, starting with the multiples of 2.^[1]

The multiples of a given prime are generated starting from that prime, as a sequence of numbers with the same difference, equal to that prime, between consecutive numbers.^[1] Thus each composite is found from its prime factors only. This is the key to the sieve's efficiency, and its key distinction from using trial division to test each candidate number for divisibility by each prime in the sequence of primes, from the lowest up.^[2]

The sieve of Eratosthenes is one of the most efficient ways to find all of the smaller primes (below 10 million or so).^[3] It is named after Eratosthenes of Cyrene, an ancient Greek mathematician; although none of his works have survived, the sieve was described and attributed to Eratosthenes in the Introduction to Arithmetic by Nicomachus.^[4]

Algorithm description edit

Sift the Two's and Sift the Three's,
The Sieve of Eratosthenes.
When the multiples sublime,
The numbers that remain are Prime.

Anonymous^[5]^[6]^[7]

A prime number is a natural number which has exactly two distinct natural number divisors: 1 and itself.

To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:

Create a list of consecutive integers from 2 to n: (2, 3, 4, ..., n).
Initially, let p equal 2, the first prime number.
Starting from p, count up in increments of p and mark each of these numbers greater than p itself in the list. These numbers will be 2p, 3p, 4p, etc.; note that some of them may have already been marked.
Find the first number greater than p in the list that is not marked; let p now equal this number (which is the next prime).
If there were no more unmarked numbers in the list, stop. Otherwise, repeat from step 3.

When the algorithm terminates, all the numbers in the list that are not marked are prime.

As a refinement, it is sufficient to mark the numbers in step 3 starting from p², as all the smaller multiples of p will have already been marked at that point. This means that the algorithm is allowed to terminate in step 5 when p² is greater than n.^[1]

\textstyle \mathbb {P} =\{2,3,4...\}\setminus \,\bigcup \,\,\{\{2p,\,3p,\,4p,\,...\}:p\in \mathbb {P} \}

\textstyle \mathbb {P} =\{2,3,4...\}\setminus \,\bigcup \,\,\{\{p^{2},\,p^{2}+p,\,p^{2}+2p,\,...\}:p\in \mathbb {P} \}

\textstyle \mathbb {P} =\{2,3,4...\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p^{2},\,p^{2}+p,\,p^{2}+2p,\,...\}

\textstyle \mathbb {P} =\{2,3...\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p^{2},\,p^{2}+p,\,...\}

\textstyle \mathbb {P} =\{2,3,4...\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\,n:n\in \{2,\,3,\,4,\,...\}\}

\textstyle \mathbb {P} =\{2,3...\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\,n:n\in \{p,\,p+1,\,...\}\}

\textstyle \mathbb {P} =\{n\in \mathbb {N} :n\geq 2\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\,n:n\in \mathbb {N} ,n\geq 2\}

\textstyle \mathbb {P} =\{n\in \mathbb {N} :n\geq 2\}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\,n:n\in \mathbb {N} ,n\geq p\}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\,n:n\in \mathbb {N} _{p}\}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\bigcup _{p\in \mathbb {P} }\{p\cdot \mathbb {N} _{p}\}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\bigcup _{m\in \mathbb {N} _{2}}\{m\,n:n\in \mathbb {N} _{m}\}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\bigcup _{m\in \mathbb {N} _{2}}\{m\,n:n\in \mathbb {N} _{2}\}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\mathbb {N} _{2}\cdot \mathbb {N} _{2}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\mathbb {P} \cdot \mathbb {N} _{2}

\textstyle \mathbb {P} =\mathbb {N} _{2}\setminus \,\mathbb {P} \cdot \mathbb {N} _{_{\mathbb {P} }}

Another refinement is to initially list odd numbers only, (3, 5, ..., n), and count up using an increment of 2p in step 3, thus marking only odd multiples of p greater than p itself. This actually appears in the original algorithm.^[1]^[8] This can be generalized with wheel factorization, forming the initial list only from numbers coprime with the first few primes and not just from odds, i.e. numbers coprime with 2.^[9]

Incremental sieve edit

An incremental formulation of the sieve^[2] generates primes indefinitely (i.e., without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime p are generated directly by counting up from the square of the prime in increments of p (or 2p for odd primes). The generation must be initiated only when the prime's square is reached to avoid adverse effects on efficiency. It can be expressed symbolically under the dataflow paradigm as

primes = [2, 3, ...] \ [[p*p, p*p+p, ...] for p in primes] = [2, 3, ...] \ [ [4, 6, 8, ...], [9, 12, 15, ...], ... ] = [2, 3, 5, 7, 11, 13, 17, ...],

using list comprehension notation with \ denoting set subtraction of arithmetic progressions of numbers.

 primes = sieve [2..] where
          sieve [p, ...xs] = [p, ...sieve (xs \ [p, p+p..])]
          sieve [p, ...xs] = [p, ...sieve (xs \ [p², p²+p..])]
          sieve [p, ...xs] = [p, ...sieve (xs \ [p*n for n in [p..]])]
          sieve [p, ...xs] = [p, ...sieve (xs \ p * [p..])]

 primes = sieve [2..] where
          sieve [p, ...xs] = [p, ...sieve (xs \ [p*n for n in [p, ...xs]])]
          sieve [p, ...xs] = [p, ...sieve (xs \ [p², ...[p*n for n in xs]])]
          sieve [p, ...xs] = [p, ...sieve (xs \ [p², ...p * xs])]
          sieve [p, ...xs] = [p, ...sieve (xs \ p * [p, ...xs])]

 primes = [2, ...sieve primes [3..]] where
          sieve [p, ...ps] [...h, p², ...xs] =
                         = [...h, ...sieve ps (xs \ [p², p²+p..])]
                         = [...h, ...sieve ps [x in xs if x%p > 0]]

 primes = [2, ...[3..] \ [ [p², p²+p..] for p in primes ]]

 primes = 2 : sieve primes [3..]  where
    sieve (p:ps)
          (span (< p*p) -> (h, xs))
                 = h ++ sieve ps [x | x <- xs, mod x p > 0]
                 = h ++ sieve ps (minus xs [p*p, p*p+p..])

 primes = sieve [2..]  where
    sieve (p:xs)
                 = [p] ++ sieve [x | x <- xs, mod x p > 0]
                 = [p] ++ sieve (minus xs [p, p+p..])
                 = [p] ++ sieve (minus xs (map (p*) [2..]))
                 = [p] ++ sieve (minus xs (map (p*) [p..]))
                 = [p] ++ sieve (minus xs [p*p, p*p+p..])
                 = [p] ++ sieve (minus xs (map (p*) (p:xs)))

Or in Haskell,

{-# LANGUAGE ViewPatterns #-} import Data.List.Ordered (minus, union, foldt) primes = sieve [2..] where -- sieve (p:t) sieve (splitAt 1 -> ([p],t)) = [p] ++ sieve (t `minus` [p, p+p..]) = [p] ++ sieve (t `minus` [p+p, p+p+p..]) = [p] ++ sieve (t `minus` [p*p, p*p+p..]) -- Eratosthenes' = [p] ++ sieve (t `minus` map (p*) [p..]) = [p] ++ sieve (t `minus` map (p*) (p:t)) -- Euler's = [p] ++ sieve [x | x <- t, rem x p > 0] -- Turner's

or, better,

primes = 2 : sieve primes [3..] where sieve (p:ps) (span (< p*p) -> (hs,t)) = hs ++ sieve ps (t `minus` [p*p, p*p+p..]) -- postponed Er' = hs ++ sieve ps [x | x <- t, rem x p > 0] -- postponed Tr' = 2 : sieve [[p*p, p*p+p..] | p <- primes] [3..] where sieve (ms@(q:_):cs) (span (< q) -> (hs,t)) = hs ++ sieve cs (t `minus` ms)

which is also

primes = [h | (h:_) <- scanl minus [2..] [[p, p+p..] | p <- primes]] = 2 : [h | (h:_) <- scanl (minus . drop 1) [3,5..] [[p*p, p*p+2*p..] | p <- tail primes]] = [2] ++ minus [3..] (foldr (\(x:xs) -> (x :) . union xs) [] -- Richard Bird's, [[p*p, p*p+p..] | p <- primes]) = [2,3] ++ minus [5,7..] -- on odds, (foldr (\(x:xs) -> (x :) . union xs) [] [[p*p, p*p+2*p..] | p <- tail primes]) = [2,3] ++ minus [5,7..] -- tree-folded (foldt (\(x:xs) -> (x :) . union xs) [] [[p*p, p*p+2*p..] | p <- tail primes])

Trial division can also be used to produce primes indefinitely by filtering out the composite numbers found by testing each candidate number for divisibility by its preceding primes. It is not the sieve of Eratosthenes but is often confused with it, even though the sieve of Eratosthenes directly generates the composites instead of testing for them. Trial division has worse theoretical complexity than that of the sieve of Eratosthenes in generating ranges of primes.^[2]

When testing each candidate number, the optimal trial division algorithm uses just those prime numbers not exceeding its square root:

 primes = [2, ...sieve primes [3..]] where
          sieve [p, ...ps] [...h, p², ...xs] =
                           [...h, ...sieve ps [x in xs if not (x%p == 0)]]

The widely known 1975 functional sieve code by David Turner^[10] is often presented as an example of the sieve of Eratosthenes^[9] but is actually a sub-optimal trial division algorithm:^[2]

 primes = sieve [2..] where
          sieve [p, ...xs] = [p, ...sieve [x in xs if x%p > 0]]

An incremental formulation of the sieve^[2] generates primes indefinitely (i.e. without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime p are generated directly, by counting up from the square of the prime in increments of p (or 2p for odd primes):

 primes = [2, ...([3..] \ [ [p², p²+p..] | p <- primes ])]

 first primes = 2 
 rest  primes = primes & map (\p -> [p*p, p*p+p..]) >>> unions >>> minus [3..]
              = [3..] `minus` unions [[p*p, p*p+p..] | p <- primes]
              = [3..] `minus` [4,6..] 
                       `minus` unions [[p*p, p*p+p..] | p <- drop 1 primes]
              = [3,5..] 
                       `minus` unions [[p*p, p*p+2*p..] | p <- drop 1 primes]
              = [3,5..] `minus` [9,15..] 
                         `minus` unions [[p*p, p*p+2*p..] | p <- drop 2 primes]
              ......

Or, in corecursive notation,

 primes = eratos [2..]
          where
          first (eratos xs) = first xs
          rest  (eratos xs) = let p = first xs in
                                eratos (rest xs `minus` [p+p, p+p+p..])
                             -- eratos (rest xs `minus` [p*p, p*p+p..])
                             -- eratos (rest xs `minus` [p*n | n <- [p..]])

Trial division edit

Trial division can be used to produce primes by filtering out the composites found by testing each candidate number for divisibility by its preceding primes. It is often confused with the sieve of Eratosthenes, although the latter directly generates the composites instead of testing for them. Trial division has worse theoretical complexity than that of the sieve of Eratosthenes in generating ranges of primes.^[2]

When testing each candidate number, the optimal trial division algorithm uses just those prime numbers not exceeding its square root. The widely known 1975 functional code by David Turner^[11] is often presented as an example of the sieve of Eratosthenes^[9] but is actually a sub-optimal trial division algorithm:^[2]

 primes = turner [2..]
          where
          first (turner xs) = first xs
          rest  (turner xs) = let p = first xs in
                                turner [x | x <- rest xs, rem x p > 0]
                             -- eratos (rest xs `minus` [p+p, p+p+p..])
                             -- eratos (rest xs `minus` [p*p, p*p+p..])

Example edit

To find all the prime numbers less than or equal to 30, proceed as follows.

First generate a list of integers from 2 to 30:

 2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

First number in the list is 2; cross out every 2nd number in the list after it (by counting up in increments of 2), i.e. all the multiples of 2:

 2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Next number in the list after 2 is 3; cross out every 3-rd number in the list after it (by counting up in increments of 3), i.e. all the multiples of 3:

 2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Next number not yet crossed out in the list after 3 is 5; cross out every 5-th number in the list after it (by counting up in increments of 5), i.e. all the multiples of 5:

 2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7-th number in the list after it, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7*7 is greater than 30. The numbers left not crossed out in the list at this point are all the prime numbers below 30:

 2  3     5     7           11    13          17    19          23                29

Algorithm complexity edit

Time complexity in the random access machine model is $O(n\log \log n)$ operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches $\log \log n$ .

The bit complexity of the algorithm is $O(n(\log n)(\log \log n))$ bit operations with a memory requirement of $O(n)$ .^[12]

The segmented version of the sieve of Eratosthenes, with basic optimizations, uses $O(n)$ operations and $O(n^{1/2}\log \log n/\log n)$ bits of memory.^[13]

Implementation edit

Symbolically, under dataflow paradigm with list comprehension notation, it is

 primes = [2, 3, ...] \ [[p*p, p*p+p, ...], ... for p in primes]

 = [2, 3, ...] 
     \ 
     [ [4, 6, 8, 10, 12, ...],
               [9,   12,  15, ...], 
                        ...
                            [p*p, p*p+p, ...],
                                    ... for p in primes]
 = [2, 3, 5, 7,    11, 13,   17, 19,   23, ...]

or

    <--.-- [2..] \ [[p*p, p*p+p..] | p <---. ]              
      /                                     \
      \_____________________________________/

   fix $ ([2..] \) . map (\p -> [p*p, p*p+p..])

   primes = [2..] \ [[p*p, p*p+p..] | p <- primes]

   oddprs = [3,5..] \ [[p*p, p*p+2*p..] | p <- oddprs]

Pseudocode edit

In pseudocode:^[14]

Input: an integer n > 1
 
Let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
 
for i = 2, 3, 4, 5, ...,  $\sqrt n$  :
  if A[i] is true:
    for j = i², i²+i, i²+2i, ..., n:
      A[j] := false
 
Output: all i such that A[i] is true.
 
For odds only, setting aside 2 as the only even prime, it is
 
for i = 3, 5, 7, 9, ...,  $\sqrt n$  :
  if A[i] is true:
    for j = i², i²+2i, i²+4i, ..., n:
      A[j] := false

Large ranges may not fit entirely in memory. In these cases it is necessary to use a segmented sieve where only portions of the range are sieved at a time.^[15] For ranges so large that the sieving primes could not be held in memory, space-efficient sieves like that of Sorenson are used instead.^[16]

Arithmetic progressions edit

The sieve may be used to find primes in arithmetic progressions.^[17]

Euler's sieve edit

Euler's proof of the zeta product formula contains version of the sieve of Eratosthenes in which each composite number is eliminated exactly once.^{[citation needed]} It, too, starts with a list of numbers from 2 to n in order. On each step the first element is identified as the next prime and the results of multiplying this prime with each element of the list are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated:

 primes = sieve [2..]
   where
   sieve [p, ...xs] =
         [p, ...sieve (xs \ [p*n for n in [p, ...xs]])]

\textstyle \mathbb {E_{1}} =\{2\,,3\,,4\,...\}

\textstyle \mathbb {E_{2}} =\mathbb {E_{1}} \setminus \,\{p\,n:p\in \{first(\mathbb {E_{1}} )\},n\in \{1\}\cup \mathbb {E_{1}} \}

......

\textstyle \mathbb {E_{i+1}} =\mathbb {E_{i}} \setminus \,\{p\,n:p\in \{first(\mathbb {E_{i}} )\},n\in \{1\}\cup \mathbb {E_{i}} \}

......

primes = map head . iterate (\(p:xs) -> xs `minus` map (p*) (p:xs)) $ [2..]

An example, calculating primes below 80:

2:  (3) 5  7  9  11  13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79  ...
3:     (5) 7     11  13    17 19    23 25    29 31    35 37    41 43    47 49    53 55    59 61    65 67    71 73    77 79  ...
4:        (7)    11  13    17 19    23       29 31       37    41 43    47 49    53       59 61       67    71 73    77 79  ...
5:              (11) 13    17 19    23       29 31       37    41 43    47       53       59 61       67    71 73       79  ...
.....

Here the example is shown starting from odds, after the 1st step of the algorithm. Thus on kth step all the remaining multiples of the kth prime are removed from the list, which will thereafter contain only numbers coprime with the first k primes (cf. Wheel factorization), so that the list will start with the next prime, and all the numbers in it below the square of its first element will be prime too.

Thus when generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime. In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.

Note that numbers that will be discarded by some step are still used while marking the multiples, e.g. for the multiples of 3 it is $3 \cdot 3 = 9$ , $3 \cdot 5 = 15$ , $3 \cdot 7 = 21$ , $3 \cdot 9 = 27$ , ..., $3 \cdot 15 = 45$ , ... :

 primes = eulers [2..]
          where
          first (eulers xs) = first xs
          rest  (eulers xs) = let p = first xs in
                                eulers (     xs `minus` [p*n | n <- 1:xs])
                             -- eulers (rest xs `minus` [p*n | n <- xs])
                             -- eratos (rest xs `minus` [p*n | n <- [p..])
                             -- turner [x | x <- rest xs, rem x p > 0]

References edit

^ ^a ^b ^c ^d Horsley, Rev. Samuel, F. R. S., "Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an Account of His Method of Finding All the Prime Numbers," Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.
^ ^a ^b ^c ^d ^e ^f ^g O'Neill, Melissa E., "The Genuine Sieve of Eratosthenes", Journal of Functional Programming, Published online by Cambridge University Press 9 October 2008 doi:10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird). Cite error: The named reference "ONeill" was defined multiple times with different content (see the help page).
^ The Prime Glossary: "The Sieve of Eratosthenes", http://primes.utm.edu/glossary/page.php?sort=SieveOfEratosthenes, references 16. November 2008.
^ Nicomachus, Introduction to Arithmetic, I, 13. [1]
^ Clocksin, William F., Christopher S. Mellish, Programming in Prolog, 1981, p. 174. ISBN 3540110461.
^ Merritt, Doug (December 14, 2008). "Sieve Of Eratosthenes". Retrieved 2009-03-26.
^ Nykänen, Matti (October 26, 2007). "An Introduction to Functional Programming with the Programming Language Haskell" (PDF). Retrieved 2009-03-26.
^ Nicomachus, ibid., p. 31, where only odd numbers appear in the table.
^ ^a ^b ^c Colin Runciman, "FUNCTIONAL PEARL: Lazy wheel sieves and spirals of primes", Journal of Functional Programming, Volume 7 Issue 2, March 1997; also here.
^ Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (sieve (p:xs) = p : sieve [x | x <- xs, rem x p > 0] ; primes = sieve [2..]). But see also Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976, where we find the following, attributed to P. Quarendon: primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; the priority is unclear.
^ Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975.
^ Pritchard, Paul, "Linear prime-number sieves: a family tree," Sci. Comput. Programming 9:1 (1987), pp. 17–35.
^ A. O. L. Atkin and D. J. Bernstein, "Prime sieves using binary quadratic forms", Mathematics of Computation 73 (2004), pp. 1023–1030.
^ Sedgewick, Robert (1992). Algorithms in C++. Addison-Wesley. ISBN 0-201-51059-6. {{cite book}}: |access-date= requires |url= (help), p. 16.
^ Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–124.
^ J. Sorenson, The pseudosquares prime sieve, Proceedings of the 7th International Symposium on Algorithmic Number Theory. (ANTS-VII).
^ J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.

External links edit

[[Category:Primality tests]] [[Category:Articles with example pseudocode]] [[Category:Sieve theory| ]] [[Category:Algorithms]]

[horsley-1] Horsley, Rev. Samuel, F. R. S., "Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an Account of His Method of Finding All the Prime Numbers," Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.

[ONeill-2] ^ ^a ^b ^c ^d ^e ^f ^g O'Neill, Melissa E., "The Genuine Sieve of Eratosthenes", Journal of Functional Programming, Published online by Cambridge University Press 9 October 2008 doi:10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird). Cite error: The named reference "ONeill" was defined multiple times with different content (see the help page).

[3] The Prime Glossary: "The Sieve of Eratosthenes", http://primes.utm.edu/glossary/page.php?sort=SieveOfEratosthenes, references 16. November 2008.

[4] Nicomachus, Introduction to Arithmetic, I, 13. [1]

[5] Clocksin, William F., Christopher S. Mellish, Programming in Prolog, 1981, p. 174. ISBN 3540110461.

[6] Merritt, Doug (December 14, 2008). "Sieve Of Eratosthenes". Retrieved 2009-03-26.

[7] Nykänen, Matti (October 26, 2007). "An Introduction to Functional Programming with the Programming Language Haskell" (PDF). Retrieved 2009-03-26.

[8] Nicomachus, ibid., p. 31, where only odd numbers appear in the table.

[Runciman-9] Colin Runciman, "FUNCTIONAL PEARL: Lazy wheel sieves and spirals of primes", Journal of Functional Programming, Volume 7 Issue 2, March 1997; also here.

[10] Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (sieve (p:xs) = p : sieve [x | x <- xs, rem x p > 0] ; primes = sieve [2..]). But see also Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976, where we find the following, attributed to P. Quarendon: primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; the priority is unclear.

[11] Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975.

[12] Pritchard, Paul, "Linear prime-number sieves: a family tree," Sci. Comput. Programming 9:1 (1987), pp. 17–35.

[13] A. O. L. Atkin and D. J. Bernstein, "Prime sieves using binary quadratic forms", Mathematics of Computation 73 (2004), pp. 1023–1030.

[sedgewick-14] Sedgewick, Robert (1992). Algorithms in C++. Addison-Wesley. ISBN 0-201-51059-6. {{cite book}}: |access-date= requires |url= (help), p. 16.

[15] Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–124.

[16] J. Sorenson, The pseudosquares prime sieve, Proceedings of the 7th International Symposium on Algorithmic Number Theory. (ANTS-VII).

[17] J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

v t e Number-theoretic algorithms
Primality tests	AKS APR Baillie–PSW Elliptic curve Pocklington Fermat Lucas Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin
Prime-generating	Sieve of Atkin Sieve of Eratosthenes Sieve of Pritchard Sieve of Sundaram Wheel factorization
Integer factorization	Continued fraction (CFRAC) Dixon's Lenstra elliptic curve (ECM) Euler's Pollard's rho p − 1 p + 1 Quadratic sieve (QS) General number field sieve (GNFS) Special number field sieve (SNFS) Rational sieve Fermat's Shanks's square forms Trial division Shor's
Multiplication	Ancient Egyptian Long Karatsuba Toom–Cook Schönhage–Strassen Fürer's
Euclidean division	Binary Chunking Fourier Goldschmidt Newton-Raphson Long Short SRT
Discrete logarithm	Baby-step giant-step Pollard rho Pollard kangaroo Pohlig–Hellman Index calculus Function field sieve
Greatest common divisor	Binary Euclidean Extended Euclidean Lehmer's
Modular square root	Cipolla Pocklington's Tonelli–Shanks Berlekamp Kunerth
Other algorithms	Chakravala Cornacchia Exponentiation by squaring Integer square root Integer relation (LLL; KZ) Modular exponentiation Montgomery reduction Schoof Trachtenberg system
Italics indicate that algorithm is for numbers of special forms