User:Thepigdog/Lambda Calculus

The lowercase lambda, the 11th letter of the Greek alphabet, is used to symbolize the lambda calculus.

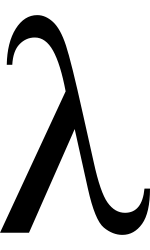
Lambda calculus is a programming language based solely on lambda abstraction and function application.

Normally, in defining a function, the formal parameters are written after the function name. The Lambda Abstraction is an alternative representation that associates the formal parameters of a function with the expression that implements the function. This allows a function to be defined as an expression.

Today, the lambda calculus has applications in many different areas in mathematics, philosophy, linguistics, and computer science. Lambda calculus has played an important role in the development of the theory of programming languages and in the development of functional programming languages.

The lambda calculus also has many applications in proof theory. A major example of this is the Curry–Howard correspondence, which gives a correspondence between different systems of typed lambda calculus and systems of formal logic.

History

Alonzo Church invented the Lambda Calculus in the 1930s, originally to provide a new and simpler basis for mathematics. However soon after inventing it major logic problems were identified with the definition of the Lambda Abstraction.

The Kleene–Rosser paradox is an implementation of Richard's paradox in combinatory logic. Combinatory Logic is closely related to Lambda Calculus. Haskell Curry found that the key step in this paradox could be used to implement the simpler Curry's Paradox. The existence of this paradox meant that the Combinatory Logic, and Lambda Calculus, could not be both consistent and complete as a deductive system.

Alonzo Church then used the lambda Calculus as a programming language to formalized the concept of effective computability. In 1936, Alonzo Church and Alan Turing published independent papers showing that a general solution to the Entscheidungsproblem is impossible, assuming that the intuitive notation of "effectively calculable" is captured by the functions computable by a Turing machine (or equivalently, by those expressible in the lambda calculus). This assumption is now known as the Church–Turing thesis.

Lambda calculus is a simple universal model of computation. Turing showed in 1937 that any program written for a Turing machines could be written in lambda calculus and vice versa.

Peter Landin's 1965 paper A Correspondence between ALGOL 60 and Church's Lambda-notation, sequential procedural programming languages can be understood in terms of the lambda calculus, which provides the basic mechanisms for procedural abstraction and procedure (subprogram) application.

Introduction

Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application using variable binding and substitution. The name derives from the Greek letter lambda (λ) used to denote binding a variable in a function.

Lambda calculus is used and viewed in many ways,

Usages and viewpoints on the lambda calculus

Pure lambda calculus	An isolated mathematical system based on lambda abstraction.
Model for computing	Data types, arithmetic, and Church encoding and Mogensen–Scott encoding.
Simply typed lambda calculus	Lambda calculus, with a simple type system based on function mappings.
Typed lambda calculus	Lambda calculus with a properly defined type system.
A basis for functional programming languages.	Most functional languages are based heavily on the lambda calculus.
Illative lambda calculus	The lambda abstraction as an extra operator in mathematics.

Explanation

A lambda term represents a function that may be reduced until it cannot be reduced any further. It is then said to be in normal form. Informally it is then a "value". For example,

(λn.λf.λx.f (n f x)) λf.λx.f (f (f x)))

In this term, the abstraction λn represents a parameter. The term λf.λx.f (f (f x))) is bound to the parameter n giving it a value. Then every (in this case one) occurrence of n in λf.λx.f (n f x) is replaced by λf.λx.f (f (f x))), giving,

λf.λx.f (λf.λx.f (f (f x))) f x)

This step is called beta reduction. The step is repeated on the sub term λf.λx.f (f (f x))) f x. Here

f is replaced by f in λx.f (f (f x)))

giving,

λf.λx.f (λx.f (f (f x))) x)

The beta reduction is repeated again on the sub term λx.f (f (f x))) x. Here

x is replaced by x in f (f (f x)))

giving,

λf.λx.f (f (f (f x))))

The expression can no longer be reduced and is regarded as being a value in normal formal.

In Church numerals, λf.λx.f (f (f (f x)))) represents the number 5, because it applies the function f five times to the parameter x. This is an interpretation of the lambda term, but the term may also be regarded only as a function definition that cannot be further reduced.

As another example,

λx.((λf.λx.f (f x)) x)

This term cannot be reduced in the same way as the previous expression. But lambda calculus allows a second type of reduction called eta reduction. When a parameter λx is then used as a parameter to a sub term then they may both be eliminated, giving,

λf.λx.f (f x)

Each lambda abstractions defines a local variable, which is a placeholder which will be substituted with a value during beta reduction. The name is not regarded as important. Only the structure is important. So,

λf.λx.f (f x)

is regarded as being identical to,

λa.λb.a (a b)

Converting between the two forms is called alpha conversion.

There are some complications in the details of the naming of variables. As in other programming languages, the simple rule is that lambda terms behave as if each expression was parsed and every local variable renamed with a unique name.

The rules,

• Beta reduction
• Eta reduction
• Alpha conversion

described formally, define lambda calculus.

Lambda abstraction

In mathematics a function is defined in the form,

$f\ x=x^{2}$

Here I am using the functional notation $f\ x$ instead of $f(x)$ to represent the application of a function to a parameter. This is the notation for function application used in functional languages such as ML, Miranda and Haskell.

The lambda abstraction is conceived by considering what is the value of $f$. $f$ is a function, but what is it equal to? What is it's value? The lambda abstraction provides a notation for representing this value.

$f=\lambda x.x^{2}$

The lambda abstraction $\lambda x.x^{2}$ is also called an anonymous function, because it defines a function without giving it a name.

Problems with the Lambda Abstraction

The lambda abstraction is a definition. However defining something does not make it exist. Soon after discovering the lambda abstraction it was found to have inconsistencies when considered as a mathematical expression (see Kleene–Rosser paradox and Curry's Paradox).

The lambda abstraction was then used as the basis for a programming language, the Lambda Calculus. As a programming language the lambda calculus could not lean on mathematics as it's basis. Instead fundamental theorems about it's behavior had to be proved specifically for the lambda calculus.

Definition

Topic	Description
Standard definition	The formal definition, in the mathematical style originally given by Alonzo Church.
Syntax definition in Backus–Naur Form	Syntax of Lambda Calculus.
Definition as mathematical formulas	Gives a definition using mathematical formulas.
Derivation of standard definition	Derive standard definition from mathematical formulas.
Evaluation strategy	Defines the order of evaluation.

Topics

Topic	Description
Church encoding of data types	Builds representations of basic data type values, from which Turing completeness may be shown.
Mogensen–Scott encoding	An alternate system of encoding, based on abstract data types.
SKI combinator calculus	Basic operators, called combinators, that act to direct and control parameters, that may be put together to construct a language without named parameters.
Curry's paradoxical Y combinator	A lambda calculus function that implements recursion.
Lambda lifting	A method to transform functions so that local functions are moved into a global scope.
Anonymous function	A function defined without a name.
Böhm tree	A method of obtaining part of the "value" of the calculation, from a lambda term, before the calculation is complete.

Technical problems and paradoxes

Topic	Description
Curry's paradox	A paradox arising from the consideration of lambda calculus as a deductive system.
Kleene–Rosser paradox	A demonstration that some form of lambda calculus is inconsistent
Deductive lambda calculus	Describes the consequences of adding lambda abstractions as an extension to mathematics.

Important theorems

Topic	Description
Church–Rosser theorem	A lambda term will always reduce to the same normal for, regardless of the path of beta and eta-reductions.
Church–Turing thesis	Any computible function may be represented by a Turing machine, or equivalenty, a Lambda calculus program.
The undecidability of equivalence.	There is no program that will always tell if two functions are equal or not.
Curry–Howard correspondence	The direct relationship between computer programs and mathematical proofs.

Related languages

Topic	Description
Typed lambda calculus	Lambda calculus with typed variables (and functions)
Simply typed lambda calculus	Lambda calculus based on a simple theory of types, which is contradiction free.
Let expression	An expression close related to a lambda abstraction.

Standard terms

Encoding datatypes

Main articles: Church encoding and Mogensen–Scott encoding

Church Numerals

Function	Algebra	Identity	Function definition	Lambda expressions
Successor	$n+1$	$f^{n+1}\ x=f(f^{n}x)$	succ n f x=f (n f x)	λn.λf.λx.f (n f x)	...
Addition	$m+n$	$f^{m+n}\ x=f^{m}(f^{n}x)$	plus m n f x=m f (n f x)	λm.λn.λf.λx.m f (n f x)	λm.λn.n succ m
Multiplication	$m*n$	$f^{m*n}\ x=(f^{m})^{n}\ x$	multiply m n f x=m (n f) x	λm.λn.λf.λx.m (n f) x	λm.λn.λf.m (n f)
Exponentiation	$m^{n}$	$n\ m\ f=m^{n}\ f$	exp m n f x=(n m) f x	λm.λn.λf.λx.(n m) f x	λm.λn.n m
Predecessor*	$n-1$	$\operatorname {inc} ^{n}\operatorname {con} =\operatorname {val} (f^{n-1}x)$	pred ...	λn.λf.λx.n (λg.λh.h (g f)) (λu.x) (λu.u)
Subtraction*	$m-n$	$f^{m-n}\ x=(f^{-1})^{n}(f^{m}x)$	minus m n = (n pred) m	...	λm.λn.n pred m

divide = λn.((λf.(λx.x x) (λx.f (x x))) (λc.λn.λm.λf.λx.(λd.(λn.n (λx.(λa.λb.b)) (λa.λb.a)) d ((λf.λx.x) f x) (f (c d m f x))) ((λm.λn.n(λn.λf.λx.n (λg.λh.h (g f)) (λu.x) (λu.u))m) n m))) ((λn.λf.λx.f (n f x)) n)

Main articles: Fixed-point combinator and SKI combinator calculus

Booleans

Name	Definition
true	λa.λb.a
false	λa.λb.b
and	λp.λq.p q p
or	λp.λq.p q p
not1	λp.λa.λb.p b a
not2	λp.p (λa.λb.b) (λa.λb.a)
xor	λa.λb.a (not b) b
if	λp.λa.λb.p a b

Predicates

Name	Definition
IsZero	λn.n (λx.false) true
LEQ	λm.λn.IsZero (minus m n)
EQ	λm.λn.and (LEQ m n) (LEQ n m)

Pair

Name	Definition
pair	λx.λy.λz.z x y
first	λp.p (λx.λy.x)
second	λp.p (λx.λy.y)

Combinators

Main articles: Fixed-point combinator and SKI combinator calculus

Name	Definition
I	λx.x
K	λx.λy.x
S	λx.λy.λz.x z (y z)
B	λx.λy.λz.x (y z)
C	λx.λy.λz.x z y
W	λx.λy.x y y
U	λx.x x
ω	λx.x x
Ω	ω ω
Y	λg.(λx.g (x x)) (λx.g (x x))

Technical considerations

Computable functions and lambda calculus

A function F: N → N of natural numbers is a computable function if and only if there exists a lambda expression f such that for every pair of x, y in N, F(x)=y if and only if f x =_β y,  where x and y are the Church numerals corresponding to x and y, respectively and =_β meaning equivalence with beta reduction. This is one of the many ways to define computability; see the Church-Turing thesis for a discussion of other approaches and their equivalence.

Undecidability of equivalence

There is no algorithm that takes as input two lambda expressions and outputs TRUE or FALSE depending on whether or not the two expressions are equivalent. This was historically the first problem for which undecidability could be proven. As is common for a proof of undecidability, the proof shows that no computable function can decide the equivalence. Church's thesis is then invoked to show that no algorithm can do so.

Church's proof first reduces the problem to determining whether a given lambda expression has a normal form. A normal form is an equivalent expression that cannot be reduced any further under the rules imposed by the form. Then he assumes that this predicate is computable, and can hence be expressed in lambda calculus. Building on earlier work by Kleene and constructing a Gödel numbering for lambda expressions, he constructs a lambda expression e that closely follows the proof of Gödel's first incompleteness theorem. If e is applied to its own Gödel number, a contradiction results.

Normal forms and confluence

Main article: Normalization property (abstract rewriting)

For the untyped lambda calculus, β-reduction as a rewriting rule is neither strongly normalising nor weakly normalising.

However, it can be shown that β-reduction is confluent. (Of course, we are working up to α-conversion, i.e. we consider two normal forms to be equal, if it is possible to α-convert one into the other.)

Therefore, both strongly normalising terms and weakly normalising terms have a unique normal form. For strongly normalising terms, any reduction strategy is guaranteed to yield the normal form, whereas for weakly normalising terms, some reduction strategies may fail to find it.

Anonymous functions

Main article: Anonymous function

Lambda calculus reifies "functions" and makes them first-class objects, which raises implementation complexity when it is implemented.

For example in Lisp the 'square' function can be expressed as a lambda expression as follows:

(lambda (x) (* x x))

The above example is an expression that evaluates to a first-class function. The symbol lambda creates an anonymous function, given a list of parameter names, (x) — just a single argument in this case, and an expression that is evaluated as the body of the function, (* x x). The Haskell example is identical. Anonymous functions are sometimes called lambda expressions.

For example Pascal and many other imperative languages have long supported passing subprograms as arguments to other subprograms through the mechanism of function pointers. However, function pointers are not a sufficient condition for functions to be first class datatypes, because a function is a first class datatype if and only if new instances of the function can be created at run-time. And this run-time creation of functions is supported in Smalltalk, Javascript, and more recently in Scala, Eiffel ("agents"), C# ("delegates") and C++11, among others.

Semantics

The fact that lambda calculus terms act as functions on other lambda calculus terms, and even on themselves, led to questions about the semantics of the lambda calculus. Could a sensible meaning be assigned to lambda calculus terms? The natural semantics was to find a set D isomorphic to the function space D → D, of functions on itself. However, no nontrivial such D can exist, by cardinality constraints because the set of all functions from D to D has greater cardinality than D, unless D is a singleton set.

In the 1970s, Dana Scott showed that, if only continuous functions were considered, a set or domain D with the required property could be found, thus providing a model for the lambda calculus.

This work also formed the basis for the denotational semantics of programming languages.

See also

Topic	Description
Applicative computing systems	Treatment of objects in the style of the lambda calculus
Binary lambda calculus	A version of lambda calculus with binary I/O, a binary encoding of terms, and a designated universal machine.
Calculus of constructions	A typed lambda calculus with types as first-class values
Cartesian closed category	A setting for lambda calculus in category theory
Categorical abstract machine	A model of computation applicable to lambda calculus
Combinatory logic	A notation for mathematical logic without variables
Curry–Howard isomorphism	The formal correspondence between programs and proofs
Domain theory	Study of certain posets giving denotational semantics for lambda calculus
Evaluation strategy	Rules for the evaluation of expressions in programming languages
Explicit substitution	The theory of substitution, as used in β-reduction
Harrop formula	A kind of constructive logical formula such that proofs are lambda terms
Kappa calculus	A first-order analogue of lambda calculus
Kleene–Rosser paradox	A demonstration that some form of lambda calculus is inconsistent
Lambda cube	A framework for some extensions of typed lambda calculus
Lambda-mu calculus	An extension of the lambda calculus for treating classical logic
Rewriting	Transformation of formulæ in formal systems
SECD machine	A virtual machine designed for the lambda calculus
Simply typed lambda calculus	Version(s) with a single type constructor
SKI combinator calculus	A computational system based on the S, K and I combinators
System F	A typed lambda calculus with type-variables
Universal Turing machine	A formal computing machine that is equivalent to lambda calculus
Unlambda	An esoteric functional programming language based on combinatory logic

Further reading

• Abelson, Harold & Gerald Jay Sussman. Structure and Interpretation of Computer Programs. The MIT Press. ISBN 0-262-51087-1.
• Hendrik Pieter Barendregt Introduction to Lambda Calculus.
• Henk Barendregt, The Impact of the Lambda Calculus in Logic and Computer Science. The Bulletin of Symbolic Logic, Volume 3, Number 2, June 1997.
• Barendregt, Hendrik Pieter, The Type Free Lambda Calculus pp1091–1132 of Handbook of Mathematical Logic, North-Holland (1977) ISBN 0-7204-2285-X
• Cardone and Hindley, 2006. History of Lambda-calculus and Combinatory Logic. In Gabbay and Woods (eds.), Handbook of the History of Logic, vol. 5. Elsevier.
• Church, Alonzo, An unsolvable problem of elementary number theory, American Journal of Mathematics, 58 (1936), pp. 345–363. This paper contains the proof that the equivalence of lambda expressions is in general not decidable.
• Alonzo Church, The Calculi of Lambda-Conversion (ISBN 978-0-691-08394-0)
• Kleene, Stephen, A theory of positive integers in formal logic, American Journal of Mathematics, 57 (1935), pp. 153–173 and 219–244. Contains the lambda calculus definitions of several familiar functions.
• Landin, Peter, A Correspondence Between ALGOL 60 and Church's Lambda-Notation, Communications of the ACM, vol. 8, no. 2 (1965), pages 89–101. Available from the ACM site. A classic paper highlighting the importance of lambda calculus as a basis for programming languages.
• Larson, Jim, An Introduction to Lambda Calculus and Scheme. A gentle introduction for programmers.
• Schalk, A. and Simmons, H. (2005) An introduction to λ-calculi and arithmetic with a decent selection of exercises. Notes for a course in the Mathematical Logic MSc at Manchester University.
• de Queiroz, Ruy J.G.B. (2008) On Reduction Rules, Meaning-as-Use and Proof-Theoretic Semantics. Studia Logica, 90(2):211-247. A paper giving a formal underpinning to the idea of 'meaning-is-use' which, even if based on proofs, it is different from proof-theoretic semantics as in the Dummett–Prawitz tradition since it takes reduction as the rules giving meaning.

Monographs/textbooks for graduate students:

• Morten Heine Sørensen, Paweł Urzyczyn, Lectures on the Curry-Howard isomorphism, Elsevier, 2006, ISBN 0-444-52077-5 is a recent monograph that covers the main topics of lambda calculus from the type-free variety, to most typed lambda calculi, including more recent developments like pure type systems and the lambda cube. It does not cover subtyping extensions.
• Pierce, Benjamin (2002), Types and Programming Languages, MIT Press, ISBN 0-262-16209-1 covers lambda calculi from a practical type system perspective; some topics like dependent types are only mentioned, but subtyping is an important topic.

Some parts of this article are based on material from FOLDOC, used with permission.

External links

• "Lambda-calculus", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Achim Jung, A Short Introduction to the Lambda Calculus-(PDF)
• Dana Scott, A timeline of lambda calculus-(PDF)
• David C. Keenan, To Dissect a Mockingbird: A Graphical Notation for the Lambda Calculus with Animated Reduction
• Raúl Rojas, A Tutorial Introduction to the Lambda Calculus-(PDF)
• Peter Selinger, Lecture Notes on the Lambda Calculus-(PDF)
• L. Allison, Some executable λ-calculus examples
• Georg P. Loczewski, The Lambda Calculus and A++
• Bret Victor, Alligator Eggs: A Puzzle Game Based on Lambda Calculus
• Lambda Calculus on Safalra’s Website
• "Lambda Calculus". PlanetMath.
• LCI Lambda Interpreter a simple yet powerful pure calculus interpreter
• Lambda Calculus links on Lambda-the-Ultimate
• Mike Thyer, Lambda Animator, a graphical Java applet demonstrating alternative reduction strategies.
• An Introduction to Lambda Calculus and Scheme, by Jim Larson
• Implementing the Lambda calculus using C++ Templates
• Marius Buliga, Graphic lambda calculus
• Lambda Calculus as a Workflow Model by Peter Kelly, Paul Coddington, and Andrew Wendelborn; mentions graph reduction as a common means of evaluating lambda expressions and discusses the applicability of lambda calculus for distributed computing (due to the Church–Rosser property, which enables parallel graph reduction for lambda expressions).
• Shane Steinert-Threlkeld, "Lambda Calculi", Internet Encyclopedia of Philosophy

References

Category:1936 in computing Category:American inventions Category:Articles with example code Category:Computability theory Category:Formal methods Category:Models of computation Category:Theoretical computer science