Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926.[1][2] Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.
Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi–Dirac statistics is most commonly applied to electrons, a type of fermion with spin 1/2.
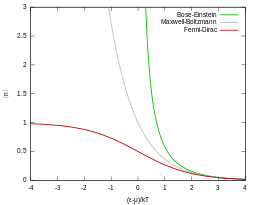
A counterpart to Fermi–Dirac statistics is Bose–Einstein statistics, which applies to identical and indistinguishable particles with integer spin (0, 1, 2, etc.) called bosons. In classical physics, Maxwell–Boltzmann statistics is used to describe particles that are identical and treated as distinguishable. For both Bose–Einstein and Maxwell–Boltzmann statistics, more than one particle can occupy the same state, unlike Fermi–Dirac statistics.
History edit
Before the introduction of Fermi–Dirac statistics in 1926, understanding some aspects of electron behavior was difficult due to seemingly contradictory phenomena. For example, the electronic heat capacity of a metal at room temperature seemed to come from 100 times fewer electrons than were in the electric current.[3] It was also difficult to understand why the emission currents generated by applying high electric fields to metals at room temperature were almost independent of temperature.
The difficulty encountered by the Drude model, the electronic theory of metals at that time, was due to considering that electrons were (according to classical statistics theory) all equivalent. In other words, it was believed that each electron contributed to the specific heat an amount on the order of the Boltzmann constant kB. This problem remained unsolved until the development of Fermi–Dirac statistics.
Fermi–Dirac statistics was first published in 1926 by Enrico Fermi[1] and Paul Dirac.[2] According to Max Born, Pascual Jordan developed in 1925 the same statistics, which he called Pauli statistics, but it was not published in a timely manner.[4][5][6] According to Dirac, it was first studied by Fermi, and Dirac called it "Fermi statistics" and the corresponding particles "fermions".[7]
Fermi–Dirac statistics was applied in 1926 by Ralph Fowler to describe the collapse of a star to a white dwarf.[8] In 1927 Arnold Sommerfeld applied it to electrons in metals and developed the free electron model,[9] and in 1928 Fowler and Lothar Nordheim applied it to field electron emission from metals.[10] Fermi–Dirac statistics continues to be an important part of physics.
Fermi–Dirac distribution edit
For a system of identical fermions in thermodynamic equilibrium, the average number of fermions in a single-particle state i is given by the Fermi–Dirac (F–D) distribution,[11][nb 1]
where kB is the Boltzmann constant, T is the absolute temperature, εi is the energy of the single-particle state i, and μ is the total chemical potential. The distribution is normalized by the condition
that can be used to express in that can assume either a positive or negative value.[12]
At zero absolute temperature, μ is equal to the Fermi energy plus the potential energy per fermion, provided it is in a neighbourhood of positive spectral density. In the case of a spectral gap, such as for electrons in a semiconductor, the point of symmetry μ is typically called the Fermi level or—for electrons—the electrochemical potential, and will be located in the middle of the gap.[13][14]
The Fermi–Dirac distribution is only valid if the number of fermions in the system is large enough so that adding one more fermion to the system has negligible effect on μ.[15] Since the Fermi–Dirac distribution was derived using the Pauli exclusion principle, which allows at most one fermion to occupy each possible state, a result is that .[nb 2]
- Fermi–Dirac distribution
-
Temperature dependence for .
The variance of the number of particles in state i can be calculated from the above expression for ,[17][18]
Distribution of particles over energy edit
From the Fermi–Dirac distribution of particles over states, one can find the distribution of particles over energy.[nb 3] The average number of fermions with energy can be found by multiplying the Fermi–Dirac distribution by the degeneracy (i.e. the number of states with energy ),[19]
When , it is possible that , since there is more than one state that can be occupied by fermions with the same energy .
When a quasi-continuum of energies has an associated density of states (i.e. the number of states per unit energy range per unit volume[20]), the average number of fermions per unit energy range per unit volume is
where is called the Fermi function and is the same function that is used for the Fermi–Dirac distribution ,[21]
so that
Quantum and classical regimes edit
The Fermi–Dirac distribution approaches the Maxwell–Boltzmann distribution in the limit of high temperature and low particle density, without the need for any ad hoc assumptions:
- In the limit of low particle density, , therefore or equivalently . In that case, , which is the result from Maxwell-Boltzmann statistics.
- In the limit of high temperature, the particles are distributed over a large range of energy values, therefore the occupancy on each state (especially the high energy ones with ) is again very small, . This again reduces to Maxwell-Boltzmann statistics.
The classical regime, where Maxwell–Boltzmann statistics can be used as an approximation to Fermi–Dirac statistics, is found by considering the situation that is far from the limit imposed by the Heisenberg uncertainty principle for a particle's position and momentum. For example, in physics of semiconductor, when the density of states of conduction band is much higher than the doping concentration, the energy gap between conduction band and fermi level could be calculated using Maxwell-Boltzmann statistics. Otherwise, if the doping concentration is not negligible compared to density of states of conduction band, the Fermi–Dirac distribution should be used instead for accurate calculation. It can then be shown that the classical situation prevails when the concentration of particles corresponds to an average interparticle separation that is much greater than the average de Broglie wavelength of the particles:[22]
where h is the Planck constant, and m is the mass of a particle.
For the case of conduction electrons in a typical metal at T = 300 K (i.e. approximately room temperature), the system is far from the classical regime because . This is due to the small mass of the electron and the high concentration (i.e. small ) of conduction electrons in the metal. Thus Fermi–Dirac statistics is needed for conduction electrons in a typical metal.[22]
Another example of a system that is not in the classical regime is the system that consists of the electrons of a star that has collapsed to a white dwarf. Although the temperature of white dwarf is high (typically T = 10000 K on its surface[23]), its high electron concentration and the small mass of each electron precludes using a classical approximation, and again Fermi–Dirac statistics is required.[8]
Derivations edit
Grand canonical ensemble edit
The Fermi–Dirac distribution, which applies only to a quantum system of non-interacting fermions, is easily derived from the grand canonical ensemble.[24] In this ensemble, the system is able to exchange energy and exchange particles with a reservoir (temperature T and chemical potential μ fixed by the reservoir).
Due to the non-interacting quality, each available single-particle level (with energy level ϵ) forms a separate thermodynamic system in contact with the reservoir. In other words, each single-particle level is a separate, tiny grand canonical ensemble. By the Pauli exclusion principle, there are only two possible microstates for the single-particle level: no particle (energy E = 0), or one particle (energy E = ε). The resulting partition function for that single-particle level therefore has just two terms:
and the average particle number for that single-particle level substate is given by
This result applies for each single-particle level, and thus gives the Fermi–Dirac distribution for the entire state of the system.[24]
The variance in particle number (due to thermal fluctuations) may also be derived (the particle number has a simple Bernoulli distribution):
This quantity is important in transport phenomena such as the Mott relations for electrical conductivity and thermoelectric coefficient for an electron gas,[25] where the ability of an energy level to contribute to transport phenomena is proportional to .
Canonical ensemble edit
It is also possible to derive Fermi–Dirac statistics in the canonical ensemble. Consider a many-particle system composed of N identical fermions that have negligible mutual interaction and are in thermal equilibrium.[15] Since there is negligible interaction between the fermions, the energy of a state of the many-particle system can be expressed as a sum of single-particle energies,
where is called the occupancy number and is the number of particles in the single-particle state with energy . The summation is over all possible single-particle states .
The probability that the many-particle system is in the state , is given by the normalized canonical distribution,[26]
where , e is called the Boltzmann factor, and the summation is over all possible states of the many-particle system. The average value for an occupancy number is[26]
Note that the state of the many-particle system can be specified by the particle occupancy of the single-particle states, i.e. by specifying so that
and the equation for becomes
where the summation is over all combinations of values of which obey the Pauli exclusion principle, and = 0 or 1 for each . Furthermore, each combination of values of satisfies the constraint that the total number of particles is ,
Rearranging the summations,
where the on the summation sign indicates that the sum is not over and is subject to the constraint that the total number of particles associated with the summation is . Note that still depends on through the constraint, since in one case and is evaluated with while in the other case and is evaluated with To simplify the notation and to clearly indicate that still depends on through , define
so that the previous expression for can be rewritten and evaluated in terms of the ,
The following approximation[27] will be used to find an expression to substitute for .
where
If the number of particles is large enough so that the change in the chemical potential is very small when a particle is added to the system, then [28] Taking the base e antilog[29] of both sides, substituting for , and rearranging,
Substituting the above into the equation for , and using a previous definition of to substitute for , results in the Fermi–Dirac distribution.
Like the Maxwell–Boltzmann distribution and the Bose–Einstein distribution the Fermi–Dirac distribution can also be derived by the Darwin–Fowler method of mean values.[30]
Microcanonical ensemble edit
A result can be achieved by directly analyzing the multiplicities of the system and using Lagrange multipliers.[31]
Suppose we have a number of energy levels, labeled by index i, each level having energy εi and containing a total of ni particles. Suppose each level contains gi distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta (i.e. their momenta may be along different directions), in which case they are distinguishable from each other, yet they can still have the same energy. The value of gi associated with level i is called the "degeneracy" of that energy level. The Pauli exclusion principle states that only one fermion can occupy any such sublevel.
The number of ways of distributing ni indistinguishable particles among the gi sublevels of an energy level, with a maximum of one particle per sublevel, is given by the binomial coefficient, using its combinatorial interpretation
For example, distributing two particles in three sublevels will give population numbers of 110, 101, or 011 for a total of three ways which equals 3!/(2!1!).
The number of ways that a set of occupation numbers ni can be realized is the product of the ways that each individual energy level can be populated:
Following the same procedure used in deriving the Maxwell–Boltzmann statistics, we wish to find the set of ni for which W is maximized, subject to the constraint that there be a fixed number of particles, and a fixed energy. We constrain our solution using Lagrange multipliers forming the function:
Using Stirling's approximation for the factorials, taking the derivative with respect to ni, setting the result to zero, and solving for ni yields the Fermi–Dirac population numbers:
By a process similar to that outlined in the Maxwell–Boltzmann statistics article, it can be shown thermodynamically that and , so that finally, the probability that a state will be occupied is:
See also edit
Notes edit
- ^ The F-D Distribution is a type of mathematical function called a logistic function or sigmoid function.
- ^ Note that is also the probability that the state is occupied, since no more than one fermion can occupy the same state at the same time and .
- ^ These distributions over energies, rather than states, are sometimes called the Fermi–Dirac distribution too, but that terminology will not be used in this article.
References edit
- ^ a b Fermi, Enrico (1926). "Sulla quantizzazione del gas perfetto monoatomico". Rendiconti Lincei (in Italian). 3: 145–9., translated as Zannoni, Alberto (1999-12-14). "On the Quantization of the Monoatomic Ideal Gas". arXiv:cond-mat/9912229.
- ^ a b Dirac, Paul A. M. (1926). "On the Theory of Quantum Mechanics". Proceedings of the Royal Society A. 112 (762): 661–77. Bibcode:1926RSPSA.112..661D. doi:10.1098/rspa.1926.0133. JSTOR 94692.
- ^ (Kittel 1971, pp. 249–50)
- ^ "History of Science: The Puzzle of the Bohr–Heisenberg Copenhagen Meeting". Science-Week. 4 (20). 2000-05-19. OCLC 43626035. Archived from the original on 2009-04-11. Retrieved 2009-01-20.
- ^ Schücking (1999). "Jordan, Pauli, Politics, Brecht and a variable gravitational constant". Physics Today. 52 (10): 26. Bibcode:1999PhT....52j..26S. doi:10.1063/1.882858.
- ^ Ehlers; Schücking (2002). "Aber Jordan war der Erste". Physik Journal (in German). 1 (11): 71–72. hdl:11858/00-001M-0000-0013-5513-D.
- ^ Dirac, Paul A. M. (1967). Principles of Quantum Mechanics (revised 4th ed.). London: Oxford University Press. pp. 210–1. ISBN 978-0-19-852011-5.
- ^ a b Fowler, Ralph H. (December 1926). "On dense matter". Monthly Notices of the Royal Astronomical Society. 87 (2): 114–22. Bibcode:1926MNRAS..87..114F. doi:10.1093/mnras/87.2.114.
- ^ Sommerfeld, Arnold (1927-10-14). "Zur Elektronentheorie der Metalle" [On Electron Theory of Metals]. Naturwissenschaften (in German). 15 (41): 824–32. Bibcode:1927NW.....15..825S. doi:10.1007/BF01505083. S2CID 39403393.
- ^ Fowler, Ralph H.; Nordheim, Lothar W. (1928-05-01). "Electron Emission in Intense Electric Fields". Proceedings of the Royal Society A. 119 (781): 173–81. Bibcode:1928RSPSA.119..173F. doi:10.1098/rspa.1928.0091. JSTOR 95023.
- ^ (Reif 1965, p. 341)
- ^ Landau, L. D., & Lifshitz, E. M. (2013). Statistical Physics: Volume 5 (Vol. 5). Elsevier.
- ^ (Blakemore 2002, p. 11)
- ^ Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). San Francisco: W. H. Freeman. p. 357. ISBN 978-0-7167-1088-2.
- ^ a b (Reif 1965, pp. 340–342)
- ^ (Kittel 1971, p. 245, Figs. 4 and 5)
- ^ Pearsall, Thomas (2020). Quantum Photonics, 2nd edition. Graduate Texts in Physics. Springer. doi:10.1007/978-3-030-47325-9. ISBN 978-3-030-47324-2.
- ^ (Reif 1965, p. 351) Eq. 9.7.7 where .
- ^ Leighton, Robert B. (1959). Principles of Modern Physics. McGraw-Hill. p. 340. ISBN 978-0-07-037130-9. Note that in Eq. (1), and correspond respectively to and in this article. See also Eq. (32) on p. 339.
- ^ (Blakemore 2002, p. 8)
- ^ (Reif 1965, p. 389)
- ^ a b (Reif 1965, pp. 246–8)
- ^ Mukai, Koji; Jim Lochner (1997). "Ask an Astrophysicist". NASA's Imagine the Universe. NASA Goddard Space Flight Center. Archived from the original on 2009-01-18.
- ^ a b Srivastava, R. K.; Ashok, J. (2005). "Chapter 6". Statistical Mechanics. New Delhi: PHI Learning Pvt. Ltd. ISBN 9788120327825.
- ^ Cutler, M.; Mott, N. (1969). "Observation of Anderson Localization in an Electron Gas". Physical Review. 181 (3): 1336. Bibcode:1969PhRv..181.1336C. doi:10.1103/PhysRev.181.1336.
- ^ a b (Reif 1965, pp. 203–6)
- ^ See for example, Derivative - Definition via difference quotients, which gives the approximation f(a+h) ≈ f(a) + f '(a) h .
- ^ (Reif 1965, pp. 341–2) See Eq. 9.3.17 and Remark concerning the validity of the approximation.
- ^ By definition, the base e antilog of A is eA.
- ^ Müller-Kirsten, H. J. W. (2013). Basics of Statistical Physics (2nd ed.). World Scientific. ISBN 978-981-4449-53-3.
- ^ (Blakemore 2002, pp. 343–5)
Further reading edit
- Reif, F. (1965). Fundamentals of Statistical and Thermal Physics. McGraw–Hill. ISBN 978-0-07-051800-1.
- Blakemore, J. S. (2002). Semiconductor Statistics. Dover. ISBN 978-0-486-49502-6.
- Kittel, Charles (1971). Introduction to Solid State Physics (4th ed.). New York: John Wiley & Sons. ISBN 978-0-471-14286-7. OCLC 300039591.